Energie : saut à l'élastique, énergie nucléaire ( plutonium), énergie électrique ( dipôle LC) concours kiné AP HP 2009.

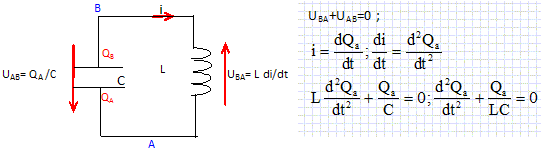
Saut à l'élastique. Les vecteurs sont écrits en gras et en bleu. Lors d'un saut à l'élastique, un candidats aux frissons, de masse m, s'élance d'un pont situé à une hauteur h au dessus du sol. L'élastique de masse négligeable se comporte comme un ressort de longueur à vide l0 = 0,25 h et de constante de raideur k. Une des extrémités de l'élastique est accrochée au pont et l'autre extrémité est accrochée au sauteur. On admettra que le mouvement s'effectue selon la verticale et on suppose que les frottements sont négligeables. On considère un axe verticale Oy orienté vers le haut et dont l'origine est située au niveau du sol. On notera u le vecteur unitaire lié à l'axe Oy et g l'intensité de la pesanteur. La position du sauteur assimilé à son centre d'inertie est repérée par sa distance au sol y. On posera l'énergie potentielle de pesanteur nulle au sol et l'énergie potentielle élastique nulle pour l'élastique à vide. Faire le bilan des forces subies par le sauteur. - élastique non tendu : poids P = mg (-u) verticale vers le bas, valeur mg - élastique tendu : poids verticale vers le bas, valeur mg et tension de l'élastique de la forme T = k (L-L0)u, avec L0 = 0,25 h et L = h-y :T = k (0,75h-y)u. Etablir l'expression donnant la résultante des forces en fonction de m, k, g, y et u, lorsque le sauteur est à une altitude comprise entre y = 0 et y = 0,75 h. P + T = mg (-u) + k (0,75h-y)u. Donner l'expression de l'énergie potentielle élastique Ep élas pour une altitude y comprise entre y = 0 et y = 0,75 h. Ep élas= ½k(L-L0)2 = ½ k (0,75h-y)2. En déduire l'expression donnant l'énergie potentielle du système à cette même altitude. Ep=½ k (0,75h-y)2 + mgy. En supposant que la vitesse initiale du sauteur soit nulle, au delà de quelle valeur de la constante de raideur k, le saut est-il sans danger, c'est à dire que le sauteur touche le sol avec une vitesse nulle ? L'énérgie mécanique initiale du système { élastique sauteur} est sous forme potentielle de pesanteur : E = mgh. L'énergie mécanique finale est sous forme potentielle élastique E = ½ k (0,75h-y)2 avec y = 0 soit E = ½ k (0,75h)2 Conservation de l'énergie mécanique : mgh = ½ k (0,75h)2 ; k = 2mgh / (0,75h)2 = 32 mg / (9h). Le saut est sans danger si k est supérieur ou égale à : 32 mg / (9h). A.N : m = 90 kg ; g = 10 m s-2 ; h = 100 m. k = 32*90*10/(900) = 32 N m-1. Energie nucléaire. Certains appareils utilisés en médecine utilisent du plutonium 23894Pu qui se désintègre en émettant une particule alpha d'énergie cinétique Ec(a) = 12 MeV. La demi-vie du plutonium 238 est t½ = 5,6 109 s. La source contenant une masse m = 29,75 mg de plutonium 238 est scellée hermétiquement dans un récipient, l'énergie étant alors transformée en énergie thermique. On donne : NA = 6,0 1023 mol-1 ; c = 3,0 108 m/s ; h = 6,4 10-34 J s ; ln 2 = 0,70 ; ln5 = 1,6 ; ln7,= 2,0 ; 1 MeV = 1,6 10-13 J.  Quelles sont les grandeurs physiques conservées lors de la désintégration du plutonium 238 ? Conservation de la charge ; conservation du nombre de nucléons. Ecrire l'équation de désintégration du plutonium 238. Préciser le nombre de neutrons du noyau fils. 23894Pu ---> 23492U + 42He Le noyau fils compte 234-92 = 142 neutrons. Les énergies de liaison par nucléon sont notées El(Pu), El(a), El(AZX). Etablir l'expression de l'énergie libérée lors de la désintégration en fonction des énergies de liaison par nucléon. E = 4El(a) + 234El(AZX) -238El(Pu). Donner l'expression du nombre d'atomes de plutonium initialement présents dans la source utilisée. Faire l'application numérique. N = m/M * NA avec M masse molaire du plutonium 238. N = 29,75 10-3 /238 *6,0 1023 =7,5 1019 atomes. Donner l'expression de la puissance thermique initiale Pth0 puis calculer sa valeur. Chaque atome est susceptible de se désintégrer en libérant une particule alpha et en libérant une énergie de 12 MeV. Ec(a) =12 MeV = 12*1,6 10-13 J. Constante radioactive : l = ln 2 / t½ ; activité initiale A0 = lN0 = ln 2 / t½ N0. L'activité est le nombre de désintégrations par seconde ; la puissance de la source est l'énergie libérée par seconde. Pth0 = ln 2 / t½ N0 Ec(a). Pth0 =ln2 / (5,6 109) *7,5 1019 *12*1,6 10-13 =0,7/5,6*7,5*12*1,6 10-3 =1,8 10-2 W.   La source assure la conversion d'énergie thermique en énergie électrique. la puissance électrique initiale obtenue est P = 180 µW. Exprimer puis calculer le rendement de la conversion. rendement = P / Pth0 =1,80 10-4 / 1,8 10-2 =0,01 ( 1 %) La pile fonctionne de façon correcte tant que sa perte de puissance reste inférieure à 30% de sa puissance initiale. Exprimer puis calculer la durée pendant laquelle la source peut fonctionner de façon correcte. La puissance de la source à la date t est proportionnelle au nombre de noyaux présents à cette date. P(t) =constante * N = constante *N0 exp(-lt) ; P(t=0) = constante *N0 =Pth0 P(t) = Pth0exp(-lt) 0,7 Pth0 = Pth0exp(-lt) ; 0,7 = exp(-lt) ; t = -ln0,7 / l ; t = -ln0,7 *t½ / ln2. t = -5,6 109 / 0,7 ln 0,7 = -8 109 (ln (7/10)) = -8 109 (ln 7-ln2-ln5)= -8 109(2-0,7-1,6) = 2,4 109 s. La désintégration du plutonium 238 s'accompagne d'émission de photons, chacun d'énergie E = 1,5 MeV. Calculer la longueur d'onde des photons émis. l = hc/E = 6,4 10-34 * 3,0 108 / (1,5*1,6 10-13) =6,4*3/(1,5*1,6) 10-13 =4/0,5 10-13 =8 10-13 m. Energie électrique : On considère un circuit électrique formé d'un condensateur de capacité C =25 µF, d'une bobine d'inductance L = 40 mH, de résistance nulle et d'un interrupteur. A l'instant t=0 on ferme l'interrupteur, le condensateur possédant alors une énergie de 50 µJ. On prendra pi ~ 3. Comment nomme t-on ce type d'oscillateur ? Dipôle (LC) non amorti ( oscillateur harmonique) Donner l'expression de la période et calculer sa valeur. T = 2 pi (LC)½ = 6(4 10-2 *25 10-6)½ = 6 10-3 s. Exprimer puis calculer la tension initiale U0 aux bornes du condensateur. énergie stockée par le condensateur e =½CU20 ; U0 = (2E/C)½ =(100 10-6 / 25 10-6) =2 V. Etablir l'équation différentielle régissant l'évolution de la charge d'un armature du condensateur au cours du temps. La solution de cette équation différentielle est de la forme q(t) = A cos (wt+f). Donner les expression de A, w et f en justifiant. w = (LC)-½ = (4 10-2 * 25 10-6)-½ = 103 rad/s. q(0) = A cos f avec E = ½q2(0) / C ; q(0) = + (2EC)½ ou q(0) = - (2EC)½ Dans l'hypothèse q(0) = + (2EC)½ : f = 0 et A = (2EC)½ = (2*50 10-6 *25 10-6)½=50 10-6 C = 5 10-5 C. q(t) = 5 10-5 cos (1000t). Etablir l'expression Wel(t) de l'énergie stockée dans le condensateur au cours du temps. Wel(t) = ½q2(t) / C = E cos2(wt) avec E = 50µJ. Wel(t) = 50 cos2(wt) en µJ. Donner l'allure de la courbe donnant l'évolution de Wel(t) sur deux périodes. Etablir l'expression Wmag(t) de l'énergie stockée dans la bobine au cours du temps. 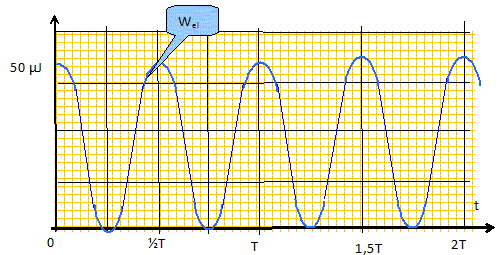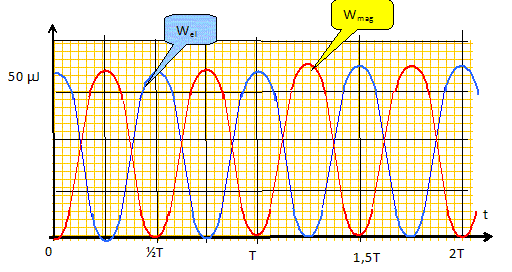Wmag(t)+ Wel(t) = E = 50 µJ= constante. Wmag(t) =E-Wel(t) =E ( 1 -cos2(wt) en µJ. ou bien Wmag(t) = ½Li2(t) avec i(t) = dq/dt =-(2EC)½ wsin(wt) Wmag(t) =LC Ew2sin2(wt) = E sin2(wt). Donner l'allure de la courbe donnant l'évolution de Wmag(t) sur deux périodes. En réalité la bobine n'est pas idéale. Par un bilan de puissance, établir l'équation différentielle régissant l'évolution de la charge au cours du temps. Puissance électrique mise en jeu par le condensateur : dWel /dt = q(t) / C q'(t) Puissance magnétique mise en jeu par la bobine : dWmag /dt = L i(t) i'(t)= L q'(t) q"(t) Puissance perdue par effet Joule dans les parties résistives : -r i2(t) = -r q'(t)2. Bilan : dWel /dt + dWmag /dt = - r i2(t) q(t) / C q'(t) + L q'(t) q"(t) = - rq'(t)2. q(t) / C+Lq"(t) = -r q'(t) ; q"(t) + r/L q'(t) + q(t) / (LC) =0.

c

retour -menu