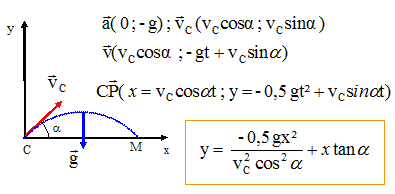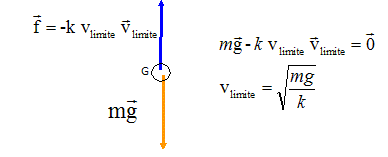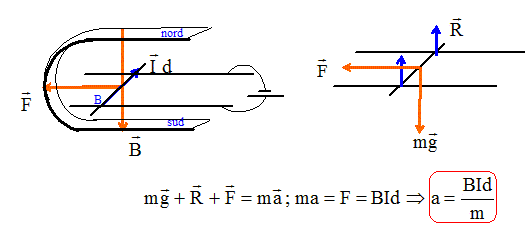accélération, chute libre, chute avec frottement, 3è loi de Kepler, pendule, force de Laplace concours kiné 2009.

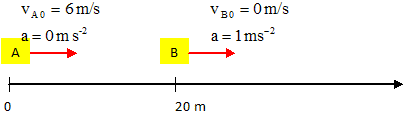
Distance entre A et B. Analyse : mouvement de A. rectiligne uniforme xA = vA 0 t = 6 t. Analyse : mouvement de B. rectiligne uniformément accéléré : xB = ½at2 +20 = 0,5 t2 +20 Analyse : distance minimale AB. xB - xA = 0,5 t2 -6t + 20 La distance sera minimale si la dérivée est nulle : t-6 = 0 soit t = 6 s. xB - xA =0,5*62 - 6*6 +20 = 2 m. ( B) proton dans un champ magnétique uniforme. 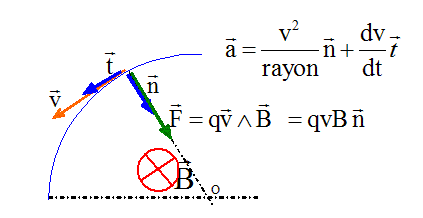Analyse : nature du mouvement. La force est à chaque instant perpendiculaire à la vitesse : cette force ne travaille pas et en conséquence ne modifie pas l'énergie cinétique. La vitesse de la particule chargée garde une valeur constante : mouvement uniforme. La force est constante et est centripète : mouvement circulaire. ( C) Chute libre. Analyse : sommet de la trajectoire. Au sommet de la trajectoire, la vitesse est horizontale : la composante verticale de la vitesse est nulle. -gt + vC sin q = 0 ; t = vC sin q / g. A.N : vC = 10 m/s ; g = 10 m s-2 ; sin q =0,125 ; t = 0,125 s~0,13 s. (B) Chute verticale avec frottements : Analyse : vitesse limite. Lorsque la vitesse limite est atteinte, le mouvement est rectiligne uniforme. D'après le principe d'inertie, la somme vectorielle des forces est nulle. A.N : m = 40 g =0,040 kg ; g = 10 m s-2 ; k = 4,0 10-3 S.I ; vlimite = [ 0,04*10/4,0 10-3]½= 10 m / s. 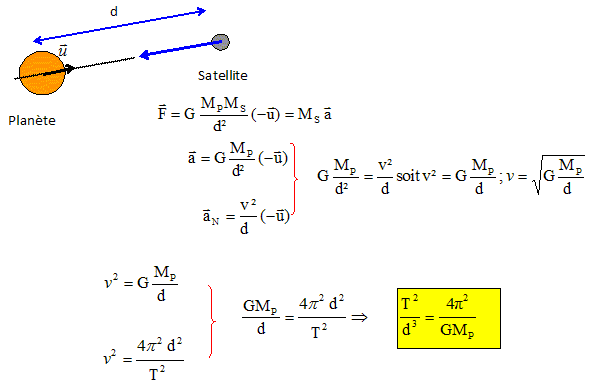(A) Satellite en orbite circulaire : Analyse : masse de la planète. Par rapport à un référentiel planètocentrique galiléen : - la connaissance de l'accélération et du rayon de l'orbite circulaire permet de calculer la masse de la planète - la connaissance de la période de révolution et du rayon de l'orbite circulaire permet de calculer la masse de la planète. 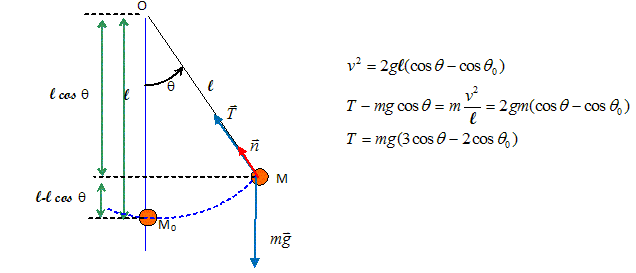(E) pendule simple : Analyse : tension du fil en M0. A la position M0, l'angle q est nu, cos q = 1 d'où T =mg(3-2 cosq0). (E) Oscillateur horizontal. Abscisse x(t) = xmax cos ( 2pf t) Vitesse, dérivée de l'abscisse par rapport au temps : v(t) = xmax (-2pf )sin ( 2pf t) Accélération, dérivée de la vitesse par rapport au temps : a(t) = -xmax (2pf )2 cos ( 2pf t) Valeur maximale de l'accélération : xmax (2pf )2 A.N : xmax =0,052 m ; f = 0,21 Hz ; a = 0,05 *(6,28*0,21) = 0,090 m s-2. (B)  Force de Laplace. A.N : m = 25 g ; B = 0,25 T ; I = 8,0 A ; d = 12,5 cm a = 0,25*8*0,125/0,025 = 10 m s-2. (D) Théorème de l'énergie cinétique. Analyse : entre O et A. Le poids et l'action du plan perpendiculaires à la vitesse ne travaillent pas. W = OA ( F-f) = 100F -6500. Variation de l'énergie cinétique : ½mvA2-0 = OA ( F-f) Analyse : entre A et B. L'action du plan perpendiculaire à la vitesse ne travaillent pas. Travail résistant du poids en montée :Wpoids = -2*mg = - 800 J. Variation de l'énergie cinétique : ½mvB2-½mvA2 = -800. ½mvA2 =½mvB2+800 =20*23,72 +800=12 103 J. Analyse : valeur de F. 12 103 = 100F -6500. F = (12 103 +6500) / 100 = 185 N. (C) Distance de freinage. 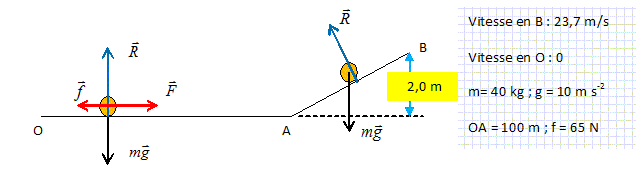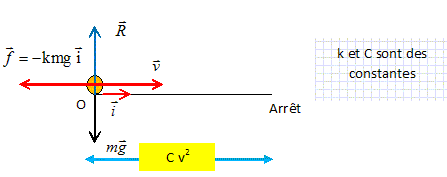Ecrire le théorème de l'énergie cinétique entre O et le point d'arrêt. Le poids et l'action du plan perpendiculaires à la vitesse ne travaillent pas. Travail résistant de la force de freinage f : Wf = -kmg Cv2. Variation de l'énergie cinétique : 0-½mv2. kmg Cv2 = ½mv2 ; kCg=½ ; C = 1 / (2kg). (E) Masse volumique du noyau d'un atome. R = A1/3 avec A ; nombre de nucléons et R rayon du noyau en fm ( 10-15 m) Masse d'un nucléon : m = 2 10-27 kg. masse du noyau : M= A m (kg) volume du noyau supposé sphérique : 4/3 *3,14 (10-15R)3 = 4/3 *3,14 10-45 A (m3) masse volumique : M/V = 2 10-27 *3 / (4*3,14 10-45) ~5 1017 kg m-3. (D)

c

retour -menu