|
Relèvement d'un virage, RLC triphasé, hydraulique : Venturi (ingénieur territotial 2009)
|
|||||||
|
|||||||
|
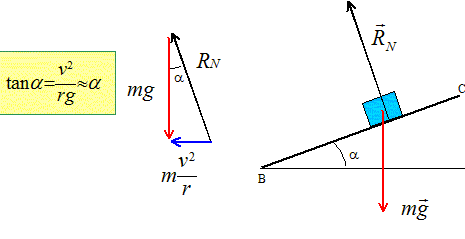
Un train est composé de deux motrices de 34 tonnes chacune et de trois voitures remorquées de 24 tonnes chacune. Chaque motrice développe une puissance de 260 kW chacune. Le démarrage sur voie horizontale rectiligne utilise 80 % de la puissance totale reçue par le train et s'effectue en 20 secondes Calculer la vitesse ( en km/h) atteinte par le train. Energie acquise par le train = 0,8 * puissance * durée E = 0,8*2*260 103*20 =8,32 106 J Cette énergie se retrouve sous forme cinétique : ½mv2 avec m = 34*2+3*24 = 140 t = 1,4 105 kg. v2 = 2*8,32 106 / 1,4 105 =118,9 ; v = 10,9 m/s = 10,9*3,6 km/h = 39,2 km/h. Calculer l'accélération supposée constante au cours du démarrage. a = Dv / D t =10,9/20 = 0,545 ~0,55 m s-2. La vitesse précédente étant maintenue, le train négocie une courbe de 712 m de rayon. Déterminer l'angle que fait le plan de la voie ferrée avec le plan horizontal pour que le virage soit entièrement sécurisé. Effectuer le schéma des forces appliquées au centre de gravité dans le plan vertical ( g = 9,81 m s-2).
En déduire la hauteur approximative dont est surélévé l'un des rails par rapport à l'autre, la largeur de la voie étant 1,44 m. Soit a l'inclinaison du plan des rails par rapport à l'horizontale ; cet angle étant faible on peut utiliser l'approximation suivante tan a =sin a. sin a = h / 1,44 ; h = 1,44 sin 0,97 = 0,025 m = 2,4 cm. Electricité : RLC triphasé.
On soumet une bobine ( résistance R, inductance L) à une tension continue de 120 V. Le courant qui la traverse a pour intensité I=3 A. Si on soumet cette bobine a une tension alternative sinusoïdale ( 230 V- 50 Hz) le courant qui la traverse a pour intensité efficace 2,875 A. En déduire les valeurs de la résistance R, de l'impédance réelle Z, de l'inductance L et du déphasage de l'intensité par rapport à la tension aux bornes de la bobine. En courant continu la bobine se comporte comme un conducteur ohmique : R= U/I = 120/3 = 40 W. En courant alternatif, l'impédance vaut : Z = (R2+(Lw)2)½ avec w = 2*3,14*50 = 314 rad/s. de plus Z = Ueff / Ieff = 230 / 2,875 =80 W. Inductance : R2+(Lw)2 = Z2 ; (Lw)2 = Z2 -R2 = 802-402 =4800 ; Lw = 69,28 ; L = 69,28/314 = 0,22 H. Déphasage : l'intensité est en retard sur la tension d'un angle j tel que tan j = Lw/R = 69,28/40 =1,732 ; j = -60°.
Le courant qui la traverse a toujours pour intensité efficace 2,875 A. En déduire l'impédance réelle du condensateur et la valeur C de sa capacité. Impédance Z de l'ensemble : 230 / 2,875 = 80 W. Impédance complexe de l'ensemble : Z = R + j(Lw -1/(Cw)) module de Z = impédance réelle Z = [R2 + (Lw -1/(Cw))2]½ = 80 W. Or [R2 + (Lw)2]½ = 80 W. R2 + (Lw -1/(Cw))2 = R2 + (Lw)2 ; (Lw -1/(Cw))2 =(Lw)2 ; Lw -1/(Cw) = + Lw et Lw -1/(Cw) = - Lw soit 1/(Cw) = 2 Lw. Impédance du condensateur : 2 Lw = 2*69,28 = 138,56 ~139 W. Capacité : C = 1/(138,56*314) =2,3 10-5 F.
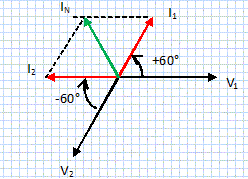
A l'aide de la représentation de Fresnel, déterminer la valeur efficace de l'intensité dans le neutre. Impédance de la branche R' condensateur en série : Z = (402+69,282)½= 80,44 W. Intensité efficace I1 eff = 230/80,44 =2,86 A Déphasage : intensité en avance sur la tension tan j '= 69,28/40 =1,732 ; j '=+60°.
Intensité efficace dans le neutre : 2,86 A.
|
|||||||
|
|