Pendule de Pohl: oscillations forcées concours physique ITPE 2009.

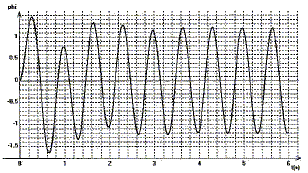
Un pendule de Pohl est constitué : - D'un disque en rotation autour de son centre. - D'un ressort spiral, qui exerce un couple mécanique qui tend à ramener le disque vers sa position d'équilibre. - D'un pointeur placé sur le disque qui permet de repérer les écarts angulaires. - D'un moteur, relié au ressort spiral, qui forcer les oscillations à une fréquence ajustable par l'utilisateur. - D'un frein électromagnétique, permettant de régler l'effet d'amortissement (par courants de Foucault). La position du disque résonateur est repéré par l'angle j(t). Le ressort spiral a une extrémité soudée en O, point fixe., l'autre extrémité mobile soudée en A au bras excitateur de position je. Le bras excitateur peut être mis en mouvement sinusoïdal de fréquence f par un moteur pas-à-pas avec une bielle. - Si je = cste, régime libre. Le moteur est étteint. - Si je = Fe cos (wt), régime forcé. Le moteur est en rotation à la fréquence f. Le disque résonateur passe dans l'entrefer d'un système magnétique alimenté par une intensité I : une force de freinage dite de Foucault est induite sur le disque résonateur. Mise en équation. L'équation de la position du disque peut se mettre sous la forme : j'' + 2 xw0j' +w02j = w02je.(1) Le système est immobile et on met en route le moteur pas à pas qui crée une excitation sinusoïdale je= Fe. cos ( wt) Décrire ce que l'on observe sur la courbe j (t) ci-dessous. A partir de t = 2,6 s, on observe un régime sinusoïdal forcé ; de t=0 à t = 2,6 s, le régime est transitoire. Par la suite, on prendra j (t) =F cos (wt+a). On notera j =F exp (ja) tel que j (t) = Re ( j exp( jwt)) Déterminer j en fonction de Fe, w, w0 et x. j' = jw j exp( jwt) ; j'' = -w2 j exp( jwt) ; repport dans j'' + 2 xw0j' +w02j = w02je. -w2 j exp( jwt) + 2 xw0 jw j exp( jwt) +w02j exp( jwt) = w02 Feexp( jwt). -w2 j + 2 xw0 jw j +w02j = w02 Fe. j = w02 Fe / [w02-w2+ 2j xw0 w]. Déterminer l'intervalle auquel appartient a. j = w02 Fe [w02-w2- 2j xw0 w] / [(w02-w2)2+ (2 xw0 w)2]. tan a = -2xw0 w / (w02-w2) ; si w tend vers zéro, alors tan a tend vers zéro ; a tend vers zéro par valeur négative. si w tend vers w0-, alors tan a tend vers -l'infini ; a tend vers -½p. si w tend vers w0+, alors tan a tend vers +l'infini ; a tend vers +½p. si w tend vers l'infini, alors tan a tend vers 2xw0 /w ; a tend vers zéro par valeur positive. a appartient à l'intervalle ]-½p ; +½p [. Ecrire j en excitation très basse fréquence. 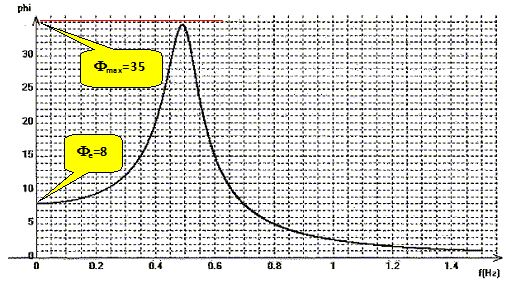j = w02 Fe / [w02-w2+ 2j xw0 w] avec w02>>w2 d'où j = w02 Fe / [w02+ 2j xw0 w] j = w0 Fe / [w0+ 2j x w] = w0 Fe [w0- 2j x w] / [w02+ 4 x2 w2] Module de j : |j | = F = w0 Fe / [w02+ 4 x2 w2]½ ; tan a = 2x w / w0. Ecrire j en excitation très haute fréquence. j = w02 Fe / [w02-w2+ 2j xw0 w] avec w02<<w2 d'où j = w02 Fe / [- w2+ 2j xw0 w] j = w02 Fe [- w2- 2j xw0 w] / [ w4+ (2 xw0 w)2] Module de j : |j | = F = w02 Fe / [w [ w2+ (2 xw0 )2] ½] ; tan a = 2x w0 / w. Tracer le diagramme asymptotique F(w) pour les TBF et les THF. TBF : F = Fe / [1+ 4 x2 (w/w0)2]½~ Fe(1-2 x2 (w/w0)2) ; asymptote F =Fe. THF : F = w02 Fe / [w2 [1+ (2 xw0/w )2] ½] ~ w02 Fe /w2 (1-2 x2 ( w0/w )2) ; asymptote F =0. Exprimer F en fonction de Fe, w, w0 et x. j = w02 Fe / [w02-w2+ 2j xw0 w] = w02 Fe [w02-w2- 2j xw0 w] / [(w02-w2)2+ (2 xw0 w)2] Module de j : |j | = F = w02 Fe/ [(w02-w2)2+ (2 xw0 w)2]½. Démontrer que F > Fe implique que w soit inférieur à une valeur à alculer en fonction uniquement de w0 et x. F >Fe ; w02 Fe/ [(w02-w2)2+ (2 xw0 w)2]½ > Fe ; w02 / [(w02-w2)2+ (2 xw0 w)2]½ > 1. w04 > (w02-w2)2+ (2 xw0 w)2 ; w04 >w04 + w4 - 2w02w2+ 4 x2w02 w2. 0 > w2 - 2w02+ 4 x2w02 ; w2 < 4w02(½-x2) ; w < 2w0(½-x2)½. Quelle condition sur x doit être vérifiée pour que la relation précédente soit possible ? ½-x2 >0 ; 0,5 >x2 ; x < 0,5½ ; x < 0,71. Dans le cas où x <<1, calculer la valeur maximale de F en fonction de Fe et x sachant que le maximum est lors en w~w0. F = w02 Fe/ [(w02-w2)2+ (2 xw0 w)2]½. Fmax ~w02 Fe/(2 xw02 ) ; Fmax ~ Fe/(2 x ). On a relevé F(f) avec f fréquence d'excitation. x =Fe/(2Fmax) =8/70 =0,114. Sachant que x =x0+ µI2 avec x0== 2,7 10-3 ; µ = 0,45 A-2 en déduire la valeur de l'intensité I. I = [(x -x0) /µ ]½ = [(0,114-2,7 10-3) /0,45 ]½ =0,25 A. Pour une intensité nulle dans les bobines, quelle valeur prendrait F à une fréquence d'excitation de 0,5 Hz ? Conclure. x =x0 = 2,7 10-3 ; 0,5 Hz est la fréquence de résonance, F = Fmax. Fmax ~ Fe/(2 x ) =Fe/(2* 2,7 10-3) = 185 Fe. L'amplitude à la résonance est trop grande : on va sans doute détruire une partie du système mécanique.

retour -menu