|
électronique : fonction de transfert, concours physique ITPE 2009. |
|||||||
|
|||||||
|
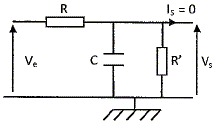
On note Y1 l'admittance complexe de la portion comprenant le condensateur et R' en dérivation : Y1 = 1/R' + jCw = (1+ jR'Cw) / R' ; impédance complexe Z1 =R' / (1+ jR'Cw). On note i l'intensité complexe qui travers R et Z1. Ve = (R+Z1 ) i ; Vs = Z1 i ; H = Z1 / (R+Z1 ) avec R+Z1=[ R (1+ jR'Cw) +R'] / (1+ jR'Cw) H =R' / (R+R'+ jR'RCw) = 1/(R/R'+1+jRCw). On note RCw = a ; H = 1/(R/R'+1+ja). Déterminer H pour R' infini. H =1/(1+ja). Déterminer H pour R' =R . H =1/(2+ja). Soit le montage ci-dessous dans lequel l'A.O est idéal.
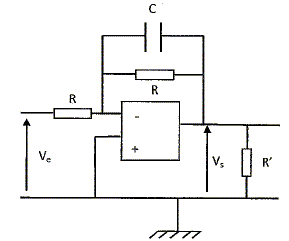
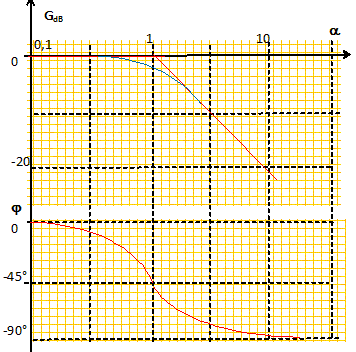
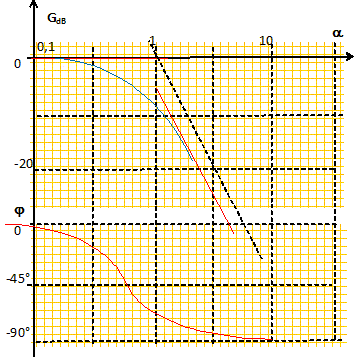
On note Z1 l'impédance complexe de la portion comprenant le condensateur et R en dérivation : Z1 =R / (1+ jRCw). L'entrée non inverseuse est reliée à la masse : l'entrée inverseuse est une masse virtuelle. Z1 et R sont traversée par la même intensité i. Vs = Z1 i ; Ve = -R i ; H = - Z1/ R H =-1/ (1+ jRCw). H = -1/(1+ja). Avantage de ce montage par rapport au précédent : la fonction de transfert est indépendante de la charge R'. Diagrammes de Bode : Module de H : |H|= (1-ja) / (1+a2) = (1+a2)-½. Gain en décibel : G = 20 log |H| = -10 log (1+a2) Si a2 est petit devant 1, G ~ -10 log 1 = 0 ; Si a2 est grand devant 1, G ~ -20 log a. tan j = -a ;
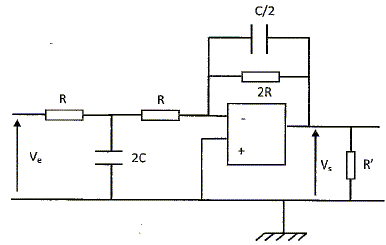
La fonction de transfert concernant la partie de droite ( A.O, R, 2R et ½C) a été déterminée ci-dessus ( second calcul). On remplace dans Z1 : ½C * 2R = CR, donc RCw = a ne change pas. Un calcul comparable conduit à : H1= -1/(1,5+ja). La fonction de transfert concernant la partie de gauche ( R, 2C) a été déterminée ci-dessus ( premier calcul avec R' infini). RCw = a devient 2RCw = 2a. H2= 1/(1+j2a). H =H1 H2= -1 / [(1,5+ja)(1+j2a)] H = -(1-2a2 -3,5ja) / [(1,5-2a2)2 +12,25a2] Diagrammes de Bode : Module de H : |H|= [(1,5-2a2)2 +12,25a2] -½. Gain en décibel : G = 20 log |H| = -10 log [(1,5-2a2)2 +9a2] Si a2 est petit devant 1, G ~ -10 log 1 = 0 ; Si a2 est grand devant 1, G ~ -10 log 4a4=-6 -40 log a. tan j = -3,5a /(1,5-2a2) ;
|
|||||||
|
|