Dispersion par un prisme concours physique ITPE 2009.

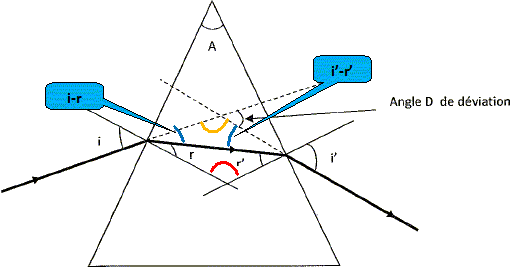
Pur un prisme d'indice n, placé dans l'air ( d'indice n=1) démontrer les deux formules donnant son angle au sommet A et la déviation D d'un rayon en fonction des paramètres indiqués sur le schéma. La somme des angles r+r' et l'angle A ont le même supplément ( l'angle noté en rouge) : A = r+r'. La somme des angles (i-r) et (i'-r') et l'angle D ont le même supplément ( l'angle noté en jaune) : D=i+i'-r-r' ; D = i+i'-A. On donne A = 48° et les indices du prisme pour deux radiations : n1 = 1,9 pour l1 = 768 nm ; n2 = 2 pour l2 = 470 nm. Ces deux longueurs d'onde sont aux extrémités du spectre visible. Quelles sont les couleurs des ces deux radiations ? l1 = 768 nm : rouge ; l2 = 470 nm : bleue. Un faisceau de lumière blanche arrive sur la face d'entrée du prisme. Le rayon de longueur d'onde l1 subit une réfraction à l'intérieur du prisme telle que la valeur de r soit r1 = 24 °. Que se passe t-il de particulier pour ce rayon ? Ce rayon est dévié vers la base du prisme. r' = 48-24 = 24 ° ; Appliquer la loi de Descartes pour la réfraction sur la seconde face du prisme : 1,9 sin 24 = sin i' sin i' = 0,772 ; i' = 50,6° ; ce rayon subit une nouvelle réfraction sur cette face. Quel est l'angle d'incidence du faisceau de lumière blanche ? sin i = 1,9 sin 24 = 0,773 ; i = 50,6 °. Calculer la déviation D1 du rayon de longueur d'onde l1. D1 = i + i'-A = 50,6 + 50,6 -48 = 53,2°.  Calculer la déviation D2 du rayon de longueur d'onde l2. sin 50,6 = 2 sin r2 ; sin r2 =0,386 ; r2 = 22,7 °; r'2 = A-r2 = 48-22,7 =25,3° réfraction sur la seconde face : 2 sin r'2 = sin i'2 ; sin i'2 = 2 sin 25,3 =0,854 ; i'2 =58,6 °. D2 = 50,6 + 58,6 -48 = 61,2°.  Conclure quand à la dispersion du prisme en fonction de la longueur d'onde. Le bleu, correspondant à la plus petite longueur d'onde, est plus dévié que le rouge, correspôndant à la plus grande longueur d'onde. Une couleur est d'autant plus déviée que sa longueur d'onde est plus petite. On choisit un prisme de même verre mais d'angle au sommet A'= 60°. Un rayon de longueur d'onde l2 l'attaque sous une incidence i = 30°. 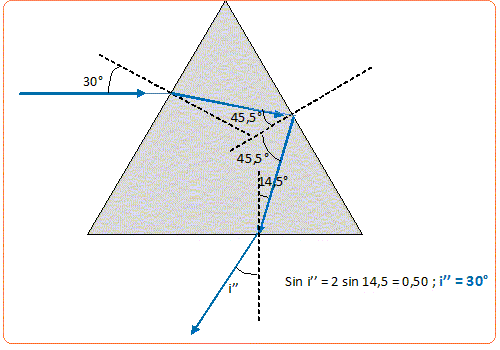Calculer les angles de ce rayon avec les normales aux faces du prisme rencontrées lors de son parcours et tracer son chemin à travers le prisme. Face d'entrée : sin 30 = 2 sin r ; sin r =0,25; r =14,5 ° ; r' = A-r = 60-14,5 =45,5 ° Deuxième face du prisme : 2 sin r' = sin i' ; sin i' = 2*sin 45,5 =1,43, valeur impossible Le rayon réfracté sur la seconde face n'existe pas : il y a réflexion totale sur cette face.

retour -menu