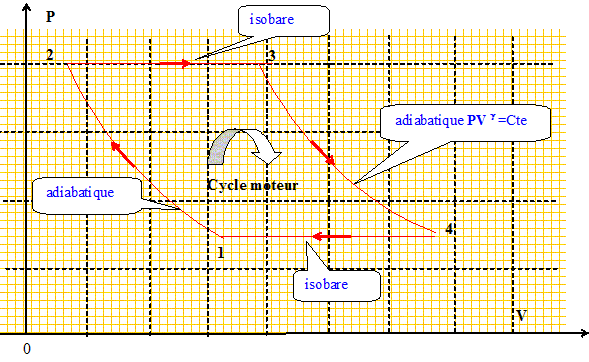
Turbine : cycle moteur : adiabatique, isobare concours physique ITPE 2009.

Le gaz décrivant le cycle sera supposé parfait. Le gaz initialement à la température T1 et sous la pression P1 est comprimé de manière adiabatique réversible jusqu' à l'état 2 ( température T2 et pression P2). Il se trouve alors au contact de la source chaude où il se réchauffe de manière isobare jusqu'à la température T3 ; il est alors dans l'état 3. Le gaz se détend ensuite de manière adiabatique réversible jusqu'à la pression P1. En fin de détente, sa température est T4, il est dans l'état 4. Il achève le cycle au contact de la source froide où il se refroidit de manière isobare pour se retrouver dans l'état 1. On note g = cp/cv, les capacités thermiques sont exprimées en J K-1 mol-1. Etablir pour un gaz parfait la relation : S2-S1 = cp ln ( T2/T1) -nR ln( P2/P1). dQ = ncvdT + PdV = ncpdT - VdP avec V = nRT/P ; dQ = ncpdT + nRT/P dP dS = dQ/T = ncp/TdT + nR/P dP , puis intégrer : S2-S1 = cp ln ( T2/T1) -nR ln( P2/P1) On rappelle la relation de Meyer cp-cv = nR. En déduire les expressions de cpet cv en fonction de n, R et g. g = cp/cv donne cp = cvg puis repport dans la relation de Meyer : cvg -cv = nR ; cv = nR /( g -1) ; cp= nRg /( g -1).   En déduire la realtion de Laplace en fonction de P et T. Lors d'une tranformation adiabtique réversible d'un gaz parfait PVg= cste Loi des gaz parfaits : PV = nRT ; V = nRT/P d'où : P ( T/P)g = cste soit P1-g Tg= cste. Tracer l'allure du cycle en indiquant le sens de parcours. Déterminer les expressions des températures T2 et T4 en fonction de P1, P2, T1, T3 et g. (1) à (2), transformation adiabtique réversible : P11-g T1g =P21-g T2g ; T2 = T1[P1 /P2 ](1-g) / g . (3) à (4), transformation adiabtique réversible : P31-g T3g =P41-g T4g ; Or P3 = P2 et P4 = P1 : les transformations 2-->3 et 4-->1 sont isobares ; par suite : T4 = T3[P2 /P1 ](1-g) / g . Etablir les expressions des travaux et des transferts thermiques en fonction des températures. 1-->2, diabatique réversible : Q12=0 ; la variation d'énergie d'un gaz parfait ne dépend que de la température : DU12 = ncvDT = W12. W12 = ncv(T2-T1). Même travail pour l'adiabatique réversible 3-->4 : Q34=0 ; W34 = ncv(T4-T3). 2-->3, isobare ; W23 = -P2DV = -P1(V3-V2) =P2V2 -P2V3 = P2V2 -P3V3 = nRT2-nRT3 ; W23 = nR (T2-T3). la variation d'enthalpie d'un gaz parfait ne dépend que de la température : DH23 = ncpDT = Q23. Q23 = ncp(T3-T2). Même travail pour l'isobare 4-->1 : W41 = nR (T4-T13) ; Q41 = ncp(T1-T4). Donner la définition du rendement h du cycle. h = -Wtotal / Qchaude. Travail récupéré divisé par l'énergie prélevée à la source chaude. Exprimer le rendement en fonction des transferts thermiques avec les sources chaude et froide. La variation d'énergie interne du gaz est nulle sur le cycle : DUcycle = 0 = W + Q. W = -Q avec Q23>0 ( reçu par la source chaude) et Q41<0 ( cédé à la source froide) W = Q41- Q23 ; h = (Q23+Q41 ) / Q23 ; h = 1+Q41 / Q23. Montrer que le rendement se met sous la forme : h = 1-a(1-g)/g avec a = P2/P1. Q41 / Q23 = (T1-T4) / (T3-T2) ; remplacer T2 et T3 par leur expression : T3-T2 =T4 [P1 /P2](1-g) / g-T1[P1 /P2 ](1-g) / g = (T4 -T1)[P1 /P2 ](1-g) / g. Q41 / Q23 = -1/[P1 /P2 ](1-g) / g = -[P2 /P1 ](1-g) / g ; h =1-[P2 /P1 ](1-g) / g . Avec lequel de ces trois gaz obtient-on le meilleur rendement ? gaz argon air CO2 valeur de g 1,67 1,40 1,31 (1-g) / g -0,41 -0,285 -0,237 a(1-g)/g ( a=4,0) 0,566 0,674 0,72 h 0,43 0,33 0,28 Donner la valeur de T2,T4 et h pour a = 4,0, g = 1,67, P1 = 1 bar, T1 = 300 K et T3 = 900 K. T2 = T1[P1 /P2 ](1-g) / g = 300 (0,25)-0,41=300*1,765 =530 K. T4 = T3[P2 /P1 ](1-g) / g = 900*4-0,41=900*0,566 =510 K. Dans le cas d'un cycle de Carnot évoluant entre une source froide à T1 et une source chaude à T3, le rendement maximun serait égal à : h = 1-Tfroide /Tchaude =1-T1/T3 =1-300/900 =0,67.

retour -menu