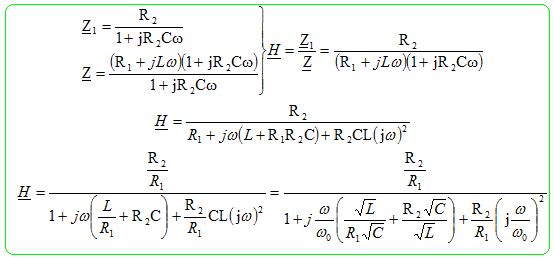circuits électriques, filtre, Bode , concours ITPE 2005

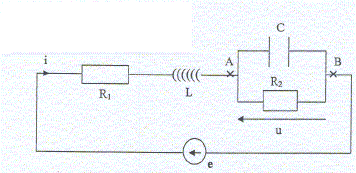
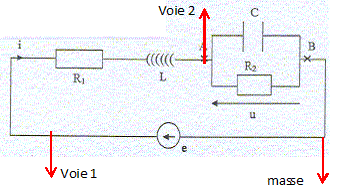
Le générateur e est une source idéale de tension qui délivre un signal e(t) dont la fonne est préciséeau fil des questions. On se propose d'étudier la tension u aux bornes du dipôle AB : «résistance R2 en parallèle avec la capacité C » R1 =R2 = 1 kW ; C= 1 nF ; L= 1mH. E= 1V; à t=0 u(0) =0 ; du(0)/dt = 0. Etude en régime transitoire. La tension e(t) est une tension créneaux de période T : si t appartient à [0, ½T]; e=E, régime forcé. Si t appartient à [½T ; T] ; e=0, régime libre. Préciser comment brancher un oscilloscope pour observer simultanément e(t) et u(t). voie 1, on observe e(t) ; voie 2 on visualise u(t). Ecrire l'équation différentielle vérifiée par u. On l'écrira sous la forme u" + 2l u' + w20 u = s. On note i1 l'intensité dans la branche contenant le condensateur et i2 l'intensité dans la branche contenant R2. Loi des noeuds : i = i1 +i2 avec i1 = Cdu/dt = C u' et i2 = u/R2 ; i = C u' +u/R2. Additivité des tensions : e = u + Ldi/dt + R1 i ; di/dt = Cu" + u'/R2. e = u + LC u" +L/R2 u' + R1C u' +R1/R2 u. e = (1+ R1 /R2 ) u + (L/R2 +R1C ) u' + LC u" u" + (1/(R2C) +R1/L ) u' + (1+ R1 /R2 ) /(LC) u = e/(LC). On pose : 2l = 1/(R2C) +R1/L = 1/(103*10-9) + 103 / 10-3 ; 2l = 2 106 s-1. w20 = (1+ R1 /R2 ) /(LC) = 2/ /(10-3*10-9) ; w20 =2 1012 ; w0 =1,4 106 rad s-1 et s = e/(LC) ; s = 1012 e. Résoudre cette équation différentielle : u" +2 106 u' + 2 1012 u = 1012 e (1) solution particulière ( régime permanent) : u = ½ e. Le condensateur chargé se comporte comme un interrupteur ouvert, la tension aux bornes de la bobine est nulle : e = (R1+R2)i avec u = R2 i = R2 / (R1+R2) e = ½ e. 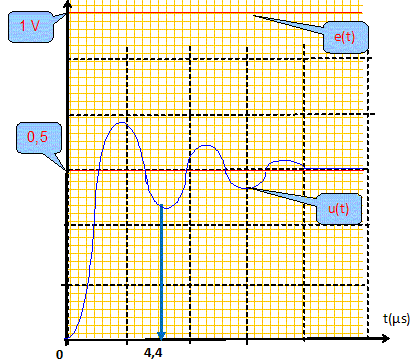Solution générale de : u" +2 106 u' + 2 1012 u =0 équation caractéristique : r2 + 2 106 r + 2 1012 =0 ; discriminant D = 4 1012 -8 1012 , valeur négative solution du type : u(t) = A exp(-lt) cos (w0t+j) Solution générale de (1) : u(t) = A exp(-lt) cos (w0t+j) +½ e. u(0 ) = A cos j +½ e = 0 ; u'(t) = -w0A sin j -l A cos j = 0 ; tan j = -l / w0 = -1/2½ ; j = -0,61 radian ; A = -0,5 e / cos j = -0,61 e. u(t) = e [ 0,5- 0,61 exp(-lt) cos (w0t-0,61) ]. u(t) = 1 [ 0,5- 0,61 exp(-106t) cos (1,4 106t-0,61) ]. Le régime est-il critique ? Pseudo-périodique ? Apériodique ? Justifier. Le régime transitoire est pseudopériodique ( discriminant D <0) : l'amplitude des oscillations diminue au cours du temps. Qu'appelle-t-on« régime transitoire» ? «Régime permanent» ? Que vaut ici la tension u en régime permanent ? En régime transitoire, le condensateur se charge, la bobine stocke de l'énergie. En régime permanent, la tension u est constante et sa valeur est égale à 0,5 e = 0,5 V. En supposant que la période T du signal créneaux est suffisamment grande pour observer le régime permanent, tracer sur un même graphe les deux tensions: e(t) et u(t). Le coefficient l est appelé «terme d'amortissement ». Comment influence-t-il le bilan énergétique ? Comment se comporterait le circuit si l était nul ? En cas d'amortissement, une partie de l'énergie est dissipée sous forme d'effet Joule. En absence d'amortissement ( R1 = 0; R2 infinie) : u"+w02 u = e(t) ; u" + 1012 u = 1012 e (1') ; solution particulière u(t) = e ; solution générale de u"+w02 u =0 : u = A cos (w0 t + j ) solution générale de (1') : u(t) = e + A cos (w0 t + j ) avec u(0) = 0 = e + A cosj. u'(0) = 0 = -Aw0sin j soit j = 0 d'où A = -e ; u(t) = e ( 1- cos (w0 t ). Etude du circuit en terme de filtre. 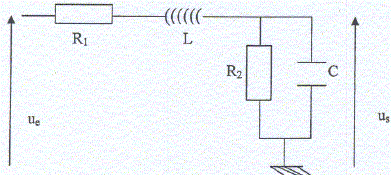La tension e(t) est à présent une tension sinusoïdale de la forme: e(t) = E cos(wt) ; E = 1 V Le circuit de la figure 1 est maintenant étudié en terme de quadripôle : la tension d'entrée est ue et la tensionde sortiee us = u. La fréquence, ou la pulsation w de la tension sinusoïdale e(t) peut varier. On étudie le filtre ainsi constitué décrit figure 2. Calculer la fonction de transfert H = Us / Ue du quadripôle. Les grandeurs soulignées sont des nombres complexes. On l'exprimera sous la forme H = H0 / ( 1+jx/Q +(jx)2) avec x = w /w0 et w0 = 1/(LC)½. On précisera les expressions de H0 et Q. Admittance complexe de R2 et C montés en dérivation : Y1 = 1/R2 + jCw = (1+jR2Cw ) / R2 Impédance complexe Z1 = R2 / (1+jR2Cw ). Impédance complexe de l'ensemble : Z = R1 +jLw + R2 / (1+jR2Cw ).    Définir et exprimer le gain en décibel du quadripôle. On appelle gain, la fonction , telle que GdB= 20 log H . Donner les équations des asymptotes de GdB aux basses fréquences et aux hautes fréquences. GdB= -10 log [(1-x2)2+Q-2x2 ] si x tend vers 0, alors GdB est équivalent à 0. L'axe des abscisses est asymptote horizontale. si x tend vers l'infini, alors GdB est équivalent à -40 log x. ( droite de pente -40 dB par décade). Cette droite asymptote coupe l'axe des abscisses en x=1. Exprimer GdB(w=w0). x=1 ; GdB(1) = -10 log Q-2 = 20 log Q. Tracer l’allure du diagramme de Bode en gain pour Q=10 et Q=0,1. On définit les pulsations de coupures wc d’un filtre par la relation : H <Hmax / 2½. Montrer que H passe par un maximum pour Q >2-½. 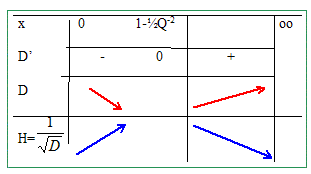On pose x = w2/w20 et on étudie la variation du carré du dénominateur. D= (1-x)2 + Q-2x= 1 +(Q-2-2)x + x2. chercher la valeur de x qui annule la dérivée D' : 2x +Q-2-2 =0 ; x = -½Q-2+1. x étant positif, alors Q-2<2 ou Q >2-½. 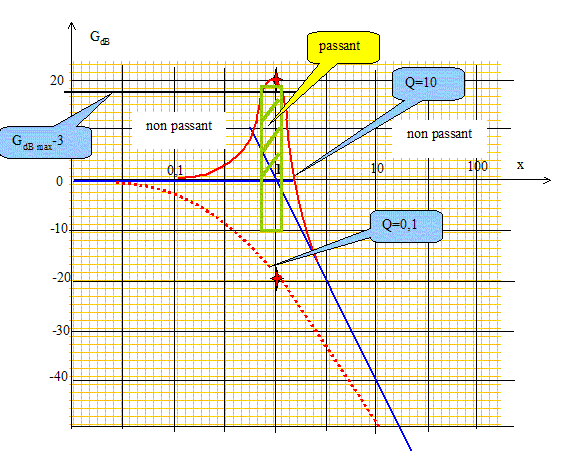Comment appelle-t-on ce phénomène ? résonance. De quel type de filtre s'agit-il ? Passe bande. Le filtre est d'autant plus sélectif que Q est grand.

retour -menu