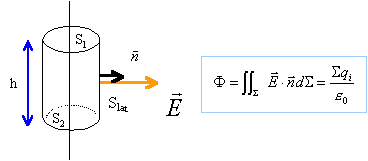|
champs électrique et magnétique crées par un cable coaxial , concours ITPE 2005 |
|||||||
|
|||||||
|
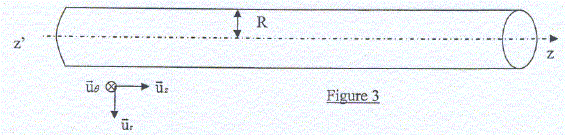
Les vecteurs sont écrits en gras et en rouge. On lui associe un système de coordonnées cylindriques de base (ur, uq, uz). Le cylindre porte des charges, qui selon le cas, sont immobiles ou en mouvement.
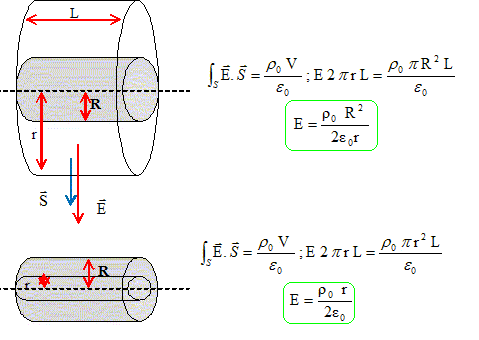
Etude d'une distribution volumique. Le cylindre porte la charge volumique r, fonction de la distance radiale r, telle que : si 0< r < R : r(r) = r0 ; si 0< r < R : r(r) = r0 ; si R < r : r(r) = 0. Les charges sont fixes. Rappeler le théorème de Gauss. L'appliquer pour calculer le champ électrique E en tout point de l'espace. La distribution de charge est invariante par translation suivant Oz : le champ ne dépend pas de la variable z. La distribution de charge est invariante par rotation autour de l'axe Oz : le champ ne dépend pas de l'angle q. Tout plan contenant l'axe du cylindre est plan de symétrie et tout plan perpendiculaire à l'axe du cylindre est également plan de symétrie (cylindre infini) donc le champ est radial. Le flux du champ électrique à travers une surface fermée (dite de Gauss, par exemple la surface d'uncylindre) est proportionnel à la charge contenue dans le volume délimité par la surface. Schéma fait pour r0 positive. Le flux du champ est nul à travers les sections du cylindre, celle-ci étant perpendiculaire au champ.
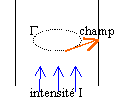
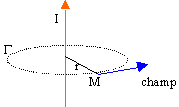
Les deux expressions donne pour r = R : E = r0R/(2e0). Le champ est continu en r=R. A la limite entre deux domaines, la composante normale du champ électrique présente une discontinuité égale à la densité surfacique de charges existant sur cette limite. Ici le cylindre est chargé en volume et ne porte pas de charge surfacique. Il n'y a donc pas discontinuité du champ électrique. Les charges sont à présent animées d'un mouvement rectiligne uniforme, caractérisé par la vitesse v, constante et uniforme, telle que : v = v0 uz. Ecrire le vecteur densité de courant, ou courant volumique, j (r) associé à ce mouvement de charges. Préciser son unité. Le vecteur densité de courant j (r) est défini par j (r) = r0 v avec r0 la densité volumique de charges mobiles et v la vitesse de l'électron libre. La densité volumique de charges mobiles peut s'écrire r0 = n e où n représente le nombre d'électrons libres par unité de volume. j (r) = r0v = n e v. ( unité A m-2) Rappeler le théorème d'Ampère. L'appliquer pour calculer le champ magnétique B en tout point de l'espace. Le champ B est-il continu en r = R ? La circulation C du champ magnétique le long d'une courbe fermée (G) quelconque est :
La densité de courant est j=I/(pR²), R rayon du conducteur. point intérieur au câble En tout point de G le champ magnétique a même module et est tangent à G. appliquer le th. d'Ampère sur le contour G, cercle de rayon r, l'intensité des courants enlacés par G étant I r²/R² B 2p r =m0 I r²/R² ; B =m0 I r / (2p R²) point extérieur au câble appliquer le th. d'Ampère sur le contour G, cercle de rayon r, l'intensité des courants enlacés par G étant I B 2p r =m0 I ; B =m0 I / (2p r) Si r =R on peut constater que le champ magnétique donner par les deux expressions ci dessus a la même valeur. Continuité du champ magnétique lors du passage du conducteur à l'air.
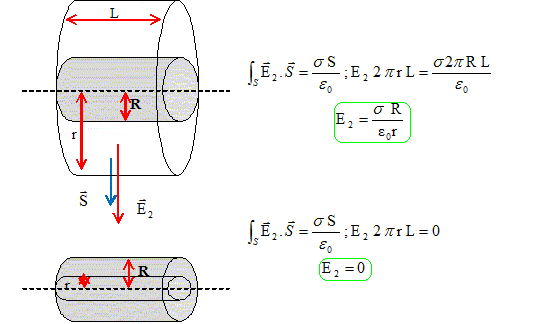
L'axe du cylindre est constitué d'un fil portant la charge linéique l. Le cylindre porte la charge surfacique s. Les charges n'existent qu'à la surface du cylindre, en r = R, et sur l'axe en r = O. Les charges sont fixes. Calculer les champs électriques en tout point de l'espace créé par la distribution linéique, E1, puis surfacique, E2. En déduire le champ total E. Champ électrique E1 crée par la distribution linéique :
On prend comme surface S un cylindre de hauteur h , d'axe la ligne infinie, et de rayon r. En tout point de la surface latérale le champ est radial et a même module, par raison de symétrie. Le fux du champ à travers la surface latérale est : F= E 2p r h Le flux du champ est nul à travers les bases S1 et S2, le champ étant perpendiculaire à la normale aux surfaces. D'autre part la charge contenue dans S est : Q = l h, l charge par unité de longueur. en appliquant le th de Gauss : E1 = l / (2p e0 r).
|
|||||||
|
|