Enthalpie ; sens d'évolution d'un système : synthèses HF et H2 concours ingénieur Minefe 2008.

Il est possible de synthètiser industriellement le fluorure d'hydrogène selon la réaction : (1) CaF2(s) + H2SO4(l) = CaSO4(s) + 2HF(g). On donne les enthalpies standards de formation DrH° et les entropies molaires standards Sm° à 25 °C : CaF2(s) H2SO4(l) CaSO4(s) HF(g) DfH° kJ mol-1 -1219,6 -814,0 -1434,1 -271,1 Sm° J mol-1 K-1 68,9 156,9 106,7 173,7   Définir et calculer la variance d'un système où se produit l'équilibre (1). La règle des phases donne la variance d'un système thermodynamique : v = c+2-j Le chiffre 2 indique le nombre de paramètres intensifs. c : nombre de constituants indépendants ( nombre de constituants - nombre de réactions chimiques indépendantes entre ces constituants) Nombre de constituants : c=4 ; nombre de relation : 1 ; nombre de phase : j= 4 v =  c-1+2-j= 4-1+2-4 =1. On peut faire varier la température ou la pression. Calculer l'enthalpie libre standard de cette réaction à 298 K ? Pour une mole de HF formé :(1) ½CaF2(s) + ½ H2SO4(l) = ½ CaSO4(s) + HF(g). DrH° =½DrH°(CaSO4(s)) + DrH°(HF) -½DrH°(H2SO4(l))-½DrH°(CaF2(s)) DrH° = -½*1434,1-271,1 +½ *814 + ½ *1219,6 ; DrH° = 28,65 kJ mol-1. DrS° =½S°(CaSO4(s)) + S°(HF) -½S°(H2SO4(l))-½S°(CaF2(s)) DrS° =½*106,7+173,7-½*156,9-½*68,9 = 114,15 J mol-1 K-1 DrG° =DrH° - TDrS° =28,65 - 298*0,11415 = -5,37 kJ mol-1 pour 1 mole de HF formé. Calculer la pression du fluorure d'hydrogène à l'équilibre à 25 °C. La constante d'équilibre s'écrit : K = PHF. De plus DrG° =-RT ln K ; ln K = -5,37 103/(-8,31*298) =2,17 K = 8,7 d'où PHF = 8,7 bar. A t-on intérêt à pratiquer cette synthèse à faible pression ou à haute pression ? Si la pression augmente, le nombre de molécules de HF croît : en conséquence l'équilibre est déplacé vers la gauche, sens indirect, diminution du nombre de molécules HF. On a donc intérêt à travailler à faible pression. En phase gazeuse, le fluorure d'hydrogène existe sous forme d'un polymère (HF)n qui se dissocie sous l'action d'une élévation de température en monomère HF. Expliquer le phénomène impliqué dans la polymérisation. Les molécules de fluorure d'hydrogène, même à l'état gazeux, peuvent être associées entre elles par des liaisons hydrogène forte. Synthèse du dihydrogène. Soit la synthèse suivante : CH4(g) + H2O(g) = CO(g) + 3H2(g). Cette réaction se fait sous pression totale constante Ptot = 10 bar. La température du réacteur est constante et à cette température, la constante d'équilibre thermodynamique K° est égale à 15. L'enthalpie standard de réaction est considérée comme indépendante de la température DrH° = 206 kJ / mol. Quelle est l'approximation faite sur la capacité calorifique de réaction à pression constante ? Quelle est la conséquence sur l'entropie molaire standard de réaction ? Sur l'enthalpie libre standard de réaction ?  DrCp varie très peu avec la pression si celle-ci est peu élevée ; DrCp est indépendant de la température si l'intervalle de température n'est pas trop grand. 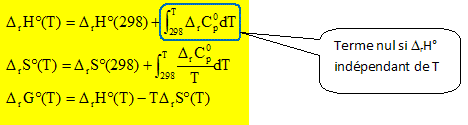DrH°(T) = DrH°(298) ; DrS°(T) = DrS°(298) ; DrG°(T) = DrH°(298)-TDrS°(298). Exprimer la constante d'équilibre K en fonction des pressions partielles et de la pression  standard P°=1 bar. K = PH23 PCO PCH4PH2O Les pressions partielles étant celles des constituants à l'équilibre. Initialement le système contient 10 moles de méthane, 30 moles d'eau, 5 moles de monoxyde de carbone et 15 moles de dihydrogène. Exprimer le quotient de réaction Qr en fonction des quantités de matière des constituants et de la pression totale Ptot. Calculer la valeur de Qr i dans l'état initial. avancement (mol) CH4(g) + H2O(g) = CO(g) + 3H2(g) initial 0 10 30 5 15 en cours x 10-x 30-x 5+x 15+3x A la date t, nombre total de mol : N= 60+2x. Fractions molaires : xH2 = 15+3x 60+2x ; xCO = 5+x 60+2x ; xCH4 = 10-x 60+2x ; xH2O = 30-x 60+2x Pressions partielles : PH2 =Ptot 15+3x 60+2x ; PCO =Ptot 5+x 60+2x ;PCH4 =Ptot 10-x 60+2x ; PH2O =Ptot 30-x 60+2x Quotient de réaction :   Qr= PH23 PCO PCH4PH2O = P2tot (15+3x)3(5+x) (10-x)(30-x)(60+2x)2 Valeur du quotient de réaction dans l'état initial : x=0 Qr i= = 102 153 *5 10*30*602 =1,56 Qr i est différent de K, le système n'est pas à l'équilibre. Qr i est inférieur à K, le système évolue spontanément dans le sens direct. Dans un nouvel état initial, le système ne contient que 10 moles de méthane et 10 moles d'eau. Déterminer la composition du système à l'équilibre. Ptot = 10 bar. Fractions molaires : xH2 = 3x 20+2x ; xCO = x 20+2x ; xCH4 = 10-x 20+2x ; xH2O = 10-x 20+2x Constante d'équilibre K= Qr éq= PH23 PCO PCH4PH2O = P2tot (3x)3(x) (10-x)(10-x)(20+2x)2 =100 27x4 4(10-x)2(10+x)2 15 *4 (100-x2)2 = 2700 x4 ; (100-x2)2 = 45 x4 ; 100-x2 = 6,71x2 ; x = 3,60 mol. Composition du système à l'équilibre : avancement (mol) CH4(g) + H2O(g) = CO(g) + 3H2(g) initial 0 10 10 0 0 à l'équilibre x éq=3,6 10-3,6 = 6,4 10-3,6 = 6,4 3,6 3*3,6 =10,8 Quelle est l'influence d'une élévation isobare de température sur cet état d'équilibre ? DrH° = 206 kJ / mol. : la réaction est endothermique. Une élévation isobare de température déplace l'équilibre dans le sens direct. Au système à l'équilibre on ajoute de façon isotherme et isobare, une mole de monoxyde de carbone. Dans quel sens se produira l'évolution ? Le système évolue dans le sens de la consommation de monoyde de carbone : sens indirect.

retour -menu