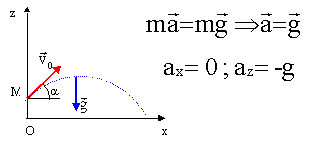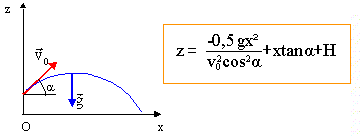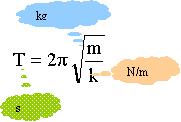Mécanique : projectile, oscillateur élastique horizontal concours technicien laboratoire éducation 2009.

On donne les masses volumiques de quelques métaux : ( en kg m-3 ) : aluminium : 2700 ; acier : 7850 ; nickel : 8900. On prendra comme valeur de l'intensité de la pesanteur : g = 9,81 m/s2. 1ère manipulation : mesures. Le diamètre de la bille est mesuré au pied à coulisse, on trouve 2,0 cm ; la bille est pesée sur une balance, on trouve 32,9 g. Est-elle fabriquée en aluminium, en acier ou en nickel ? Justifier. Volume : V = 4/3 *p*R3 = 4/3*3,14*0,013 =4,187 10-6 m3 ; masse m = 32,9 10-3 kg. masse volumique : m/V = 32,9 10-3 / 4,187 10-6 =7,8 103 kg m-3 ( acier). 2ème manipulation : mouvement dans un champ de pesanteur. La bille évolue dans le champ de pesanteur terrestre supposé uniforme. Le lanceur de la bille peut être incliné d'un angle a. La bille de masse m = 32,9 g est lancée d'un point M, repéré par son altitude OM= H. Le vecteur vitesse initiale fait un angle a avec l'horizontale. Si on néglige la résistance de l'air et la poussée d'Archimède, la bille n'est soumise qu'à son poids, force verticale, vers le bas, valeur mg. Dans un référentiel galiléen lié au sol, la seconde loi de Newton conduit à : Coordonnées du vecteur vitesse initiale v0 : v0x = v0 cos a ; v0z =v0 sin a. On appelle vx(t) la composante horizontale du vecteur vitesse et vz(t) sa composante verticale. Composantes horizontale et verticale vx(t) et vz(t) du vecteur vitesse du système au cours de son mouvement : Le vecteur vitesse est une primitive du vecteur accélération : vx(t) = v0 cos a ; vz(t) = -gt + v0 sin a. Nature du mouvement du projectile en projection sur l'axe horizontal : La valeur de la composante horizontale de la vitesse est constante : le mouvement est donc uniforme suivant Ox. Equations horaires du mouvement du projectile : x(t) et z(t). Le vecteur position est une primitive du vecteur vitesse : x(t) = v0 cos a t (1) z(t) = -½gt2 + v0 sin a t + H. (2) Equation de la trajectoire du projectile est la suivante : (1) donne t = x / v0 cos a. Repport dans (2). z = -½ g x2/ ( v0 cos a)2 + x tan a + H. Nature de la trajectoire du projectile : arc de parabole. A.N : a = 30° ; H=1,5 m ; la portée vaut : OP=3,50 m. Calculer v0. 0 = -0,5*9,81 *3,52/(v02 cos230) + 3,5 tan 30 +1,5 -80,115 /v02 + 3,52 = 0 ; v02 = 80,115 / 3,52 = 22,75 ; v0 =4,77 m/s ~ 4,8 m/s. 3ème manipulation : oscillations élastiques. 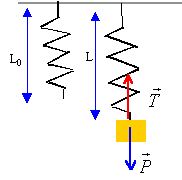La bille est accrochée à un ressort à spires non jointives de masse négligeable et de constante de raideur k. Equilibre du dispositif en position verticale : L'ensemble du dispositif ressort-bille est suspendu verticalement à un support fixe et placé dans le champ de pesanteur terrestre. Sur un axe vertical orienté vers le bas ( avec allongement x = L-L0) A l'équilibre tension et poids sont opposés: leurs normes sont égales : à l'équilibre le ressort s'est allongé de 4,1 cm. mg = k(L-L0) = k x , masse en kg et longueur en mètre k = 0,0329*9,81 / 0,041 =7,87 ~ 7,9 N/m. Mise en oscillations du dispositif en position horizontale. 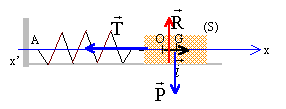La position du centre d'inertie de la bille est repérée par son abscisse x(t) sur un axe horizontal x'Ox. L'origine des abscisses correspond à l'abscisse de G lorsque la bille est à l'équilibre. Dans cette étude, tous les frottements sont négligés. Indiquer comment mesurer la période des oscillations à l'aide d'un chronomètre. Ecarté la bille de sa position d'équilibre vers la droite et lâcher le système sans vitesse initiale, tout en déclenchant le chronomètre. Mesurer par exemple la durée de 10 oscillations, puis diviser par 10 ; refaire 3 ou 4 fois la manipulation et faire la moyenne. Solution de l'équation différentielle et expression de la période.  poids et action du support se neutralisent. tension du ressort La seconde loi de Newton s'écrit, le référentiel terrestre étant supposé galiléen ; projection sur l'axe x'x : -k x = mx" ou x" + k/m x=0 ; pulsation w² = k/m   : Type de solution de l'équation différentielle : x= a sin(wt+j). période Déduction de la valeur de k à partir du graphique : k = 4p2 m/T2 = 4*3,142 *0,0329/0,42 =8,1 N/m. Ecart avec la valeur trouvée précédemment : (8,1-7,9) * 100 / 8 = 2,5 %. 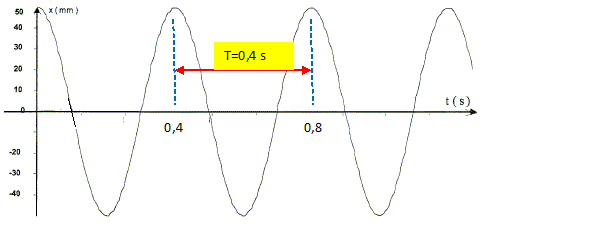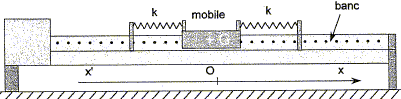Liste du matériel et schéma : Solide de masse m, posé sur un banc à coussin d'air horizontal et attaché à deux ressorts identiques de raideur k. Un capteur de position, non représenté, relié à un dispositif d'acquisition permet d'enregistrer la position du centre d'inertie G du mobile à chaque instant de date t. cette position est repérée sur un axe x'x horizontal, orienté de gauche à droite. L'origine O coïncide avec la position du centre d'inertie lorsque le mobile est à l'équilibre.

c

retour -menu