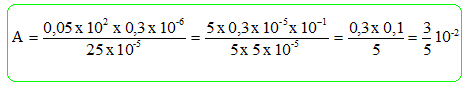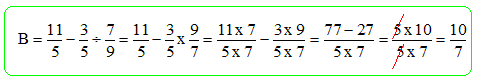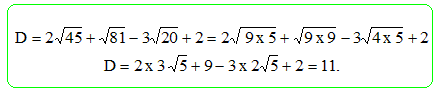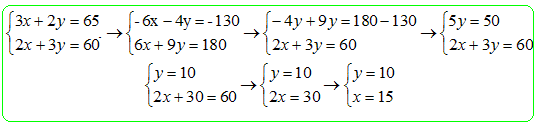Indiquer la bonne
réponse.
L'expression A est égale
à : 3 10-2 ; -3 10-2
; 3 / 5
10-2.
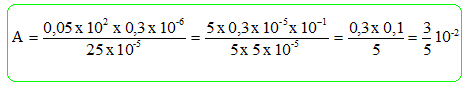
L'expression B est égale
à :10 / 7 ; -3 / 7 ; 1/ 7.
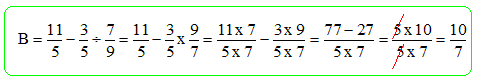
4 (x-3) - 3 (1 /3 -2x) = 13(x-1)
a pour
solution : -3 ; 0 ;
3
4x -12 -1 +6x = 13 x -13
10x -13 = 13x -13 ; 13 x -10x = 13-13 ; 3 x=0 ;
x =0.
|
|
L'expression C est
égale à : 16 ; 8 - 2
racine carre (5) ;
11.
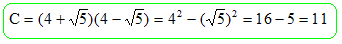
|
L'expression D est
égale à :
11 ; 5 - 5 ; 3 -2 ;
5
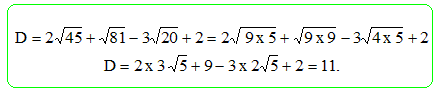
Résoudre le
système d'équations suivant par
combinaison :
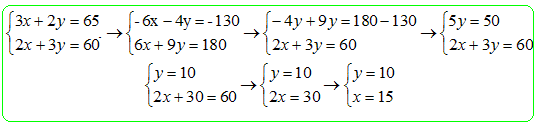
Un torréfacteur met en vente 2 sortes de
mélange de café. Le mélange A est
composé de 60 % d'Arabica et de 40 % de Robusta et
coûte 13 € le kilogramme.
Le mélange B est composé de 40 % d'Arabica
et de 60 % de Robusta et coûte 12 € le kilogramme.On
appellera X le prix du kilogramma d'Arabica et Y le prix du
kilogramme de Robusta.
Quel est le prix du kilogramme
d'Arabica et du kilogramme de Robustat ?
0,6 X + 0,4 Y = 13 (1) et 0,4 X +0,6 Y = 12 (2)
Multiplier tout par 5 afin de retrouver le système
ci-dessus.
3X +2Y = 65 et 2X +3Y = 60. (X = 15 et Y = 10 )
On donne l'expression suivante C =
(3x-2)2-25
Développer et
réduire
C.
C = 9x2-12x+4-25 ; C
=9x2-12x-21.
Factoriser
C.
Différence de deux
carrés A2-B2 = (A-B)(A+B) avec
A = 3x-2 et B =5.
C = (3x-2-5)(3x-2+5) =(3x-7)(3x+3)
=
3(3x-7)(x+1).
Calculer C pour X =
1/3.
(3x-2)2 =
(1-2)2 = 1 ; C =1-25 =
-24.
Résoudre (3x-7)(x+1)
=0.
3x-7 = 0 ; 3x = 7 ; x
=
7/3.
et x+1=0 ; x
=
-1.
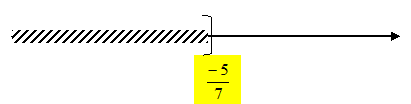
Résoudre l'inéquation
4x+7 >2-3x et représenter ses solutions sur une
droite graduée.
4x +3x >2-7 ; 7x >-5 ; x
>-5/7.
Le tableau ci-dessous indique la
répartition des élèves d'une classe
suivant leur taille.
Compléter le tableau
:
|
tranche de taille
|
taille en cm
|
effectif ni ( nombre
d'élèves)
|
fréquence fi en
%
|
effectifs cumulés croissants en
%
|
effectifs cumulés
décroissants en %
|
angles en °
|
|
A
|
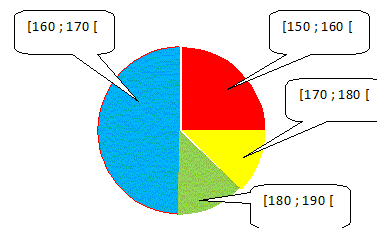
[150 ; 160 [
|
8
|
25
|
25
|
100
|
90
|
|
B
|
[160 ; 170 [
|
16
|
50
|
75
|
25
|
180
|
|
C
|
[170 ; 180 [
|
4
|
12,5
|
87,5
|
12,5
|
45
|
|
D
|
[180 ; 190 [
|
4
|
12,5
|
100
|
0
|
45
|
|
Total
|
xxxxxxxxxxxxx
|
|
100
|
xxxxxxxxxxxxxx
|
xxxxxxxxxxxxxx
|
360
|
Déterminer le nombre
d'élèves mesurant moins de 170
cm.
Taille inférieure à
170 cm ; 16 + 8 =
24.
Déterminer le nombre
d'élèves mesurant au moins de 170
cm.
Taille supérieure à
170 cm ; 4 +4 =
8.
Reproduire sur un diagramme
circulaire, les différentes tranches de tailles des
élèves.
|
|
Le prix officiel du véhicule Xsara
Picasso est de 20 000 € H.T. Sachant que le taux de
TVA appliqué est de 19,6 %,
quel est le prix d'un
tel véhicule TTC ?
20 000 *1,196 = 23 920
€.
On a relevé les notes obtenues par de
élèves à un devoir de
mathématiques.
|
notes
|
7
|
8
|
8,5
|
9
|
10
|
11
|
13
|
15,5
|
18
|
|
effectifs
|
1
|
2
|
2
|
4
|
4
|
6
|
2
|
2
|
2
|
Calculer la moyenne en
détaillant les calculs.
Effectif total : 1 +2 +2 +4 +4 +6 +2 +2 +2 =
25.
moyenne : (7 +8*2 +8,5*2 +9*4 +10*4 +11*6 +13*2
+15.5*2 +18*2) / 25
(7 +16 +17 +36 +40 +66 +26 +31 +36) / 25 =
11.
Déterminer la
médiane en justifiant.
La médiane
est le nombre qui permet de couper la
population étudiée en deux groupes
contenant le même nombre d'individus
L'un des groupe a des notes supérieures
à la note médiane, l'autre groupe a
des notes inférieures à la note
médiane.
notes
|
7
|
8
|
8,5
|
9
|
10
|
11
|
13
|
15,5
|
18
|
effectifs
|
1
|
2
|
2
|
4
|
4
|
6
|
2
|
2
|
2
|
effectif cumulé croissant
|
1
|
3
|
5
|
9
|
13
|
19
|
21
|
23
|
25
|
(25 +1) / 2 = 13 ; la note médiane est la 13è note, c'est à dire 10.
Mika propose des boules de glace de 2 cm de
rayon.
Calculer le volume
d'une boule en fonction de pi.
4 /3 pi R3 = 4/3 pi *23
=10,67 pi
cm3.
Des clients très gourmands ont
réclamé des boules plus grosses. Mika
a doublé le rayon de ces boules.
Par combien le volume
d'une boule a t-il été
multiplié ?
Le volume est proportionnel au cube du rayon ;
si le rayon double, le volume est multiplié
par
23=8.
|