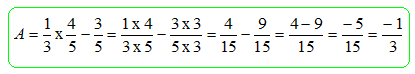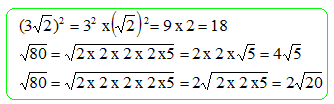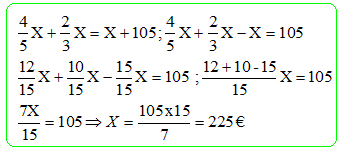Mathématiques : concours ASPTS agent spécialiste police technique et scientifique ; Sud-Ouest 2007.

Indiquer la ou les bonne réponses. La valeur de l'expression A est égale à : 1/15 ; -5/15 ; -13/15 ; -1/3. La multiplication est prioritaire sur l'addition et sur la soustraction. Dans une assemblée, les 3/4 des participants sont des femmes, les deux tiers des hommes portent des lunettes et l'on compte 10 hommes qui portent des lunettes. Quel est le nombre total de participants à cette assemblée : Sur 100 participants il y a 25 hommes ; sur 300 participants, il y a 75 hommes ; sur 75 hommes il y en a 75*2/3 = 50 qui portent des lunettes. Pour 10 hommes avec lunettes il y a donc 300 *10 / 50 = 60 participants. Autre méthode : on note N le nombre de participants ; 0,25 *2/3 N = 10 ; n = 10*3 /(0,25*2) =60. Lorsqu'on double le rayon d'un cerle, son aire est multipliée par : 2 ; 4 ; 6 ; 8. Aire d'un disque p r2 ; l'aire étant proportionnelle au carré du rayon, si le rayon double, alors l'aire est multipliée par 4. Lorsque l'on double les trois dimensions d'un parallélépipède, son volume est multiplié par : 2, 4, 6, 8. Volume = largeur * longueur * hauteur. Chaque dimension étant doublée, le volume est multiplié par 8. Soit un triangle ABC tel que AB = 1 cm. On place les points B' et C' tels que B' appartienne à [AB) et BB' = 2 cm, C' appartienne à [AC) et AC' = 7,5 cm ; (BC) et (B'C') sont parallèles. 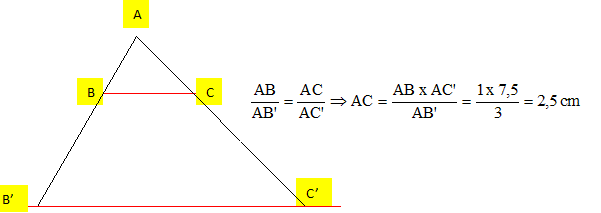Le théorème qui permet de calculer la longueur AC est : - le théorème de pythagore, - le théorème de Thalès, la relation de Chasles, autre théorème.   La longueur AC est alors égale à : 2,3 cm ; 2,4 cm ; 2,5 cm ; 2,7 cm. Une horloge sonne six heures du matin en six secondes. En combien de temps sonne telle midi ? 12 s ; 12,2 s ; 13 s ; 13,2 s. six heures : six coups de marteau sur la cloche ( émission des sons) et six temps morts durant lesquels le son se propage puis s'atténue. Pour 12 heures : 12 s. En informatique, on code des nombres de 8 chiffres en utilisant uniquement les chiffres 0 et 1. Combien de nombres peut-on coder : 27 ; 256 ; 128 ; 28. Classer par ordre décroissant les séries suivantes : 5,04 102 ; 540 100 ; 0,5004 103 ; 54,04 101. 504 ; 540 ; 500,4 ; 540,1 d'où : 540,1 ; 540 ; 504 ; 500,4. 28 /9 ; 3,1 ; 10/3 ; 14/5 ; 17/5. 3,111 ; 3,1 ; 3,33 ; 2,8 ; 3,4 d'où : 17/5 ; 10/3 ; 28 /9 ; 3,1 ; 14/5. Le 21 août 1989 la sonde Voyager II arrive à proximité de la planète Neptune. Cette planète se trouve à 4,5 milliards de km de la Terre. Les signaux émis par la sonde arivent sur la Terre à la vitesse de 300 000 km /s. Combien de temps ont-ils mis, en heures, minutes et secondes pour parvenir à la Terre ? 4,5 milliards de km = 4,5 109 km : 300 000 km/ s = 3 105 km/s. durée (s) =distance (km ) / vitesse (km/s) = 4,5 109 / 3 105 = 1,5 104 s 15 000 / 3600 = 4 heures et 600 s = 4 heures 10 minutes.   L'équation (2x-3)(4x+2) =0 admet pour solutions : 2/3 ; 3/2 ; 2/4 : -1/2. 2x-3 =0 d'où x = 3/2. et 4x+2 =0 d'où 4x =2 ; x = -2/4 ; x = -1/2. A la oulangerie un client demande : " 4 baguettes et 5 croissants". Il paie 8,10 €. Une autre cliente demande ;" 2 baguettes et 3 croisants". Il paie 4,60 €.  Quel est le prix d'une baguette ? celui d'un croissant ? On note X le prix d'une baguette et Y celui d'un croissant. 4X + 5 Y = 8,1 (1) et 2X + 3Y = 4,6 (2). multiplier (2) par 2 : 4X + 6Y = 9,2 puis soustraire, d'où : 6Y-5Y = 9,2 -8,1 ; Y = 1,1 €. Par suite (1) donne : 4X + 5,5 = 8,1 ; 4X = 8,1-5,5 ; 4X = 2,6 ; X = 2,6 / 4 ; X = 0,65 €. Un client achète dans un supermarché 5 bouteilles de jus d'orange et 3 bouteilles de pomme pour 16,4 euros. Le jour suivant il rachète 3 bouteilles de jus d'orange et 5 bouteilles de jus de pomme pour 15,6 euros. Le prix d'un litre de gasoil était de 1,120 €. Il augmente un jour de 10 % puis diminue le jour suivant de 10 %. Le prix subit alors une variation de : -1 % ; 0,0112 € ; 0 € ; -0,0112 € ; 1 %. Prix après augmentation : 1,120 *1,1 =1,232 € Prix après diminution : 1,232*0,9 = 1,1088 € Différence : 1,1088-1,120 = -0,0112 €. soit en pourcentage : -0,0112*100 / 1,12 = -1 %. On a compter les véhicules franchissant un péage d'autoroute pendant une heure. Les vhicules sont classés dans les catégories suivantes : voitures, camions, autocars, motos. On a noté que 112 autocars ont franchi le péage ce qui représente 16 % de la totalité des véhicules et on a compté 84 motos et 168 camions. Calculer le nombre total de véhicules ayant franchi le péage en une heure. 112 / 16 = 7 ; pourcentage de motos : 84/7 = 12 % ; pourcentage de camions : 168 / 7 = 24 % pourcentage de voitures : 100 -16 -12 -24 = 48 % ; nombre de voitures : 48*7 =336 Total véhicules : 112 + 84 + 168 + 336 = 700 véhicules. Ou bien : 112/16 = 7 ; 1 %correspond à 7 véhicules ; par suite 100 % correspond à 700 véhicules. Compléter le tableau suivant : catégories autocars motos camions voitures total nombre de passages 112 84 168 336 700 fréquences ( %) 16 12 24 48 100   On a relevé le temps de passage de chacun des 168 camions. On a noté que 60 camions ont mis 45 s pour passer, 68 ont mis 50 s et 40 ont mis 55 s. Calculer le temps moyen de passage d'un camion (à 0,1 s près ). (60 *45 + 68*50 + 40 *55 ) / 168 = (2700 +3400 + 2200 ) / 168 =49,4 s. 5 x 10-3 sécrit : 50-3 ; 0,05 ; 0,005 ; -150. 5 x 10-3 = 5 / 103 = 5 /1000 = 0,005. 275 s'écrit en notation scientifique : 2,75 102 ; 2,75 10-2 ; 0,275 103 ; 275. Deux frères veulent acheter un lecteur de disques vidéos. L'un deux possède les 4/5 du prix de ce lecteur tandis que l'autre possède les 2/3. Ils mettent leurs économie en commun pour acheter ce lecteur. Il leurs reste alors 105 €. Quel est le prix de l'appareil ? On note X le prix de l'appareil : 4/5 X + 2/3 X = X +105. Un automobiliste roule sur l'autoroute à une vitesse moyenne de 120 km/h pendant une durée de 3 h 39 min. Sachant qu'il consomme 6,3 litres d'esence pour 100 km, calculer sa consommation sur le parcours à 0,1 L près. 3 h 39 min = 3*60 +39 = 219 min ; 120 km/h = 120 / 60 m/min =2 km /min. Distance parcourue : 219*2= 438 km. Puis 438 / 100 * 6,3 = 27,6 L. Une entreprise de menuiserie fabrique 150 chaises par jour ; elle produit deux sortes de chaises, les unes vendues 38 € pièce, les autres 61 € pièce. L'entreprise souhaite que le montant des ventes soit strictement supérieur à 7386 € par jour et elle veut fabriquer plus de chaises à 38 € que de chaises à 61 €. Elle doit fabriquer un nombre de chaises à 38 € égal à : 74; 75 ; 76 ; 77. On note X le nombre de chaises à 38 €. 38 X + 61 (150-X) >7386 et X >150-X ; 2X > 75 ; X > 75. 38 X -61 X +150*61 > 7386 -23 X +9150 >7386 ; 9150 -7386 > 23 X ; 1764 >23 X 1764 / 23 >X ; 76,7 > X X doit être supérieur à 75 et inférieur à 76,7 ; X est entier et vaut donc 76. On augmente la longueur d'un rectangle de 10 % et on diminue sa largeur de 10 %. L'aire du rectangle à t-elle varier ? Justifier. Aire initiale = longueur fois largeur Nouvelle aire = 1,1 longueur fois 0,9 largeur = 1,1 x 0,9 fois aire initiale = 0,99 aire initiale L'aire initiale diminue donc de 1 %.

retour -menu