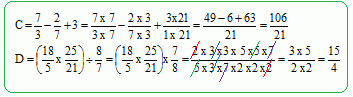|
Calculer les expressions en détaillant : A = -7 -3 x9 + 8 = -7 -27 +8 = -34+8 = -26.
B = -4(6-11)+1 = -4 (-5)+1 = 20+1=21.
Exprimer ces deux expressions sous forme d'une fraction simplifiée en détaillant.
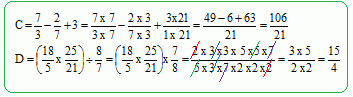
Exprimer ces deux fonctions sous forme d'un nombre décimal en détaillant les calculs.
E = 9 x 105 x 3 x (103)-2 / (12 x 10-4) = 9 x 105 x 3 x 10-6 x 104 / 12
E = 27 x 105-6+4 / 12= 9 x 103 / 4 =2250.
F = 5,2 103 - 0,07 x 102 + 5 x 4 x 10-1 =5200-7 + 2 = 5195.
|
|
L'expression algébrique suivante est égale à :
G = (3x+8)(3x-8) - (4x+7)2.
G = 9x2 -64 -(4x+7)2.
G = 9x2 -64 -(16x2+56x+49)
G = 9x2 -64 -16x2-56x-49.
G = -7x2 -56x -113.
|
Un champ rectangulaire a les dimensions indiquées en fonction de x.
Largeur BC = 3 x + 7 ; longueur AB = 5x-2.
Calculer l'aire de ce champ en hectare si x = 4 dam.
x = 4 dam = 40 m ; BC = 3*40+7 = 127 m ; AB = 5*40-2 = 198 m
Aire : BC x AB = 127 * 198 = 25 146 m2
1 ha = 10 000 m2 ; l'aire vaut 2,51 ha.
Sachant que l'agriculteur qui cultive ce champ doit laisser 10 % de la surface en jachère,
calculer l'aire de la surface cultivable de ce champ en ha.
90 % sont cultivés soit : 0,9*2,51 = 2,26 ha.
Paul a obtenu quatre notes en mathématiques, 14 / 20, 10 / 20, 12 / 20 et 7 / 10.
Quelle est sa moyenne sur 20 arrondie au centième ?
7 / 10 possède le coefficient 0,5, les autres notes le coefficient 1 : puis : (14 + 10 +12 +7) / 3,5 =12,29 / 20.
Résoudre les équations suivantes en donnant les valeurs exactes des résultats :
-9x + 5 = 2(x-6).
-9x + 5 = 2x -12 ; 5 + 12 = 2x + 9x ; 17 = 11 x ; x = 17 / 11.
(8x-6) ( 5x+2) = 0.
.8x-6 = 0 ; 8x = 6 ; 4x = 3 ; x = 3/4.
5x + 2 = 0 ; 5x = -2 ; x = -2 / 5.
On donne les deux équations suivantes : x + y = 5 ; 2x - y = 1.
Représenter
sur le même graphique, l'ensemble des solutions de ces deux
équations puis en déduire par siple lecture la solution du
système constitué par ces deux équations.
x + y = 5 s'écrit y = 5-x, c'est l'équation d'une droite passant par les points : A ( x=0 et y= 5); B( x=5 et y=0)
2x - y = 1 s'écrit y = 2x-1, c'est l'équation d'une droite passant par les points : C ( x=0 et y= -1); D( x=2 et y=3)
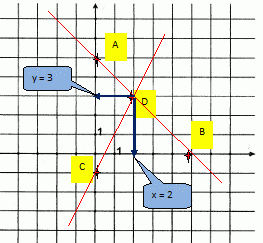
Vérifier le résultat par le calcul.
y = 5-x et y = 2x-1 donne : 5-x = 2x-1 ; 5+1 = 2x + x ; 6 = 3x ; x=2.
par suite y = 5-2 = 3.
|
|
Une voiture consomme en moyenne 8,6 L pour 100 km.
Combien consommera t-elle pour parcourir 367 km ? Justifier.
La voiture consomme 8,6 / 100 = 0,086 L par km
Puis : 0,086*367 = 31,56 L ~ 32 L.
Quelle distance pourra t-elle parcourir avec 39,4 L ? ( arrondir le résultat au mètre près)
39,4 / 0,086 = 458,140 km.
Compléter en cochant les bonnes cases.
Si une série a une moyenne de 3,5, alors on sait obligatoirement :
- il y a des valeurs inférieures ou égales à 3,5 et des valeurs supérieures ou égales à 3,5. ( vrai)
- il y a autant de valeurs inférieures oun égales
à 3,5 que de valeurs supérieures ou égales à 3,5. (faux, cela
correspond à la définition de la médiane )
- la valeur la plus fréquente est 3,5.
On donne la série statistique ordonnée suivante :
Déterminer la valeur de b sachant que la médiane est égale à 9.
valeur
|
6
|
8
|
9
|
10
|
11
|
a
|
effectif
|
3
|
4
|
1
|
2
|
3
|
b
|
La médiane est le nombre qui permet
de couper la population étudiée en deux groupes contenant le même nombre
d'individus.
A gauche de la valeur 9, l'effectif total est égal à 3+4=7.
A droite de la valeur 9, l'effectif total doit être égal à 7 d'où : 2+3+b = 7 ; b = 2.
Déterminer a si la moyenne de cette série est 10.
Effectif total : 3 + 4+1+2+3+2 = 15
(6*3 + 8*4 +9*1 +10*2 +11*3 +2a) / 15 = 10
112 + 2a = 150 ; 2a = 150-112 = 38 ; a = 19.
Quelle est l'étendue de cette série statistique ?
L'étendue d'une série est la différence entre la plus grande et la plus petite valeur du caractère :
19-6 = 13.
Construire le diagramme en bâtons de cette série.
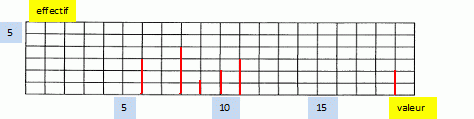
|
|