Le flash électronique concours Mines 2009.

Le fonctionnement d’un flash électronique repose sur la génération d’un éclair dans un tube à décharge. Il s’agit d’un tube de quartz dans lequel on a placé un gaz raréfié, le xénon, entre deux électrodes E1 et E2. Ces deux électrodes sont reliées à un condensateur de capacité C chargé sous quelques centaines de volts. Autour du tube est enroulé un fil constituant une électrode E3. On peut appliquer entre E1 et E3 une impulsion de tension de plusieurs milliers de volts qui ionise le xénon. Il devient alors conducteur et le condensateur peut se décharger dans le gaz, créant ainsi un éclair lumineux très intense d’une durée très brève. Le fonctionnement du flash est étudié dans trois parties indépendantes.  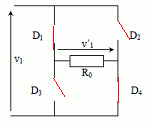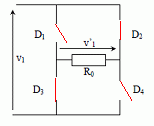Partie B1 : Etude du redresseur. Le condensateur doit être chargé sous une tension continue v2 de l’ordre de 0,30 kV. Le flash étudié n’est cependant alimenté que par des piles fournissant une tension continue de 6,0 V. Afin d’obtenir la tension v2 nécessaire, la tension d’alimentation est dans un premier temps convertie en une tension alternative pour être ensuite élevée dans un transformateur. On obtient en sortie du transformateur une tension alternative v1 qu’il faut redresser et filtrer pour obtenir la tension continue v2. Le pont de diodes constituant le redresseur est représenté. Il est composé de quatre diodes D1, D2, D3 et D4. 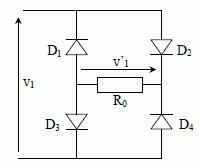Tracer sur le graphe figurant en annexe l’allure de la caractéristique d’une diode à jonction dans le modèle de la diode idéale sans seuil. Préciser à quel composant est équivalente la diode dans chacune des zones de la caractéristique. 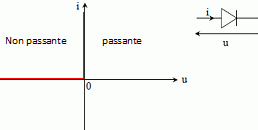La diode passante est équivalente  à un interrupteur fermé ; la diode non passante est équivalente  à un interrupteur ouvert. Qu’est ce qui justifie ici l’application du modèle de la diode idéale sans seuil ? La tension v1 est de l'ordre de la centaine de volt ; la tension de seuil d'une diode est  de l'ordre du volt. La tension v1(t) obtenue en sortie du transformateur est une tension sinusoïdale de pulsation ω et de période T : v1(t) =V1 sin(wt) Dessiner le circuit équivalent au montage lors d’une alternance positive de la tension v1(t). En déduire l’expression de la tension v’1(t) sur cette alternance. v'1(t) =V1 sin(wt) avec t compris entre 0 et ½T.  Reprendre les mêmes questions lors d’une alternance négative de la tension v1(t). v'1(t) =-V1 sin(wt) avec t compris entre ½T et T. 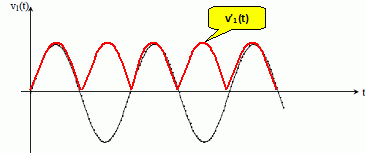Tracer sur le graphe figurant en annexe l’allure de la tension v’1(t) en sortie du redresseur. Partie B2 : Génération de l’éclair.  Le gaz du tube à décharge n’est a priori pas conducteur. Cependant, lorsqu’une très haute tension est appliquée entre deux de ses électrodes, l’ionisation des atomes de xénon qui en résulte abaisse la résistance du tube qui devient alors équivalent à un conducteur de résistance RT dans lequel le condensateur C peut se décharger.  Expliquer pourquoi l’ionisation des atomes de xénon abaisse la résistance du tube à décharge. L'ionisation des atomes donne des ions positifs et des électrons. Les électrons libérés sont attirés vers l'électrode positive et les ions  positifs par l'électrode négative. Un énorme flux d'électrons traverse le tube : à un grand nombre de porteurs de charges mobiles correspond une résistance électrique faible. 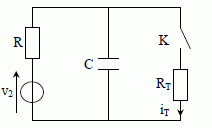On utilise le circuit équivalent de la figure ci-dessous pour expliquer la formation d’un éclair dans le tube. On considère que la tension v2, obtenue par filtrage de v’1 est une tension continue de 0,30 kV. Le régime permanent étant atteint pour t < 0, on ferme l’interrupteur K à l’instant t = 0. Déterminer les expressions iT(0+) et iT(∞) de iT juste après la fermeture de l’interrupteur et lorsque le régime permanent est atteint (après la fermeture de l’interrupteur). Avant la fermeture de l'interrupteur, le condensateur est chargé  : la tension  à ses bornes est v2. Le xénon étant devenu conducteur  le condensateur peut se décharger très rapidement dans le gaz :  iT(0+) = v2 / RT. Ensuite la résistance  RT du tube revient  à une valeur très élevée : le condensateur se recharge. Le condensateur chargé se comporte comme un interrupteur ouvert en courant continu. par suite v2 = (R+RT) iT(∞) ; iT(∞) = v2 / (R+RT). RT étant très élevée, iT(∞) est proche de zéro. Déterminer l’équation différentielle vérifiée par iT(t) pour t > 0. On pourra y faire apparaître la constante de temps t = RRTC / (R+RT). 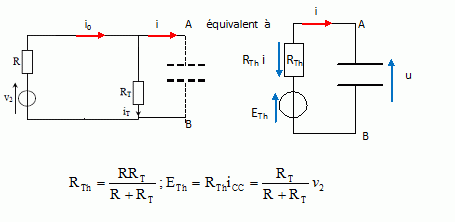On recherche l'expression de i(t) : Additivité des tensions : u = ETh-RTh i ; avec u = q/C et i = dq/dt  ; d'où q/C+RTh dq/dt = ETh ; dq/dt + q/(CRTh ) = ETh / RTh. On dérive par rapport au temps et on remplace dq/dt par i et d2q/dt2 par di/dt : di/dt + i /(CRTh) =0 ; di/dt + i / t =0 ; Ecrire la loi des noeuds : i0 = i + iT. Exprimer de deux manières différentes la tension aux bornes du condensateur : RT iT = v2-Ri0. i0= v2 / R- RT / R iT = i + iT. Dériver par rapport au temps : ( v2 est constant) - RT / R diT /dt =  di /dt + diT /dt. -(1+RT / R )diT /dt =  di /dt.  et i = v2 / R-(1+ RT / R )iT. di/dt + i / t =0 s'écrit :  -(1+RT / R )diT /dt -(1+ RT / R )/ t iT + v2 / (Rt)=0 diT /dt + iT / t = v2 / (RRTC).   Web www.chimix.com En déduire l’expression complète de iT(t) pour t > 0 en fonction de v2, R, RT, t et τ. diT /dt + iT / t = v2 / (RRTC). Solution générale de l'équation sans second membre : iT(t) = A exp(-t/ t). Solution particulière de l'équation différentielle avec second membre : iT(∞) = v2 / (R+RT). Solution générale de l'équation avec second membre : iT(t) = A exp(-t/ t)+ v2 / (R+RT). A est déterminé par la condition initiale : iT(0+) = v2 / RT. v2 / RT =A +v2 / (R+RT) ; A = v2R / [RT(R+RT)] iT(t) = v2  R / [RT(R+RT)] exp(-t/ t)+ v2 / (R+RT). iT(t) = v2 / (R+RT) [ R / RT exp(-t/ t)+1 ]. Tracer l’allure de iT(t) pour t < 0 et t > 0 et expliquer la génération d’un éclair lors de la fermeture de l’interrupteur K. à t <0, l'interrupteur K est ouvert : iT(t) =0 à t =0+,  iT(t) présente un pic d'intensité, ce qui génère un éclair. 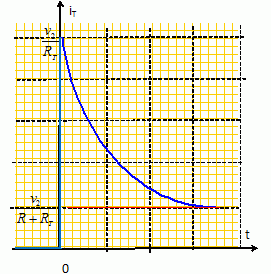Partie B3 : Etude énergétique. On raisonne toujours dans cette partie à l’aide du schéma électrique simplifié de la figure ci-dessus. Donner l’expression de l’énergie accumulée par le condensateur avant la fermeture de l’interrupteur. E= ½C v22. On souhaite générer un flash d’une puissance égale à 4,0 W et d’une durée de 0,10 s.  Calculer l’énergie moyenne devant être stockée dans le condensateur. Energie moyenne = puissance * durée Emoy = 4,0*0,10 = 0,40 J. Déterminer un ordre de grandeur de la valeur de la capacité C nécessaire. Commenter ce résultat. v2 est de l’ordre de 0,30 kV. C = 2Emoy /v22=0,80 / 3002=8,9 10-6 F ~10 µF. Cette valeur est assez faible pour une capacité. Néanmoins ce condensateur peut stocker suffisamment d'énergie pour alimenter le flash, l'énergie étant libérée en une durée très courte.

retour -menu