Chimie : chlore, dichlore, chlorure, précipitation, conductimétrie concours Mines 2009.

Constante des gaz parfaits R = 8,314 J.K-1.mol-1. T0 = 273 K correspond à 0°C.  Le chlore a pour numéro atomique Z = 17. Masse atomique molaire de H : 1 g.mol-1 Masse atomique molaire de Cl : 35,5 g.mol-1 (g), (l), (s), (aq) après la formule d’une espèce chimique signifient respectivement gazeux, liquide, solide et aqueux. Généralités.  Que représente le numéro atomique d’un élément chimique ? Le numéro atomique représente le nombre de protons du noyau de l'atome, le nombre d'électron de l'atome. C'est encore le nombre de charges. Quelle est la configuration électronique du chlore dans son état fondamental ? 1s2 2s2 2p6 3s2 3p5. Dans quelle colonne de la classification périodique se situe le chlore ? Comment se nomment les éléments de cette colonne ? Le chlore appartient  à la famille des halogènes, colonne 17 ( VII A)  Faire les schémas des structures de Lewis les plus probables des molécules de dichlore et de chlorure d’hydrogène (HCl). Donner dans les deux cas les nombres d’oxydation du chlore. Dans HCl, le nombre d'oxydation du chlore vaut -1 et dans Cl2, le nombre d'oxydation du chlore est nul. Qu’est ce qu’un nucléon ? Un nucléon est un constituant du noyau de l'atome, c'est à dire un proton ou un neutron. Rappeler la définition de deux isotopes d’un même élément. Deux isotopes possèdent le même nombre de protons ( même numéro atomique) mais des nombres de neutrons différents. Le chlore a une masse atomique molaire moyenne d’environ 35,5 g.mol-1. Il est essentiellement composé des isotopes 35 et 37. La masse molaire d’un nucléon est prise à 1 g.mol-1. Déterminer la proportion molaire de chaque isotope. On note x la proportion molaire de l'isotope 35 et 1-x celle de l'isotope 37. 35x +(1-x)37 = 35,5 -2x +37 = 35,5 ; x = 1,5/2 : 0,75 Chlore 35 : 75 % ; chlore 37 : 25 %. Chlorure d’hydrogène. Le chlorure d’hydrogène HCl(g), très soluble dans l’eau est entièrement dissocié en solution aqueuse. Ecrire la réaction de dissolution. Quel nom donne-t-on à cette solution ? HCl(g) + H2O(l) = H3O+aq + Cl-aq. Il s'agit d'une solution d'acide chlorhydrique. Sous la pression de 1 bar à 15°C, on peut dissoudre au maximum 500 L de chlorure d’hydrogène (gaz supposé parfait) dans 1 L d’eau. Cette dissolution se fait avec changement de volume du liquide. On obtient une solution S0 dont la masse volumique est 1,2 kg.dm-3. Quelle est la concentration molaire volumique de la solution d’acide obtenue ? La loi des gaz parfaits conduit à : n = PV /(RT) = 105*0,5 / (8,31*288)=20,88 mol de chlorure d'hydrogène. Masse de chlorure d'hydrogène : m = 20,88 *36,5 =762,2 g. Masse d'eau dans la solution S0 : 1000 g ; masse totale de la solution S0 : 1762,2 g. % massique de HCl dans cette solution :762,2*100/1762,2 = 43,2 % masse d'un litre de cette solution : 1200 g ; masse de HCl dans 1 litre de cette solution : 1200*0,432 =519 g Concentration de la solution S0 : 519 / 36,5 =14,2 mol/L~14 mol/L. Equilibre chimique en phase gazeuse.  Sous la pression P0 = 1 bar maintenue constante, à la température T, à partir d’un mélange de HCl(g) et de O2(g), il se forme Cl2(g) et H2O(g). Ecrire l’équation bilan de la réaction avec 1 pour coefficient (nombre) stoechiométrique de O2. 4HCl(g) +O2(g) = 2Cl2(g) +2H2O(g). Les réactifs sont pris en quantités stoechiométriques (1 mole de O2). Quel est l’avancement maximum xmax de cette réaction ? Dans le cas d'une réaction totale, les deux réactifs disparaissent en fin de réaction : xmax = 1 mol. A l’équilibre, 75% de HCl a disparu.  Déterminer l’avancement xe de la réaction à l’équilibre. avancement (mol) 4HCl(g) +O2(g) = 2Cl2(g) +2H2O(g) initial 0 4 1 0 0 en cours x 4-4x 1-x 2x 2x à l'équilibre xe 4-4xe =1 1-xe=0,25 2xe =1,5 2xe=1,5 75 % de 4 mol  de HCl (g)  a disparu  à l'équilibre : il en reste donc 4*0,75 = 1 mol. Par suite : 4-4xe =1 soit xe =0,75 mol.  Les gaz étant supposés parfaits, déterminer les pressions partielles de chacun des constituants à l’équilibre. Nombre total de moles  à l'équilibre : N = 4,25 moles. Fractions molaires : XHCl =1/4,25 =0,235 ; XO2 =0,25/4,25 =0,059 ; XCl2 =XH2O =1,5/4,25 =0,353. Pressions partielles : PHCl =XHCl P0 =0,235 bar ; PO2 =XO2 P0 = 0,059 bar ; PCl2 =PH2O =XCl2 P0=0,353 bar.  Exprimer la constante de cet équilibre K0P à la température T en fonction des pressions partielles et la calculer. K0P=P2Cl2 .P2H2O / ( PO2.P4HCl) = 0,3534 / (0,059 *0,2354) =86,3 ~ 86.   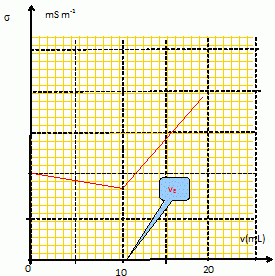Web www.chimix.com Dosage des ions chlorure Cl-(aq) par précipitation. Dans cet exercice, tous les ions sont sous forme aqueuse. Pour s’assurer que le dosage des ions Cl-(aq) par les ions Ag+(aq) est possible, on réalise au préalable la manipulation suivante. On effectue le dosage de V1 = 100 mL d’une solution S1 placée dans le bécher, de chlorure de sodium (Na+, Cl-) de concentration C1 = 10-2 mol.L-1 par une solution S2 de nitrate d’argent (Ag+, NO3-) placée dans la burette, de concentration C2 = 8.10-2 mol.L-1. Le produit de solubilité du chlorure d’argent AgCl(s) est : K0S1 =10-10. Ecrire la réaction de dosage. Ag+(aq) + Cl-(aq) = AgCl(s). Exprimer la constante d’équilibre K en fonction des concentrations. K = 1/ ([Ag+(aq)][Cl-(aq)]) =1/ K0S1 = 1010.  La précipitation débute-t-elle dès la première goutte ? (une goutte = 0.05 mL). La précipitation  débute dès que le produit de solubilité est atteint :  [Cl-(aq)]i =C1 = 10-2 mol.L-1. Juste après l'ajout de la première goutte : [Ag+(aq)]i = (8 10-2  *0,05 / 100) = 4 10-5 mol/L. [Cl-(aq)]i [Ag+(aq)]i = 4 10-7 , valeur supérieure au produit de solubilité : la précipitation a débuté. Calculer le volume V2e de la solution de nitrate d’argent versé à l’équivalence. C2V2e =V1 C1 ;  V2e =V1 C1/C2 =100*10-2 /8.10-2= 12,5 mL ~ 13 mL. On a ajouté dans le bécher, en guise d’indicateur coloré, V3 = 2 mL d’une solution de chromate de potassium K2CrO4, (2 K+, CrO42-) de concentration C3 = 1 mol.L-1, susceptible de donner le précipité Ag2CrO4(s), de couleur rouge, dont le produit de solubilité est  K0S2 =10-11,8. Ecrire la réaction de précipitation de Ag2CrO4(s). Ag2CrO4(s) = 2Ag+ aq+ Cr042- aq ; Exprimer la constante d’équilibre K0S2 en fonction des concentrations. K0S2 = [ Ag+ aq]2[ Cr042- aq]  Montrer que AgCl(s) précipite avant Ag2CrO4(s). AgCl(s) = Ag+ aq+ Cl- aq; K0s1 = [ Ag+ aq][ Cl- aq] avec [ Cl- aq]initial = 10-2 mol/L. AgCl commence à précipiter dès que [ Ag+ aq] = K0s1 / [ Cl- aq]initial = 10-10 / 10-2 =  10-8 mol/L Ag2CrO4(s) = 2Ag+ aq+ Cr042- aq ; K0S2 = [ Ag+ aq]2[ Cr042- aq]  avec [ Cr042- aq]initial =C3V3/ (V3+V1)=2/102= 1,96 10-2 mol/L Ag2CrO4 commence à précipiter dès que [ Ag+ aq] =[ K0S2 / [ Cr042- ]initial ]½=[ 10-11,8 / 1,96 10-2 ]½ = 9 10-6 mol/L AgCl précipite donc en premier. Quelle est la concentration en ions Cl- dans le bécher quand Ag2CrO4(s) commence à précipiter. (On considérera que le volume est très voisin de celui à l’équivalence). [ Cr042- aq]éq =C3V3/ (V3+V1+V2e)=2/114,5= 1,74 10-2 mol/L. Ag2CrO4 commence à précipiter dès que [ Ag+ aq] =[ K0S2 / [ Cr042- ]initial ]½=[ 10-11,8 / 1,74 10-2 ]½ = 9,5 10-6 mol/L. [ Cl- aq] =K0s1 / [ Ag+ aq] = 10-10 / 9,5 10-6 =1,0 10-5 mol/L. Le titrage précédent est maintenant réalisé par conductimétrie. Quelle est la grandeur physique mesurée ? On mesure la conductance G ( S) ou la conductivité s ( S m-1) de la solution.  Rappeler les différentes façons d’obtenir des courbes formées de segments de droites. Travailler  à volume pratiquement constant : solution titrée de grand volume et solution titrantre  assez concentrée. On reorésente la conductivité en fonction du volume de solution titrante. Sinon il faut prendre en compte la dilution et représenter  : s V / (V+v) = f(v) avec s : conductivité ; V : volume de la solution titrée et v : volume de la solution titrante.  On donne les conductivités molaires limites ioniques suivantes (en mS.m2.mol-1) : λ°(Cl-) = 7,6 ; λ°(Ag+) = 6,2 ; λ°(NO3-) = 7,1 ; λ°(Na+) = 5,0.  Exprimer la conductivité d’une solution ionique en fonction des concentrations et des conductivités molaires ioniques des ions. s = λ°(Cl-) [Cl-] + λ°(Ag+) [Ag+] + λ°(NO3-) [NO3-] + λ°(Na+)[Na+] Les concentrations s'expriment en mol m-3. Expliquer de façon simple comment varie la conductivité de la solution contenue dans le bécher au cours du titrage et tracer l’allure de la courbe du titrage conductimétrique précédent. Avant l'équivalence : Du point de vue de la conductimétrie, tout se passe comme si on remplaçait l'ion chlorure par l'ion nitrate : λ°(NO3-) est un peu inférieure  à λ°(Cl-) ; la conductivité de la solution diminue faiblement. Après l'équivalence : On ajoute des ions argent Ag+ et des ions nitrate  NO3-: la conductivité de la solution augmente assez rapidement. Cinétique. Soit la réaction d’hydrolyse, en solution aqueuse, d’un chlorure d’alkyle noté RCl  : RCl + H2O → ROH + H+(aq) + Cl-(aq) Un bécher contient V0 = 250 mL d’eau et un indicateur coloré jaune en milieu acide et bleu en milieu basique. Au dessus, se trouve une burette contenant une solution aqueuse d’hydroxyde de sodium (ou soude Na+(aq), HO-(aq) ) concentrée. On considérera dans ce problème que le volume dans le bécher reste V0. A l’instant t = 0 min, on verse dans le bécher n = 5.10-4 mol de soude et une quantité de RCl, qui amène sa concentration initiale dans le bécher à une valeur « a » telle que a = 1,1.10-2 mol.L-1. On notera x la concentration en ROH à l’instant t. A l’instant t1, la couleur jaune apparaît. On note t1 et on verse à nouveau n = 5.10-4 mol de soude dans le bécher. La couleur jaune réapparaît à l’instant noté t2. On répète encore 3 fois l’opération et on note t3, t4 et t5. Expliquer ces changements de couleur. L'hydrolyse du chlorure d'alkyle libère des ions oxonium H+(aq) ; ceux-ci réagissent avec les ions hydroxyde HO-(aq) ajoutés  ( réaction acide base rapide ). Lorsque tous les ions hydroxydes ont réagi, l'hydrolyse libérant  des ions oxonium, la couleur jaune réapparaît. La cinétique de cette réaction étant d’ordre 1 par rapport à RCl, exprimer la loi de vitesse, en déduire une équation différentielle en x, l’intégrer et exprimer la concentration x en fonction de a, de t et de la constante de vitesse k. 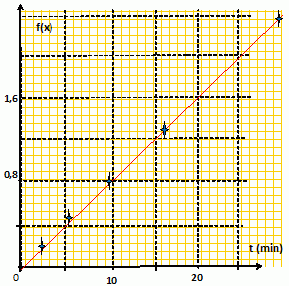avancement (mol) RCl +H2O ROH + H+(aq) + Cl-(aq) t=0 0 aV0 solvant 0 0 0 t1 n aV0 -n en grand n n n t2 2n aV0 -2n excès 2n 2n 2n [ROH]= x = i n/ V0 ; [RCl]= (aV0 - i n)/ V0 =a-x v =k[RCl] = -d[RCl]/dt avec [RCl] = a-x et [ROH]=x ; -d[RCl]/dt = dx/dt k(a-x) = dx/dt ; dx / (a-x) = kdt ; -d(a-x) / (a-x) = kdt Intégrer entre 0 et t : -ln(a-x) = - kt + constante ; à t = 0 x=0 et la constante vaut -ln a d'où ln [(a-x) / a ]= -kt. Quelle fonction f(x) doit-on tracer pour différentes valeurs de t si l’on veut obtenir une droite de pente +k ?  Tracer ln([a /(a-x) ]  en fonction du temps. Le tableau ci-dessous donne les différentes valeurs des ti. Reproduire et compléter ce tableau. ti min t0 = 0 t1 = 2,5 t2 = 6 t3 = 10 t4 = 16,5 t5 = 30 xi 0 5 10-4 / 0,25 =2.10-3 4.10-3 6.10-3 8.10-3 10.10-3 f(xi) 0 0,20 0,45 0,79 1,3 2,4 k = f(xi) / ti min-1 xxxxxxxxxx 0,080 0,075 0,079 0,079 0,080 Placer les couples de points (f(xi), ti ) sur un graphe (tracé sur la feuille). Leur alignement est-il satisfaisant ? Déduire la valeur de la constante de vitesse k en précisant bien son unité. La dernière ligne du tableau donne la valeur de k ainsi que son unité : k = 0,079 min-1. L'écart relatif entre les valeurs de k est  de : (0,080-0,075) / 0,079 = 0,06 ( 6 %) Si on ignore la valeur  s'écartant le plus des autres, l'écart relatif est de : (0,080-0,079) / 0,079 = 0,01 ( 1 %)

retour -menu