Cycle moteur théorique et peu performant.
Données numériques : VB = 1 L, VA = 330 mL, T0 = 300 K, P0 = 1 bar, m = 10 kg, S = 100 cm². g = 10 N.kg-1. γ = 1,4. La constante des gaz parfaits est : R = 8,314 J.K-1.mol-1. Les capacités thermiques du gaz seront supposées indépendantes de la température. On rappelle que : R = Cpm-Cvm et g=Cpm/Cvm avec : Cpm et Cvm : capacités thermiques molaires, respectivement à pression et à volume constants du gaz.
Les différentes transformations seront supposées réversibles.
On imagine un cylindre aux parois diathermanes (perméables à la
chaleur), fermé par un piston. Le piston, de masse négligeable, peut
glisser sans frottement entre 2 cales A et B, sa section est S.
Dans l’état initial, le piston est en A, le cylindre renferme un volume VA d’air supposé gaz parfait, de coefficient γ, à la température de l’extérieur : T0, pression P0, (gaz dans l’état 0 : P0,VA,T0)
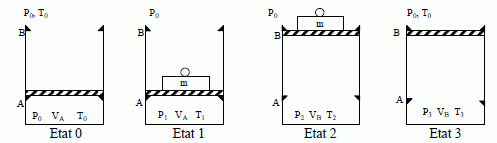
On
place une masse m sur le piston et on chauffe très doucement le gaz par
un moyen approprié, non représenté sur le schéma, jusqu’à ce que le
piston décolle juste de la cale A (gaz dans l’état 1 : P1, VA, T1).
Puis, on maintient le chauffage jusqu’à ce que le piston arrive juste en B (gaz dans l’état 2 : P2,VB,T2), le chauffage est alors arrêté.
On ôte m et on laisse refroidir l’ensemble jusqu’à ce que le piston décolle juste de B (gaz dans l’état 3 : P3, VB, T3).
On laisse toujours refroidir jusqu’à la température T0, alors, le piston revient en A (gaz dans l’état 0), le cycle est terminé.
Exprimer les capacités thermiques à pression et à volume constants Cp et Cv du gaz en fonction de n (quantité de matière de gaz enfermé), R, γ, puis en fonction de P0, VA, T0, γ.
Cp = n Cpm ; Cv = n Cvm ;
R = Cpm-Cvm = gCvm-Cvm ; Cvm=R / (g-1) ; Cpm=gR / (g-1) ;
Cp = ngR / (g-1) ; Cv = nR / (g-1).
L'équation des gaz parfaits s'écrit pour le gaz dans l'état 0 : P0 VA=nRT0 ; nR= P0 VA / T0.
Cp = P0 VA g / ((g-1)T0) ; Cv = P0 VA / ((g-1)T0).
|
Quelle est la nature de la transformation de 0 à 1 subie par le gaz ?
Le volume du gaz reste constant ; la transformation est isochore.
|
Exprimer la pression P1 et la température T1 en fonction de P0, T0, m, g, S. Faire l’application numérique.
L'équation des gaz parfaits s'écrit pour le gaz dans l'état 1 : P1 VA=nRT1 ; nR / VA = P0 / T0.
Par suite : P1 = P0 T1 / T0 soit T1 = P1T0 /P0.
De plus P1 = P0+mg / S ; T1 = ( P0+mg)T0 /(SP0).
S = 100 cm² = 1,0 10-2 m2 ; P1 =105+ 10*10/ 10-2 =1,1 105 Pa.
T1 = P1T0 /P0 =1,1 105 *300/ 105 = 330 K.
Exprimer la quantité de chaleur (transfert thermique) Q01 reçue par le gaz au cours de cette transformation en fonction de Cv ou Cp, T1, T0 puis P0, T1, T0, VA, γ. Faire l’application numérique.
Q01 =Cv (T1- T0 ) ; or Cv = nR / (g-1) et nR = P0VA / T0.
Q01 =P0VA (T1- T0 )/ (T0(g-1)).
Q01 = 105*3,3 10-4*30/ ( 300*0,4) = 8,25 J~8,3 J.
Quelle est la nature de la transformation 1 à 2 subie par le gaz ?
La pression reste constante égale à P1 ; la transformation est isobare.
Exprimer la température T2 en fonction de T1, VA, VB. Faire l’application numérique.
L'équation des gaz parfaits s'écrit pour le gaz dans l'état 2 : P1 VB=nRT2 ; nR / P1 = VA / T1.
VB=T2 VA / T1 ; T2 =T1 VB / VA =330*1 / 0,33 =1000 K.
Exprimer la quantité de chaleur (transfert thermique) Q02 reçue par le gaz au cours de cette transformation en fonction de Cv ou Cp, T1, T2 puis P0, T1, T0, T2, VA, γ. Faire l’application numérique.
Q02 =Cp (T2- T1 ) ; or Cp = nRg / (g-1) et nR = P0VA / T0.
Q02 =P0VA (T2- T1 )g/ (T0(g-1)).
Q02 = 105*3,3 10-4*670*1,4/ ( 300*0,4) = 257,95 J~258 J.
Quelles sont les natures des transformations 2 à 3 et 3 à 0 subies par le gaz ?
Le volume du gaz reste constant ; la transformation 2 à 3 est isochore.
La pression reste constante égale à P0 ; la transformation est 3 à 0 est isobare.
Exprimer le travail W échangé par ce « moteur » avec l’extérieur, au cours du cycle, en fonction de m, g, VA, VB, S. Faire l’application numérique.
Le travail fourni par le gaz au cours de la transformation 0 à 1 est nul : il y a une butée en A et le piston ne se déplace pas.
Force pressante exercée par le gaz au cours de la transformation 1 à 2 : F =P1 S.
Le piston se déplace d'une longueur : h = (VB-VA) / S.
Travail de cette force : P1(VB-VA) ; le gaz fournit au milieu extérieur le travail : -P1(VB-VA)
Le travail fourni par le gaz au cours de la transformation 2 à 3 est nul : il y a une butée en B et le piston ne se déplace pas.
Force pressante exercée par l'air extérieur au cours de la transformation 3 à 0 : F =P0 S.
Le piston se déplace d'une longueur : h = (VB-VA) / S.
Travail de cette force : P0(VB-VA) ; le gaz reçoit le travail : P0(VB-VA)
Travail fournit par le gaz au cours du cycle : W = (P0-P1)(VB-VA).
W= - 104(1-0,33) 10-3 = -6,7 J.
Exprimer le rendement de ce « moteur » en fonction des différents transferts d’énergie. Faire l’application numérique.
Le rendement est égal au travail fournit au milieu
extérieur par le gaz divisé par l'énergie dépensée pour chauffer
le gaz.
|W| / (
Q01+
Q02).) = 6,7 / (8,3+258) =0,025 ( 2,5 %)
Tracer l’allure du diagramme de Clapeyron d’un cycle.
Retrouver, d’après le diagramme, le travail W calculé précédemment.
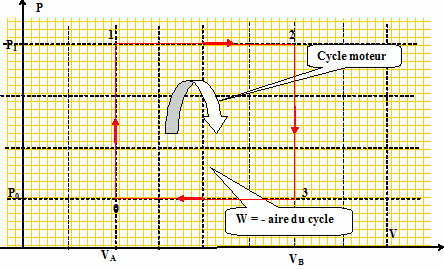
W = (P0-P1)(VB-VA).
Exprimer le rendement d’un moteur fonctionnant selon un cycle de Carnot entre les températures T0 et T2 puis le calculer.
h=1-T0/T2 = 1-300/1000 = 0,7 (70%)
|
Le
schéma suivant, représente, en coupe, un réservoir R, un cylindre C
(leurs parois sont diathermanes, c'est-à-dire perméables à la chaleur)
et un piston P dont la course est limitée par le fond A et la cale B.
Quand le piston est en A, le volume du cylindre limité par le piston
est VA, quand il est en B : VB. Le système est de plus, muni de deux soupapes : S1 permettant le passage du gaz uniquement de C vers l’extérieur et S2
uniquement de R vers C, et ce, dès que la différence de pression entre
les parties inférieure et supérieure de la soupape est positive. Le
cylindre est relié, par un tube de volume négligeable devant les autres
volumes du système, au réservoir R de volume V0, très supérieur à VB, contenant de l’air, supposé gaz parfait, dans lequel on souhaite «faire le vide ».
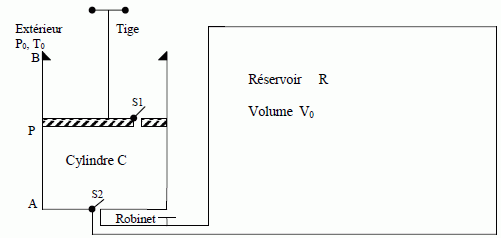
Dans l’état initial, le piston est en B, le cylindre et le réservoir contiennent de l’air à la pression atmosphérique P0 et à la température T0. On pousse le piston jusqu’en A exactement contre le fond (on considère qu’ici VA = 0) et on le ramène en B assez lentement pour que la température reste T0.
Expliquer les différents transferts de gaz au cours de cet aller-retour.
En poussant le piston jusqu'en A, la pression augmente dans le cylindre C : la soupape S1 s'ouvre, S2 se ferme et le cylindre C se vide d'air.
Quand on déplace le piston de A vers B, la soupape S1 se ferme et la soupape S2 s'ouvre ; de l'air passe du réservoir dans le cylindre.
Montrer que la pression P1 dans R quand le piston revient en B est : P1 =P0V0 /(V0+VB).
La transformation est isotherme ; l'air est considéré comme un gaz
parfait. La masse d'air dans le réservoir et le cylindre est constante
quand le piston monte de A en B.
La loi de Mariotte conduit à : P0V0 =P1(V0+VB).
Si les transferts de gaz s’effectuent encore de la même façon, exprimer littéralement la pression P2 après un deuxième aller-retour du piston.
La transformation est isotherme ; l'air est
considéré comme un gaz parfait. La masse d'air dans le réservoir et le
cylindre est constante quand le piston monte de A en B.
La loi de Mariotte conduit à : P1V0 =P2(V0+VB) ;
P2 =P1V0 /(V0+VB) =P0 [V0 /(V0+VB)]2.
Donner, dans ce cas, la forme générale de Pn après le nième aller-retour. Quelle est la limite de Pn quand n → ∞ ?
Pn =P0 [V0 /(V0+VB)]n = P0 [1 /(1+VB/V0)]n ~ P0 [1-nVB/V0]
La pression tend vers zéro dans le réservoir si n tend vers l'infini.
En réalité, quand le piston est en A, le volume VA entre le piston et le fond n’est pas nul. La limite théorique précédente ne peut pas être atteinte.
Pourquoi ? Déterminer la véritable limite théorique de cette pompe à vide. Pourquoi appelle-t-on VA le « volume nuisible »?
La soupape S1 étant fermée dès que le piston remonte, la soupape S2 s'ouvre dès que la pression dans le réservoir est supérieure à la pression dans le piston.
Quand le réservoir est pratiquement vide, lors de la montée du piston :
Ecrire la loi de Mariotte pour le gaz compris dans le piston :
piston en A : P0VA = constante.
piston en B : PnVB = constante d'où Pn =P0VA /VB.
Si la pression dans le réservoir est inférieure à P0VA /VB la soupape S2 ne s'ouvre pas.
L'espace qui reste entre le bas de la course du piston et la soupape S2 est préjudiciable à l'aspiration du gaz du réservoir : on le nomme espace nuisible.
Quel est, en supposant disposer d’une pompe idéale (VA = 0), le travail théorique minimum nécessaire pour faire le vide parfait dans R ?
Le travail de l'opérateur est opposé au travail des forces pressantes.
dW = PdV ; or PV = constante : PdV = -VdP
dW = -VdP ; le volume du réservoir est constant égal à V0 et la pression varie de P0 à 0 dans le réservoir :
W = V0P0.
|
|


