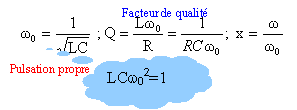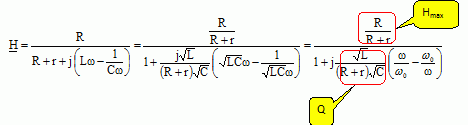Bobine inductive, dipôle RLC, fonction de transfert, facteur de puissance : concours Mines 2009.

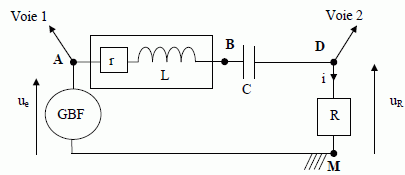
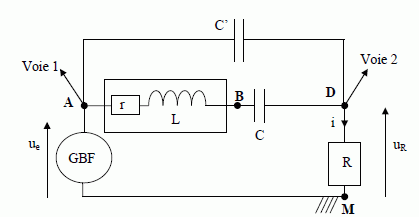
On dispose  d'une bobine B que l'on assimilera  à l'association en série d'une inductance L et d'une résistance r ( L et r sont des constantes positives indépendantes de la fréquence). Détermination de r. La bobine est parcourue par un courant  i(t). Exprimer la tension u(t) à ses bornes en fonction  de r, L, i(t) et de sa dérivée par rapport au temps. 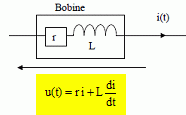On réalise le circuit suivant, en plaçant, en série avec la bobine, un résistor de résistance R = 40 Ω. L’alimentation est un générateur de tension continue, constante, de force électromotrice E0 = 1,0 V et de résistance interne r0 = 2,0 Ω. 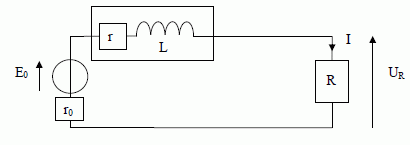On mesure, en régime permanent, la tension UR aux bornes  de R. Exprimer r en fonction  des données de cette question. Calculer r avec UR = 0,56 V. En régime permanent l'intensité I est constante ( la dérivée de I par rapport au temps est nulle dI/dt =0 ) : la tension aux bornes de la bobine  est égale  à  : Ubob = r I. Additivité des tensions : E0-r0I = rI +UR ; de plus UR =RI soit I = UR /R. Par suite : E0-r0 UR /R = r UR /R +UR ; r = (R E0 -RUR -r0 UR)  /UR  =R E0 /UR-R -r0 =40*1,0 /0,56-40-2,0 =29,4 ~ 29 Ω.  Détermination de r et L  à partir d'un oscillogramme. On place, en série avec la bobine, un résistor de résistance R = 40 Ω et un condensateur de capacité C = 10 μF . Le GBF (générateur basses fréquences) est réglé pour délivrer une tension sinusoïdale de fréquence f = 250 Hz (la pulsation sera notée ω) et de valeur crête à crête de 10 V. Deux tensions sont visualisées sur un oscilloscope numérique. 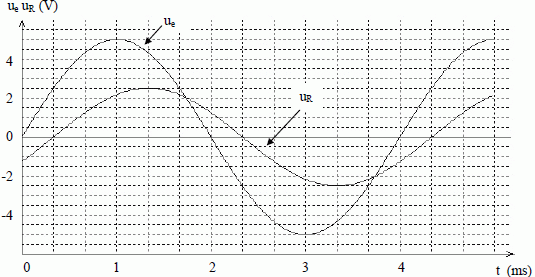On obtient un oscillogramme équivalent au graphe suivant : Déterminer l’amplitude Ue de la tension ue et l’amplitude UR de la tension uR. Ue = 5 V ; UR = 2,5 V. Déterminer l’amplitude I du courant i. I = UR /R = 2,5/40 =0,0625 A ~ 6,3 10-2 A. Rappeler l’expression générale de l’impédance Z d’un dipôle quelconque (module de l’impédance complexe). Calculer alors l’impédance ZAM du dipôle AM. Z = R + jX ; ZAM = Ue / I = 5 / 0,0625  = 80 Ω. Des deux tensions, uR(t) et ue(t), laquelle, et pourquoi d’après l’oscillogramme, est en avance sur l’autre ? Lorsque les deux tensions varient dans le même sens, celle qui est en avance  passe en premier par un maximum ou par une valeur nulle. ue est en avance sur uR, c'est  à dire sur l'intensité ( uR et l'intensité étant proportionnelles ). Déterminer précisément, à partir de l’oscillogramme, le déphasage ϕue/i entre ue et i, (c’est-à-dire entre ue et uR). Le décalage des deux courbes est de  une division, alors que la période correspond  à 12 divisions. Une période correspond  à 2 pi radians, d'où : ϕue/i  = 2 pi /12 = pi / 6 = 0,52 radian.  Ecrire l’expression générale de l’impédance complexe ZAM en fonction de r, R, L, C, ω. ZAM = R+r + j(Lω-1/(Cω ) )  Ecrire l’expression de l’impédance complexe ZAM en fonction de son module ZAM et du déphasage ϕue/i. ZAM = ZAM exp (jϕue/i) Exprimer r en fonction de R, ZAM et ϕue/i. Calculer sa valeur. r+R = ZAM cos ϕue/i ;  r = ZAM cos ϕue/i -R = 80 cos (pi/6) -40 =29,3 ~ 29 Ω. Exprimer L en fonction de C, ω, ZAM et ϕue/i. Calculer sa valeur. Lω-1/(Cω ) = ZAM sin ϕue/i ; Lω = ZAM sin ϕue/i +1/(Cω ) L = [ZAM sin ϕue/i +1/(Cω )] / ω  ; ω =2 pi f = 2*3,14*250 =1570,8 rad/s ; Cω =10-5*1570,8 =0,0157 ; 1/(Cω ) =63,66 ohms. L = [80 sin (pi/6)+63,66] / 1570,8 =0,066 H.     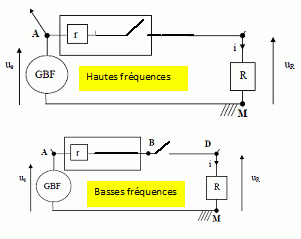Fonction de transfert.  Rappeler la définition de la fonction de transfert H du filtre  avec ue pour tension d'entrée et uR pour tension de sortie. H = uR / ue Proposer un schéma équivalent en basses puis en hautes fréquences et en déduire la nature probable du filtre. En hautes fréquences le condensateur se comporte comme un interrupteur fermé et  la bobine comme un interrupteur ouvert. En basses fréquences le condensateur se comporte comme un interrupteur ouvert et la bobine comme un interrupteur fermé  ( si r est très faible) Le filtre est un filtre passe bande. Exprimer H en fonction de r, R, L, C, w. toutes les grandeurs soulignées sont des nombres complexes. A ces grandeurs on peut appliquer les lois du courant continu Le pont diviseur de tension conduit à :  H = uR / ue La figure ci-dessous représente le diagramme de Bode du filtre précédent. Rappeler la définition du diagramme de Bode. Le diagramme logarithmique de Bode représente le comportement en fréquence d'un quadripole. 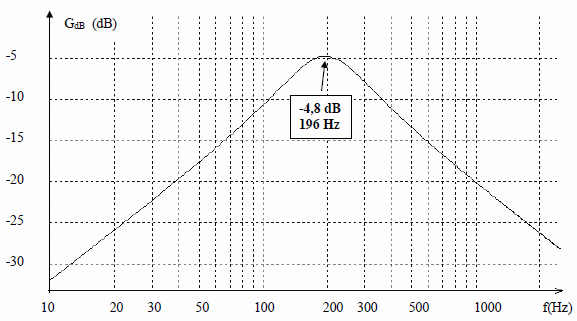Il s'agit de la représentation graphique de la fonction : g = 20 log H(w) Déterminer, à partir du graphe et des données initiales, les valeurs de r et L. LCw02=1 ; avec w0 = 2 pi f0 =2*3,14*196 =1231 rad/s. L = 1/ (Cw02)= 1 / (10-5*12312) =0,066 H. H (w = w0 ) =R / (R+r) ; H(w = w0 ) = Hmax ; log Hmax = log (R/R+r) ; 20 log (R/R+r) = -4,8 ; log[(R +r)/R] = 4,8 /20 =0,24 ; (R+r) / R =100,24 = 1,738 ; r = 0,738 R = 0,738*40 = 29 ohms.     Facteur de puissance. f = 250 Hz. Rappeler la définition du facteur de puissance. L'intensité du courant et la tension aux bornes du dipôle étant des fonctions sinusoïdales, le facteur de puissance est égal au cosinus du déphasage entre la tension et l'intensité. C'est le rapport  entre la puissance active P  consommée et la puissance apparente S. On place en parallèle sur AD une boîte de condensateur à décades et l'on fait varier la capacité C' jusqu'à ce que, en observant  à l'oscilloscope, uR et ue soient en phase. Quelle est la valeur du facteur de puissance du circuit AM ? Intensité et tension aux bornes du circuit étant en phase, le déphasage est nul entre tension et intensité : cos j = 1. Quelle est alors la valeur du facteur de puissance du circuit AD ? Quelle particularité présente alors l'admittance complexe YAD du circuit AD ? L'admittance  YAD est un nombre réel et sa valeur est maximale. Le facteur de puissance  du circuit AD vaut 1. Exprimer YAD en fonction de r, L, C, C' et de la pulsation w. Déterminer C' en fonction de r, L, C et w. Faire l'application numérique. w = 2 pi f = 6,28*250 =1570 rad/s ;  A = Lw-1/(Cw) = 0,066*1570-1/(10-5*1570) =40 ohms. C' = 40 / [1570 (292+402)]=1,0 10-5 F.

retour -menu