Glucose, stéréoisomères, inversion du saccharose, chimie concours Mines 08

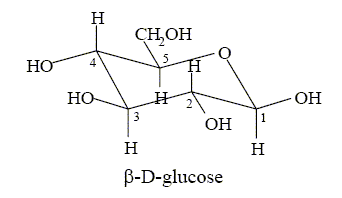
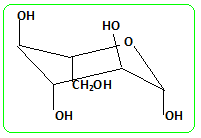
Il s’agit de la manière la plus simple d’obtenir des biocarburants. Le jus sucré (issu de betteraves ou de cannes à sucre) est mis à fermenter dans une cuve puis distillé afin d’en réduire la teneur en eau. On s’intéresse à l’exemple du saccharose. La production se fait en deux étapes. Hydrolyse ou inversion du saccharose (enzyme : invertase) C12H22O11 + H2O = glucose + fructose. Fermentation du glucose : en l’absence de dioxygène C6H12O6 = 2 C2H5OH + 2 CO2. On se propose d’étudier la molécule de glucose puis la cinétique de sa fermentation en relevant les quantités d’éthanol gazeux dégagé. On utilise ici de la levure de boulanger qu’on met en suspension dans un tampon phosphate de pH égal à 6,2. La molécule de glucose. 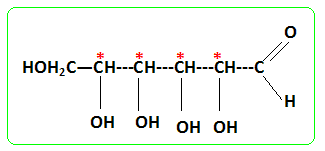Le ß D-glucose dont la strcture est donnée ci-dessous est la forme hémiacétal cyclique d’un des diastéréoisomères du pentahydroxy-2,3,4,5,6-hexanal : Étude de la forme linéaire du glucose : Dans l’étude qui suit, les structures des molécules pourront être données soit par des formules semi-développées soit par des représentations topologiques. Donner la structure du pentahydroxy-2,3,4,5,6-hexanal. Repérer ses atomes de carbone asymétriques par une *. En déduire le nombre de stéréoisomères de configuration de la molécule. Qu’appelle-t-on des « diastéréoisomères » ? 4 atomes de carbone asymétriques soit 24 stéréoisomères de configuration. 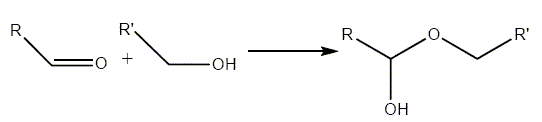« diastéréoisomères » : encore stéréoisomères qui ne sont pas des énantiomères. Étude d’un des deux stéréoisomères cycliques du glucose. La forme linéaire du glucose est en équilibre avec sa forme cyclique. Cet équilibre chimique est basé sur la réaction dite d’acétalisation de l’aldéhyde. 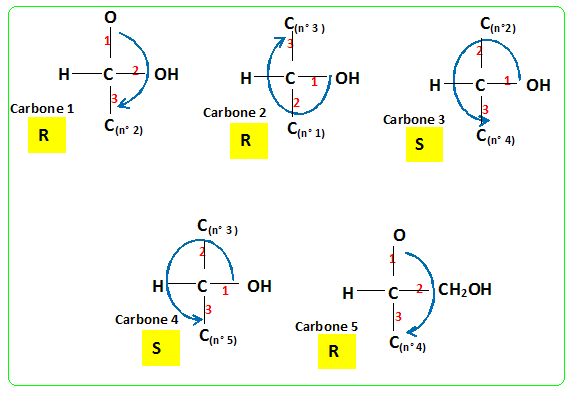La forme générale de cette réaction pour un aldéhyde et un alcool primaire est : Déterminer les configurations absolues des atomes de carbone asymétriques du ß-D-glucose dont la structure a été donnée précédemment. On s’intéresse au ß-D-glucose. Dessiner l’autre conformère de cette molécule (cycle en conformation chaise). Indiquer, en justifiant, lequel des deux conformères est le plus stable. Les substituants les plus encombrants étant en position axiale, cette conformation est moins stable que celle proposée, dans laquelle les plus gros substituants sont en position équatoriale. Étude de la réaction d’inversion. Le saccharose est constitué d’une molécule de glucose et d’une molécule de fructose reliées entre elles. En présence d’eau et d’acide, la liaison se rompt. L’équation de la réaction est schématisée ci-après : C12H22O11 (saccharose) + H2O = glucose (C6H12O6) + fructose (C6H12O6). Les pouvoirs rotatoires spécifiques sont notés [a]G, [a]F, [a]S, respectivement pour le glucose, le fructose et le saccharose, d’unités °.dm-1.g-1.L. Le volume de la solution est constant. On rappelle la loi de Biot : a = S[a]i l Ci. Les concentrations Ci sont données en g.L-1, la longueur de la cuve en dm et l’angle a en degré. Établir l’expression du pouvoir rotatoire total de la solution de saccharose noté a en fonction des pouvoirs rotatoires spécifiques des espèces mises en jeu dans cette réaction, de leurs concentrations et de la longueur de la cuve notée l. a =( [a]G [glucose] + [a]F [fructose] + [a]S [saccharose] ) l. On suppose que la réaction admet un ordre 1 par rapport au saccharose. On appelle x l’avancement volumique de la réaction exprimé en mol.L-1, c0 la concentration initiale en saccharose exprimée en mol.L-1 et k la constante cinétique. Établir une équation différentielle en x. v = -d[saccharose] /dt = k[saccharose] avec [saccharose] = c0 -x d'où : dx/dt = k(c0 -x). On appelle MS la masse molaire du saccharose et MFG la masse molaire du fructose ou du glucose (elles sont égales).   Donner les relations entre les concentrations ci exprimées en mol.L-1 et les Ci en g.L-1. Multiplier les concentrations molaires par les masses molaires respectives : CF = MFG cF ; CG = MFG cG ; CS = MS cS. On appelle a0 le pouvoir rotatoire initial de la solution, a sa valeur à l’instant t et aoo au bout d’un temps infini en considérant la réaction comme totale. Monter que la résolution de l’équation différentielle précédente permet d’obtenir la relation suivante : ln [(aoo -a0) /(aoo -a)] =kt. dx/(C0-x) = kdt ; - ln((C0-x) = kt + cste ; à l'instant initial t=0 : - ln (C0) = cste , d'où : ln(C0/ (C0-x) ) = kt. à l'instant initial : c0 = C0 / MS ; a0 = [a]S C0 / MS l ; à l'instant final : cF oo =cG oo =CF / MFG = C0 / MFG ;aoo = ([a]G + [a]F )C0 / MFG l ; à la date t : a = ([a]G + [a]F )x / MFG l + [a]S (C0-x) / MS l ; Par suite : aoo -a0 = ([a]G + [a]F )C0 / MFG l - [a]S C0 / MS l ; aoo -a0 =C0 [([a]G + [a]F )/ MFG -[a]S / MS ] l ; aoo -a = ([a]G + [a]F )C0 / MFG l - ([a]G + [a]F )x / MFG l - [a]S (C0-x) / MS l ; aoo -a = (C0-x) [ ([a]G + [a]F ) / MFG -[a]S / MS ] l ; soit : (aoo -a0) /(aoo -a) = C0 / (C0-x).

retour -menu