Le fer et ses ions : dosage potentiométrique, chimie concours Mines 08

Les valeurs données sont à 25°C, température de travail. Données : NA= 6,02.1023 mol-1 ; premiers elements chimiques (par Z croissant) : H, He, Li, Be, B, C, N, O, F, Ne, Na, Mg, Al, Si, P, S, Cl, Ar, K, Ca, Sc, Ti, V, Cr, Mn, Fe, Co, Ni, Cu, Zn.... La masse molaire du fer est M = 56 g.mol–1 et sa masse volumique est µ =7,9.103 kg.m–3 en phase solide ; sans préjuger de la structure réelle du cristal, en déduire un ordre de grandeur de la distance entre les noyaux. Quantité de matière (mol) dans 1 m3 de fer solide : 7,9.106 /56 =1,41 105 moles. Nombre d'atomes de fer : 1,41 105 *6,02.1023 =8,49 1028 atomes. Soit [8,49 1028 ]1/3 atomes par mètre ; distance entre deux atomes : 1 / [8,49 1028 ]1/3 = 2,3 10-10 m. Le fer est un métal de transition de numéro atomique Z = 26. Déterminer sa configuration électronique puis sa position dans la classification périodique des éléments. 1s2 2s2 2p6 3s2 3p6 4s2 3d6. ( 4è période et 8è colonne ). Par analyse du spectre d’émission, on détecte dans la couronne solaire des ions Fe13+ (ce qui témoigne d’une température de l’ordre de 106 K !) ; quel est l’élément dont l’atome est isoélectronique de cet ion exotique ? Entre cet atome et l’ion Fe13+, lequel présente le plus grand rayon (à justifier) ? Elément de numéro atomique Z = 13, aluminium. Le noyau de l'atome de fer compte 26 protons positifs, celui de l'aluminium compte 13 protons : l'attraction entre les électrons et le noyau de l'ion Fe13+ est bien plus grande que l'attraction entre le noyau de l'aluminium et ces électrons : l'ion Fe13+ est plus petit que l'atome d'aluminium. Lorsqu’on compare les potentiels rédox standards des couples du type X2+ / X dans la ligne du fer, on constate que celui du manganèse est anormalement bas, ce qui signifie que Mn se transforme plus facilement en X2+ que ses voisins (…24Cr, 25Mn, 26Fe …) ; interpréter ce fait en relation avec les structures électroniques de valence des cations obtenus. Structure électronique de l'ion Fe2+ : 1s2 2s2 2p6 3s2 3p6 3d6. Structure électronique de l'ion Cr2+ : 1s2 2s2 2p6 3s2 3p6 3d4. Structure électronique de l'ion Mn2+ : 1s2 2s2 2p6 3s2 3p6 3d5. Dans ce dernier cas la couche 3 d, à demi complète, est stabilisée. Règle de Hund : quand on a plusieurs O.A de même énergie ( p, d...), il faut occuper le maximum d'OA avec des spins parallèles. Dosage potentiométrique. e = 1,6 10-19 C; E°1(Ce4+/Ce3+) = 1,72 V ; E°1(Fe3+/Fe2+) = 0,77 V. On envisage le dosage potentiométrique des ions fer(II) par des ions cérium(IV) (ions ferreux et ions cériques) : écrire la réaction de dosage. Quelle est la quantité d’électricité échangée pour un avancement de 1 mole ? Ce4+ + e- = Ce3+ ; Fe2+ = Fe3+ + e- d'où : Ce4+ + Fe2+ = Fe3+ +Ce3+. Constante d'équilibre K = [Fe3+]éq[Ce3+]éq/ ([Ce4+]éqFe2]éq) Une mole d'électron est échangée par mole d'ion fer (II) soit 1F = 9,6 104 C. Si l’on prépare un mélange initialement équimolaire en ions ferreux et cériques, quelles relations simples aura-t-on entre les concentrations à l’équilibre des ions fer(II) et cérium(IV) d’une part, fer(III) et cérium(III) d’autre part ? En déduire la valeur du potentiel d’équilibre Eéq. de cette solution, en fonction de E°1 et E°2. On raisonne sur un volume de 1 L. avancement (mol) Ce4+ + Fe2+ = Fe3+ +Ce3+ initial 0 1 1 0 0 équilibre x 1-x 1-x x x [Ce4+]éq = [Fe2]éq ; [Fe3+]éq = [Ce3+]éq. K = [x/(1-x)]2. E1 = E°1 + 0,06 log ([Ce4+] / [Ce3+]) ; E2 = E°2 + 0,06 log ([Fe3+] / [Fe2]) ; E1 éq = E°1 + 0,06 log ([Ce4+]éq / [Ce3+]éq) ; E2 éq = E°2 + 0,06 log ([Fe3+]éq / [Fe2]éq) ; E1 éq =E2 éq ; E°1 + 0,06 log ([Ce4+]éq / [Ce3+]éq) = E°2 + 0,06 log ([Fe3+]éq / [Fe2]éq) ; E°2 -E°1 = 0,06 log K ; log K = (1,72-0,77) / 0,06 =15,83 ; K = 6,8 1015. K est très grande, la réaction est totale, quantitative. K = [x/(1-x)]2 ; x/(1-x) = K½ =8,25 107. E1 éq = E°1 + 0,06 log ([Ce4+]éq / [Ce3+]éq) = 1,72 +0,06 log [(1-x)/x] = 1,72 -0,06 log 8,25 107 = 1,25 V. On dose une solution ferreuse contenant initialement a mol d'ions fer(II) dans un volume V0, par une solution d'ions cérium(IV) de même concentration ; la quantité d'ions cériques apportés a un stade donné du dosage est y.a, avec y appartenant ภ[0,2]. Tout au long du dosage, on mesure la différence de potentiel E' entre une électrode de platine plongeant dans la solution et une électrode de référence au calomel saturée (E.C.S.). En représentant E' = f(y), on obtient une courbe dont l'allure est figurée ci-dessous. On rappelle qu'à 25°C le potentiel de l'E.C.S. par rapport à l'électrode normale à hydrogène vaut 0,25 V. 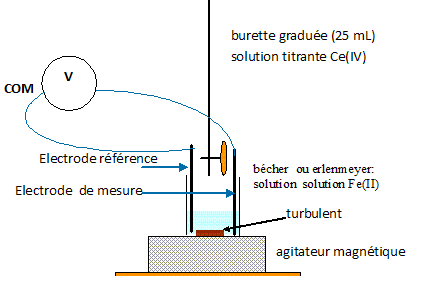Schématiser le dispositif décrit en identifiant clairement les électrodes et la tension mesurée. 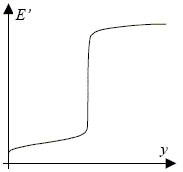Sans nouveaux calculs, donner la valeur du potentiel E’ pour y = 1. En déduire la proportion d’ions ferreux résiduels (non dosés) lorsque y = 1, sous la forme [Fe2+]éq / [Fe2+]0 ; conclure. La quantité de matière d'ion cerrique est égale à la quantité de matière initiale d'ion der (II) : y=1 correspond au point équivalent. E1 éq =1,25 V par rapport à l'électrode à hydrogène ; E' = 1,25-0,25 = 1,0 V par rapport à l'électrode de référence. x/(1-x) = K½ =8,25 107~ 108 soit (1-x) / x = 10-8 ; [Fe2+]éq / [Fe2+]0 = 10-8. La réaction est totale. La courbe obtenue permet un dosage prrècis car le saut de potentiel est important. Comparer les concentrations à l’équilibre des espèces du cérium lorsque y = 2 ; en déduire le potentiel E’ de la solution lorsque y = 2. On raisonne sur un volume de 1 L. avancement (mol) Ce4+ + Fe2+ = Fe3+ +Ce3+ initial 0 2a a 0 0 y=1 x =a 1-x= a 1-x=0 a a y = 2 x = 2a a 0 a a Après l'équivalence, le couple Ce4+ / Ce3+ fixe le potentiel. [Ce4+]=[Ce3+] ; E1 = E°1 + 0,06 log ([Ce4+] / [Ce3+]) ; E1 = E°1 = 1,77 V soit 1,72-0,25 = 1,47 V par rapport à l'électrode de référence. En raisonnant de façon analogue sur les espèces du fer lorsque y = 1/2 ; en déduire le potentiel E’ de la solution lorsque y = 1/2. avancement (mol) Ce4+ + Fe2+ = Fe3+ +Ce3+ initial 0 ½a a 0 0 y=0,5 x =½a 1-x=0 1-x=½a ½a ½a Avant l'équivalence, le couple Fe3+ / Fe2+ fixe le potentiel. [Fe3+]=[Fe2+] ; E2 = E°2 + 0,06 log ([Fe3+] / [Fe2]) ; E2 = E°2 = 0,77 V soit 0,77-0,25 = 0,52 V par rapport à l'électrode de référence. En fait, on mesure E'(y = 1/2) = 0,42 V. Pour interpréter cet écart à la théorie, sachant qu’on travaille en milieu sulfurique et qu’on a utilisé des sulfates (ferreux et cérique), on envisage la formation d’un ion complexe Fe(SO4)+ entre le fer(III) et l’ion sulfate en excès.( remarque : l’ion sulfate complexe aussi les ions fer(II), mais beaucoup plus faiblement et on négligera ce phénomène). On donne pour ce complexe : pKd = 3,85 ; d’autre part, lorsque y = 1/2, la concentration en ions sulfates est voisine de 10–2 mol.L–1. Exprimer E'(y = 1/2) en tenant compte de la complexation du fer(III) et montrer qu’on retrouve effectivement la valeur mesurée. A la demi équivalence [Fe2+]½=[Fe3+]½+[Fe(SO4)+]½ = [Fe3+]½( 1+[Fe(SO4)+]½ / [Fe3+]½) Or Fe(SO4)+ =Fe3+ +SO42- avec Kd =[Fe3+][SO42-] / [Fe(SO4)+ ] par suite [Fe2+]½= [Fe3+]½( 1+ [SO42-] ½/Kd ) = [Fe3+]½(1+0,01/10-3,85 ) =71,8 ;[Fe3+]½ /[Fe2+]½=1/71,8 =0,0139. E2 ( y = 0,5) = E°2 + 0,06 log ([Fe3+]½ / [Fe2]½) = 0,77 + 0,06 log 0,0139 =0,66V soit 0,66-0,25 = 0,41 V par rapport à l'électrode de référence.

retour -menu