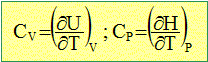Mesures thermodynamiques : calorimètre adiabatique, calorimètre à basse température : physique concours Mines 08

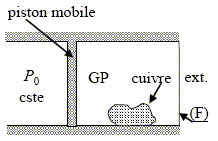
On rappelle que la variation d’enthalpie massique Dh d’un corps pur lors d’un changement d’état physique est aussi appelée « chaleur latente de changement d’état » et notée L. Afin d’éviter les confusions, on notera le temps t, la température absolue T et la température en degrés Celsius q ; pour les applications numériques : T = q + 273,15 Expression du premier principe. Rappeler l’expression du premier principe de la thermodynamique, entre deux états d’équilibre quelconques d’un système fermé globalement immobile dans le référentiel d'étude. Expliquer très simplement la différence entre « travail » et « transfert thermique ». Lors de toute transformation, il y a conservation de l'énergie. Dans le cas des systèmes thermodynamiques fermés : La variation de l'énergie est égale à la quantité d'énergie échangée avec le milieu extérieur, sous forme de chaleur et sous forme de travail.. DU= W+Q. DU : variation d'énergie interne ; W : travail échangé, transfert ordonné ; Q : chaleur échangée, transfert microscopiquement désordonné. On s’intéresse à des systèmes de variables d’état (P, V, T), pour lesquels le seul travail est celui des forces pressantes ; à partir de l’expression précédente, démontrer la relation entre la variation d’enthalpie du système et le transfert thermique dans le cas particulier de transformations isobares. dW = - PdV avec P = constante ; par suite W = -PDV. enthalpie : H = U+PV ; D H = D U +PDV = W + Q + +PDV = -PDV + Q + +PDV ; D H =Q. Calorimétrie adiabatique. Le système étudié, constitué de n moles d’air assimilé à un gaz parfait et d’une masse m de cuivre solide, est contenu dans un cylindre schématisé ci-dessous ; on précise que : • le piston est mobile sans frottement, les autres parois sont fixes ; • les éléments hachurés sont athermanes (i.e. imperméables aux transferts thermiques), tandis que la paroi (F) permet ces tranferts. Coefficient de Laplace du gaz : g = 1,4 ; R = 8,314 J K-1 mol-1 ; n= 1 mole Capacité thermique massique du cuivre : c = 385 J.kg–1.K–1 ; m = 269 g ; P0 est constante ; les valeurs de g et c sont indépendantes de la température. Comment définit-on les capacités thermiques CV et CP d’un système thermodynamique ? Simplifier ces expressions dans le cas du gaz parfait et établir dans ce cas les expressions des capacités molaires CV,M et CP,M en fonction du coefficient g et R. La capacité thermique CV est l'énergie qu'il faut apporter à un corps pour augmenter sa température de un Kelvin, le volume restant constant. La capacité thermique CP est l'énergie qu'il faut apporter à un corps pour augmenter sa température de un Kelvin, la pression restant constante. Elle s'exprime en Joule/Kelvin. C'est une grandeur extensive. Dans le cas d'un gaz parfait : CV m : énergie nécessaire pour élever la température d'une mole de corps pur de 1 kelvin, à volume constant. CP m : énergie nécessaire pour élever la température d'une mole de corps pur de 1 kelvin, à pression constante. L'énergie interne d'un gaz parfait ne dépend que de la température ; l'énergie interne d'une mole d'un gaz parfait monoatomique vaut U = 1,5RT. ( pour une mole d'un gaz diatomique U = 2,5 RT ) D'où CV m = dU/dT = 1,5 R ( gaz monoatomique) et CV m = dU/dT = 2,5 R ( gaz diatomique) Pour une mole de gaz parfait : H= U+PV = U+ RT CP m = dH/dT = dU/dT +R ; CP m - CV m = R. Coefficient de Laplace du gaz : g =CP m /CV m ; g CV m- CV m = R ; CV m= R / (g-1). CP m = R+CV m =R+R/( g-1) ; CP m= g R / (g-1). La température extérieure étant restée très longtemps égale à T0, le fond (F) du cylindre est mis en contact avec une source (ou thermostat) à la température T1 ; on laisse le système atteindre l’équilibre. Le volume V occupé par le gaz subit une diminution relative de 5 % à partir de la valeur initiale V0. En déduire la température Celsius finale si q0 = 27 °C. La pression est constante. Pf = Pi ; Pi Vi = RTi ; Pf Vf = RTf ; Vi -Vf =R / Pi (Ti -Tf ) R / Pi = Vi / Ti d'où : (Vi -Vf ) /Vi = (Ti -Tf ) / Ti = 0,05 Ti -Tf = 0,05 Ti ; Tf =0,95 Ti = 0,95(273,15+27) = 285 K ou ( 12°C). En fonction des températures et des données, exprimer la variation d’enthalpie du système lors de la transformation décrite ci-dessus, sous la forme DH = C'DT. Quelles propriétés essentielles de l’enthalpie utilise-t-on pour établir cette expression ? L'enthalpie est une grandeur extensive : DH = DH(gaz) + DH (cuivre). L'enthalpie est une fonction d'état, elle ne dépend que des température initiale et finale : DH =(n CPM(gaz) + mc) DT. Or CP m= g R / (g-1) d'où DH =(n g R / (g-1) + mc) DT. C' = n g R / (g-1) + mc. En déduire l’expression du transfert thermique Q algébriquement reçu par le système à travers (F). Faire l’application numérique et interpréter son signe. Q = DH= C' DT avec C' >0 et DT <0 : le système cède de l'énergie au milieu extérieur. g = 1,4 ; R = 8,314 J K-1 mol-1 ; n= 1 mole ; Capacité thermique massique du cuivre : c = 385 J.kg–1.K–1 ; m = 269 g ; DT = -15 K. Q = ( 1,4*8,314/0,4 + 0,269*385) *(-15) =-1,99 ~ -2,0 kJ Exprimer et calculer la variation d’énergie interne DU du système. Pour une mole de gaz parfait : H= U+PV = U+ RT DH= DU+ RDT ; DU = DH - RDT = -1,99 103 - 8,314 *(-15) = -1,87 kJ. DU = W+Q ; W =DU -DH= -1,99 +1,87 = 0,12 kJ W>0, le système reçoit du travail ; les forces pressantes extérieures poussent le piston mobile. On rappelle des expressions usuelles de la fonction d’état entropie S : SGP(T, V) = n CV m ln(T) + nT ln V + Cste ; SGP(T, P) = n CP m ln(T) - nT ln P + Cste ; Pour une phsase condensée de capacité C : Sphase condensée (T) = C ln(T) + Cste.   En fonction des températures et de C’, exprimer l’entropie créée lors de la transformation. Faire l’application numérique et conclure. Une mole de gaz parfait à pression constante : SGP(T0) = CP m ln(T0) + Cste ; SGP(T) = CP m ln(T) + Cste ; DSGP= CP m ln(T/T0). cuivre : SCu (T) = C ln(T) + Cste ; SCu (T0) = C ln(T0) + Cste ; DSCu= C ln(T/T0) L'entropie est une grandeur extensive : DS= DSCu+DSGP. DS=C ln(T/T0) + CP m ln(T/T0) = C' ln(T/T0) = 132,66 ln (285/300)= -6,80 J K-1. Entropie échangée : Séchange = Q / T1 =-1,99 103 / 285 = -6,98 J K-1. DS= Séchange + Scrée ; Scrée =DS- Séchange =-6,80 +6,98 = +0,18 J K-1. Scrée >0 : le transfert thermique est donc irréversible. Calorimètre à basse température. Sous pression atmosphérique, la température d’équilibre liquide-gaz du diazote est Te = 77,4 K. Il est commode de conserver l’azote liquide dans un « vase de Dewar », c’est-à-dire un récipient bien isolé thermiquement (mais non parfaitement) et communiquant avec l’atmosphère : le faible apport d’énergie à travers le vase entretient une lente ébullition du liquide qui s’évapore lentement. On dispose ainsi d’une « source de froid » commode et économique. Afin de mesurer la chaleur latente Lv de vaporisation de l’azote sous pression constante, on place sur une balance électronique un vase Dewar ouvert contenant de l’azote liquide : la diminution de la masse mesurée M au cours du temps traduit l’évaporation de l’azote. Le mode opératoire est le suivant : phase (1) : entre t = 0 et t = t1, on alimente une résistance R plongée dans le calorimètre : tension U et intensité I constantes ; phase (2) : le chauffage est coupé à t1 = 10 minutes. La masse M mesurée en grammes est enregistrée à intervalles réguliers de t = 0 à t2 = 15 minutes (figure ci-contre : t en secondes) ; on précise qu’à tout instant il reste de l’azote liquide dans le récipient. Comment évolue la température du liquide supposé homogène (justifier) ? La vapeur de diazote est en équilibre avec le liquide : la pression est constante ; appliquons la règle des phases : v = c+2-j. 1 constituant, le diazote et une relation N2(liq) = N2 (g) soit c=0 ; 2 phases liquide et gaz : j = 2. La variance est nulle; la pression étant fixée, la température reste constante soit 77,4 K. Pourquoi la masse diminue-t-elle même en l’absence de chauffage ? Pourquoi est-il difficile de l’empêcher ? L'écart de température entre l'intérieur du vase et l'extérieur est grand : il y a transfert thermique de l'extérieur vers l'intérieur du vase. Une partie du liquide s'évapore. 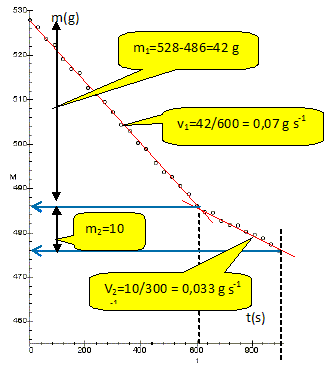Pour chaque phase de l’expérience, estimer la masse d’azote évaporé (m1 et m2). Calculer le rapport noté r des vitesses d’évaporation (phase1 / phase2). Voir graphe ci-dessus : r = 0,07 / 0,033 ~ 2,1. On désigne par PJ la puissance apportée par effet Joule et par P celle des autres transferts thermiques, puissances algébriquement reçues par l’azote et supposées constantes. Établir pour chaque phase de l’expérience une relation entre m1, m2, Lv, PJ, P et les dates nécessaires. Phase 1 : puissances reçues par le diazote : PJ+ P ; cette puissance reçue permet l'évaporation du diazote pendant 600 s : m1Lv/600. PJ+ P = m1Lv/600. (1) Phase 2 : puissance reçues par le diazote : P ; cette puissance reçue permet l'évaporation du diazote pendant 300 s : m2Lv/300. P = m2Lv/300. (2) En déduire une expression littérale de Lv indépendante de P, puis calculer sa valeur numérique si U = 8,5 V et R = 10 ohms. PJ = RI2 = U2/R ; (1) -(2) donne : U2/R = (m1-2m2) Lv/600 ; Lv = 600 U2/ ( R(m1-2m2)). Lv = 600*8,52 /(10*(42-20)) = 197 ~ 200 J g-1.

retour -menu