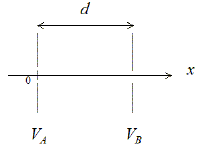spectrographe de masse par accélérateur, problème de chocs concours général 2009.

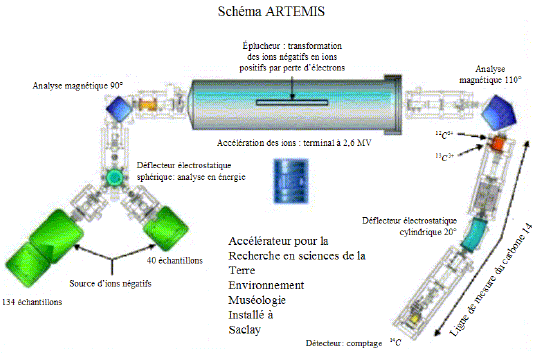
Comptage du 14C par SMA (spectrométrie de masse par accélérateur). La technique de spectrométrie de masse par accélérateur pour la datation radiocarbone consiste à compter séparément les atomes de 12C et les atomes de 14C restant dans un échantillon que l’on veut dater. La spectrométrie de masse conventionnelle permet depuis longtemps de discriminer les isotopes d’un même atome en fonction de leur masse et de les compter dans des temps relativement courts. Cependant, la proportion de 14C à mesurer est si faible qu’aucun détecteur ne s’est avéré suffisamment sensible. Dans les années 80, le couplage d’un accélérateur de particules à un spectromètre a permis de résoudre ce problème de détection. La très grande énergie conférée par l’accélérateur aux ions extraits de l’échantillon permet d’utiliser les détecteurs de particules ultra sensibles de la physique nucléaire. On élimine également, de cette façon, les atomes de même masse que le 14C qui par leur plus forte abondance gênent classiquement les mesures. Les échantillons à dater sont généralement transformés en graphite puis disposés dans la source de l’appareil où ils sont bombardés par des ions césium afin de produire un faisceau d’ions négatifs constitué de 12C- , 13C- ,14C- ,12CH2- , 13CH- , etc … Une première étape consiste à utiliser un premier aimant qui effectue alors une sélection des ions de masse 14. Ce faisceau, porté à très haute énergie grâce à la tension de plusieurs millions de volts régnant dans l’accélérateur, entre en collision avec des molécules gazeuses présentes au centre de lamachine ; les ions complexes comme 13CH- ou 12CH2- sont cassés puis épluchés de quelques électrons. Après avoir subi une nouvelle accélération dans la seconde partie de l’accélérateur, le faisceau constitué majoritairement d’ions 12C3+ , 13C3+ et 14C3+ est guidé vers un dispositif électromagnétique permettant une séparation fine des trois isotopes. Les ions 12C3+ et 13C3+ sont comptés par des instruments appelés cage de Faraday alors que les ions 14C3+ pénètrent dans un détecteur plus élaboré qui en mesurant leur énergie et leur perte de vitesse réalise un véritable comptage des ions 14C3+ . La technique SMA a l’avantage d’utiliser des échantillons d’une masse environ 1000 fois inférieure à celle nécessaire pour le comptage bêta, soit environ 1 mg et d’utiliser des temps très courts (environ 30 min). Ceci permet un plus grand choix des échantillons représentatifs de l’élément à dater et plus de statistiques en utilisant des matériaux différents. La possibilité de multiplier les analyses permet d’établir une chronologie détaillée. Expliquer pourquoi après la première étape (accélération et utilisation du premier aimant) les différents ions en sortie 14C- ,12CH2- , 13CH- ne peuvent donc pas être séparés par le spectromètre de masse. Ces ions ont la même masse et la même charge, c'est à dire le même rapport masse / charge ( m/e). Par spectrométrie de masse, seuls les ions dont le rapport m/e est différent peuvent être séparés. La force permettant la déviation des particules chargées est la force de Lorentz. Lors de la dernière étape de séparation des isotopes 12C- , 13C- ,14C-, quelle doit être l'orientation du champ magnétique B pour que les particules soient deviées et orientées vers les collecteurs ? Faire un schéma des vecteurs concernés. 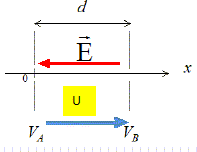Après l’étape de bombardement par les ions césium, l’échantillon est constitué d’un faisceau d’ions négatifs monochargés (14C- ,12CH2- , 13CH- ) que l’on va accélérer. Pour cela, ces ions vont pénétrer avec une vitesse initiale quasi nulle, dans une zone où règne un champ électrostatique constant créé à l’aide de deux électrodes soumises à une différence de potentiel : U=VA -VB telle que : E = |U| / d = constante. 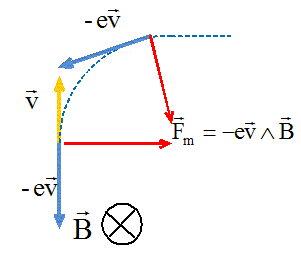Les vecteurs sont écrits en bleu et en gras. Quelle doit être l’orientation vectorielle du champ E pour que les ions soient accélérés ? Le travail W de la force électrique Fél = -eE doit être moteur. W = -eU, W >0 donc U est négatif. Déterminer la vitesse v acquise par les ions lorsqu’ils sortent de l’accélérateur. Calculer la valeur de cette vitesse pour 14C- . On prendra U=10 MV. NA = 6,022 1023 mol-1 ; M(146C) =14,003241 g/mol ; e = 1,60217733 10-19 C Le poids des ions est négligeable devant la force électrique. Wélect = e|U| Ecrire le théorème de l'énergie cinétique : ½mv2-0 = e|U| ; v = [2e|U| / m]½. m = M(146C) / NA =14,003241 10-3 / 6,022 1023 = 2,32535 10-26 kg v = [2*1,60217733 10-19 * 107 / 2,32535 10-26 ]½= 1,174 107 m/s. La vitesse dépend-t-elle des dimensions de l’accélérateur ? La vitesse dépend d de la charge, de la masse de l'ion ainsi que de la tension accélératrice. Elle ne dépend pas des dimensions de l'accélérateur. Sur quel(s) paramètres(s) agira-t-on pour moduler la vitesse des particules en sortie de l’accélérateur ? Pour des particules de même rapport e/m, en modifiant la tension accélératrice, on modifiera leur vitesse. La vitesse est proportionnelle à |U|½. A la sortie de cet accélérateur ( x > d ), quelle est la nature de la trajectoire de la particule ? (on considérera l’effet du poids négligeable). En absence de champ électrique ou magnétique, les ions ne sont soumis à aucune force. Le principe d'inertie indique que les ions sont animés d'un mouvement rectiligne uniforme. Concernant la dernière étape, les ions 14C3+ sont comptabilisés dans le détecteur. Pour cela, on évalue la perte de vitesse de ces ions lorsqu'ils penètrent dans un milieu. 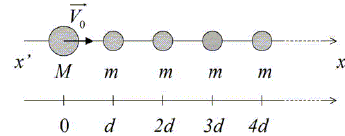Considerons le modèle suivant : un ion 14C3+ de masse M se déplace sur un axe xOx' et vient percuter un ensemble de particules de masses m, toutes séparées d'une distance d. Aucune autre interaction n'intervient. Les vecteurs sont écrits en bleu et en gras. L’élément de masse M possède une vitesse initiale V0 et les particules de masses m sont immobiles. Lors d’un choc entre particules, on parle de choc élastique (ce que nous supposerons ici) lorsqu’il y a conservation : - de la quantité de mouvement vectorielle totale (la quantité de mouvement d’une particule est le produit de la masse par le vecteur vitesse : p = m v - de l’énergie cinétique totale. Ainsi lors du choc élastique entre la particule de masse M et la première particule de masse m, on écrira : p0 + p'0 =p1 + p'1 et Ec M0 + Ec m0 = Ec M1 + Ec m1. p0 = MV0 et p1 = MV1 sont respectivement les quantités de mouvement de la masse M avant et après le choc. p'0 = mV'0 et p'1 = mV'1 sont respectivement les quantités de mouvement de la masse m avant et après le choc. Ec M0 et Ec M1 sont les énergies cinétiques de M avant et après le choc. Ec m0 et Ec m1 sont les énergies cinétiques de m avant et après le choc. Déterminer les expressions des vitesses V1 et V'1 en fonction des masses et des vitesses initiales. m est initialement immobile : p'0 = 0 et MV0 =MV1 + mV'1 ; V0 =V1 + m/MV'1 Les vitesses sont colinéaires portées par l'axe x'Ox. V0 et V'1 ont le sens de l'axe ; V1 peut avoir le sens de l'axe ( hypothèse n°1) ou le sens contraire si rebond ( hypothèse n°2) hypothèse n°1 : V0 = V1 + V'1 ; (1) ; hypothèse n°2 : V0 = -V1 + V'1 ; (2) ; Ec M0 = ½MV20 ; Ec m0 = 0 ; Ec M1 = ½MV21 ; Ec m1 = ½mV '21 ; Conservation de l'énergie cinétique : MV20 = MV21 +mV '21 ; V20 = V21 +m/MV '21 (3) ; on pose m/M = ß. (1) et (2) donnent : V21 = (V0 -V'1 )2 ; repport dans (3) : V20 =(V0 -V'1 )2 +ßV '21. V20 =V20 +V '21 -2V0V'1+ßV '21 ; 0 = V'1 [( 1+ß)V'1 -2V0] ; V'1 =2V0/( 1+ß). (4) (3) et (4) conduisent à : V21 = V20 -4ßV20 /(1+ß)2 ; V1 = + ou - (1-ß)/(1+ß)V0. Discuter les signes de ces vitesses pour M < m et M > m . Commenter le mouvement des particules dans chaque cas ? M < m : ß >1 ; V1 < 0 ; V1 a le sens contraire de l'axe (rebond). M > m : ß <1 ; V1 < 0; V1 a le sens de l'axe. Que se passe-t-il pour le cas particulier ou M = m ? ß =1, V1 =0, la particule " projectile" reste immobile après le choc. V'1 = V0 , la cible, initialement immobile, possède la vitesse V0 après le choc. Peut-on avoir V1 >V0 ? Justifier sans calcul. V20 = V21 +m/MV '21 (3) m/M est positif, V1 ne peut être supérieur à V0. Quelle est la nature du mouvement de la particule de masse m jusqu' à la collision suivante avec sa plus proche voisine ? En absence de champ électrique ou magnétique, les ions ne sont soumis qu'à leur poids, perpendiculaire à la vitesse ( détecteur horizontal). Le poids ne travaille pas,; l'énergie cinétique n'est pas modifiée ; la valeur de la vitesse est constante : le mouvement est uniforme. On néglige la taille des particules et l’on considère que le premier choc a lieu pour x = d. Donner les abscisses xn des collisions successives de la particule de masse M. La particule n°1 de masse m heurte la particule n°2 de masse m, à la vitesse V'1. La particule n°1 s'arrête et la particule n°2 part avec la vitesse V'1. La particule n°2 de masse m heurte la particule n°3 de masse m, à la vitesse V'1. La particule n°2 s'arrête et la particule n°3 part avec la vitesse V'1. Et ainsi de suite. Donc xn = nd. En utilisant les résultats précédents, exprimer la vitesse Vn+1 de la particule de masse M en fonction de la vitesse Vn. Vn+1 = (1-ß)/(1+ß)Vn avec ß= m/M et m< M. En déduire une expression de la vitesseVn en fonction de V0. V1 = (1-ß)/(1+ß)V0 ; V2 = (1-ß)/(1+ß)V1 =[ (1-ß)/(1+ß)]2V0. Vn =[ (1-ß)/(1+ß)]nV0. En posant x = nd , établir une loi continue équivalente donnant la vitesse V(x) de la particuleen fonction de la position. n = x/d d'où V(x) =[ (1-ß)/(1+ß)]x/d V0. Peut on définir une distance d’arrêt pour la particule incidente ? (1-ß)/(1+ß) est un nombre inférieur à 1 ; [(1-ß)/(1+ß)]x/d va tendre vers zéro si x devient très grand. On peut donc définir une distance d'arrêt. Nous sommes à présent face à un paradoxe : pour répondre aux questions précédentes, nous avons utilisé les lois de conservation lors d’un choc élastique, en particulier la conservation de l’énergie cinétique et pourtant nous prétendons voir s’arrêter la particule incidente : comment résoudre cette contradiction ? Avancer une piste de réflexion. L'énergie cinétique de la particule incidente est transmise aux particules cibles de masse m, qui sont tour à tour mise en mouvement.

c

retour -menu