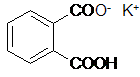|
Dosage acide base, suivi cinétique, conductimétrie chimie concours DGCCRF 08 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
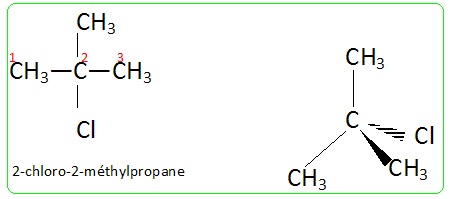
On considère l'hydrolyse du chlorure de tertiobutyle : CCl(CH3)3 (aq) + H2O(l) = HOC(CH3)3 + H+(aq) + Cl-(aq) (1) Quel est le nom du chlorure de tertiobutyle en nomenclature officielle ? Le représenter en utilisant la représentation de Cram.
La réaction produit de l'acide chlorhydrique et un alcool : quel est son nom ? 2-méthylpropan-2-ol De quel type de réaction s'agit-il ? Substitution nucléophile.
Une solution de soude à environ 1 mmol.L-1 étant difficile à préparer directement, on prépare une solution à 0,1 mol.L-1, que l'on diluera ensuite 100 fois afin d'effectuer les dosages. La soude de concentration environ égale à 0,1 mol.L-1 est étalonnée par pesée d'hydrogénophtalate de potassium, de formule :
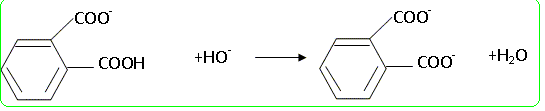
On pèse une masse m = 0,3051 g d'hydrogénophtalate de potassium que l'on dissout dans environ 50 mL d'eau. Un dosage avec la soude suivi par colorimétrie donne un volume équivalent Veq = 12,45 mL. Ecrire l'équation de la réaction ayant lieu lors de l'étalonnage.
Exprimer et calculer la concentration exacte de la soude [précision 0,8%]. Hydrogénophtalate de potassium (C8H5KO4) : M = 204,23 g.mol-1, pKA1 = 2,9, pKA2 = 5,1. Quantité de matière hydrogénophtalate de potassium : n = m/M = 0,3051 / 204,23 =1,494 10-3 mol A l'équivalence : n = CB VE ; CB = n / VE = 1,494 10-3 / 12,45 10-3 =1,20 10-1 mol/L. Calculer le pH de la solution à l'équivalence. En déduire un indicateur coloré possible pour le dosage. La réaction prépondérante est : -OOC-C6H4-COO- + H2O = -OOC-C6H4-COOH +HO-. K = [HO-][-OOC-C6H4-COOH] / [-OOC-C6H4-COO-] = [HO-][H3O+][-OOC-C6H4-COOH] /( [-OOC-C6H4-COO-][H3O+]) K = 10-14/ 10-pKa2 = 10-14/ 10-5,1 =1,26 10-9, valeur faible, la réaction est très limitée. [-OOC-C6H4-COO-]éq ~ 0,12 mol/L ; La solution reste électriquement neutre : [-OOC-C6H4-COOH]éq = [HO-]éq ; K = [HO-]éq2 / 0,12 [HO-]éq= (K*0,12)½ = ( 1,26 10-9 * 0,12)½ =1,2 10-5 mol/L ; [H3O+]éq=10-14/1,2 10-5 = 8,1 10-10 mol/L ; pHéq = 9,0. La zone de virage de l'indicateur coloré doit contenir la valeur du pH à l'équivalence : la phénolphtaléine convient. Quel volume doit-on prélever de cette solution pour préparer 500 mL de solution diluée 100 fois ? Donner la concentration de la solution ainsi obtenue. On prélève 500 / 100 = 5,00 mL de la solution mère. La concentration de la solution fille est : 1,20 10-1 /100 = 1,20 10-3 mol/L. Pourquoi doit-on préparer cette solution de soude au dernier moment? Ecrire la ou les équation(s) bilan correspondant aux réactions parasites pouvant se produire. La dissolution du gaz carbonique de l'air est suivie de la réaction : CO2(aq) + HO- = HCO3- avec K= [HCO3- ] / ([CO2(aq)][HO- ])= [HCO3- ][H3O+] / ([CO2(aq)][HO- ][H3O+])= 10-6,3 / 10-14 =107,7. cette réaction est totale. La réaction suivante se produit alors : HCO3- + HO- = CO32- +H2O avec K= [CO32- ] / ([HCO3-][HO- ])= [CO32- ][H3O+] / ([HCO3-][HO- ][H3O+])= 10-10,3 / 10-14 =103,7. cette réaction est totale, sauf si la solution de soude a dissout une quantité importante de CO2.
Dans le tableau suivant, on a reporté les volumes équivalents en solution d'hydroxyde de sodium trouvés lors des dosages des prises d'essai du milieu réactionnel :
Trempe ou blocage cinétique : la composition du mélange ne varie pratiquement pas à basse température, ce qui nous laisse le temps de faire le dosage de l'acide chlorhydrique formé. Exprimer la loi de vitesse associée à la réaction (1) sachant que l'ordre partiel par rapport à l'eau est égal à 0. Les notions de loi de vitesse et d'ordre partiel sont expliquées en début d'énoncé. CCl(CH3)3 (aq) + H2O(l) = HOC(CH3)3 + H+(aq) + Cl-(aq) (1) v = k [CCl(CH3)3]p. En déduire l'unité de la constante k en fonction de p. v : mol.L-1.[temps]-1 ; [CCl(CH3)3]p : mol p L-p ; k : mol1-p.L-1+p.[temps]-1. Calculer la concentration initiale en chlorure de tertiobutyle. C(CH3)3Cl : M = 92,57 g.mol-1 ; d = 0,850. "On introduit ensuite dans cet erlenmeyer 100 µL de ClC(CH3)3 ..." 100µL = 0,1 mL ; masse m = 0,100 * d = 0,100*0,850 = 0,0850 g n = m/M = 0,0850 / 92,57 = 9,18 10-4 mol dans 50 mL ( 0,050 L). [ClC(CH3)3]0 = 9,18 10-4 / 0,050 = 1,84 10-2 mol L-1. Après avoir donné l'équation du dosage, exprimer la concentration en acide chlorhydrique en fonction du volume de soude versé à l'instant t donné. En déduire la concentration en chlorure de tertiobutyle en fonction de ce volume. " On prélève alors à intervalles de temps réguliers un volume V = 5,00 mL du milieu réactionnel que l'on verse dans un bécher contenant environ 20 mL d'eau glacée" HO- + H3O+ = 2H2O. A l'équivalence CaV = CbVéq ; Ca= CbVéq/V= 1,20 10-3 / 5,00 Véq = 2,40 10-4 Véq avec Véq en mL. [ClC(CH3)3]t = [ClC(CH3)3]0 - 2,40 10-4 Véq.
[ClC(CH3)3]t = [ClC(CH3)3]0 - 2,40 10-4 *36,65 =1,84 10-2 -8,80 10-3 = 9,6 10-3 mol/L ( réaction non terminée) Qu'appelle-t-on temps de demi-réaction ? Donner ici une valeur approximative. Durée au bout de laquelle l'avancement est égal à la moitié de l'avancement final. Dans l'hypothèse d'une réaction totale, l'avancement final vaut : [ClC(CH3)3]0 * 0,05 = 1,84 10-2 * 0,05 =9,2 10-4 mol. A t½, l'avancement vaut 0,5*9,2 10-4 = 4,6 10-4 mol soit Ca V= 4,6 10-4 mol dans 50 mL ou 4,6 10-5 mol dans 5 mL. Par suite CbVéq = 4,6 10-5 et Véq =4,6 10-5 / 1,20 10-3 = 3,8 10-2 L = 38 mL. Le temps de demi réaction ( d'après le tableau ci-dessus) est voisin de une heure.
Le suivi cinétique de cette réaction peut se faire de manière plus simple et plus rapide par conductimétrie ou directement par suivi pH-métrique. Expliquer le principe d'un conductimètre. La conductance d’une solution est proportionnelle aux concentrations des ions ( aux faibles concentrations). La conductimétrie, mesure de la conductance ou de la conductivité, permet de déterminer des concentrations. Le suivi de cette réaction peut se faire par cette méthode cinétique car parmi les produits apparaissent deux ions ; ces derniers contribuent à la conductivité de la solution. il est nécessaire d'étalonner le conductimètre : réglage de la température ( la conductivité dépend de la température) et connaitre la constante de cellule ou caractéristiques de la sonde de mesure donnée par le constructeur. Le fabricant de conductimétres fournit une table de la conductivité d’une solution de chlorure de potassium à 0,1 mol/L pour toutes les températures allant de 15,0 et 30,0°C. Mesurer la conductance de cette solution de chlorure de potassium et la température de la solution ; cette table permet de déterminer la constante de la cellule utilisée. Un potentiométre d’étalonnage permet d’ajuster la valeur lue. Donner l'allure de la courbe obtenue en traçant s= f(t). s = lH3O+ [H3O+] + lCl- [Cl-] ; or [H3O+] = [Cl-] d'où : s = (lH3O+ + lCl- ) [H3O+] Dans l'hypothèse p = 0 : [A]=[A]0 -kt ; [H3O+] = [A]0 - [A] = kt ; droite Dans l'hypothèse p = 1 : [A]=[A]0 exp(-kt) ; [H3O+] = [A]0 - [A] = [A]0 ( 1-exp(-kt)) La courbe croît de manière exponentielle au début puis tend vers une limite [H3O+] = [A]0. Donner l'allure de la courbe obtenue en traçant pH = f(t). Pourquoi n'a-t-on pas choisi cette dernière méthode ? Dans l'hypothèse p = 0 : [A]=[A]0 -kt ; [H3O+] = [A]0 - [A] = kt ; pH = -log k - log t La courbe pH = f(t) n'est pas une droite. Dans l'hypothèse p = 1 : [A]=[A]0 exp(-kt) ; [H3O+] = [A]0 - [A] = [A]0 ( 1-exp(-kt)) pH = -log [A]0 -log ( 1-exp(-kt)) Le suivi cinétique d'une réaction de type SN2 donne une loi de vitesse faisant apparaître un ordre partiel égal à 1 pour chacun des deux réactifs. Exprimer la vitesse de réaction. v = k [A][B].
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|