Radioactivité, dipôles (RC) , (RL) et (RLC) concours Fesic 2009

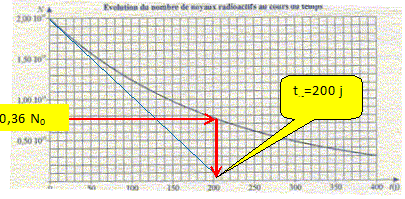
Le potassium 40 4019K est radioactif et se désintègre en donnant de l'argon 4018Ar. La demi-vie radioactive de 4019K est 1,5 109 ans. A- Il s'agit d'une désintégration ß+. Vrai. 4019K ---> 4018Ar +01e. L'analyse d'un caillou lunaire montre la présence de potassium 40 et d'argon 40. On suppose que l'argon 40 provient uniquement de la désintégration du potassium 40. A la date t, on relève : NK(t) = 1,0 1016 noyaux et NAr(t) = 3,0 1016 noyaux. B- 2,0 1016 noyaux de potassium 40 se sont désintégrés. Faux. La désintégration de 2,0 1016 noyaux de potassium 40 conduit à la formation de 2,0 1016 noyaux d'argon 40. C-Le nombre de noyaux initiaux de potassium 40 est 4,0 1016. Vrai. La désintégration de 3,0 1016 noyaux de potassium 40 conduit à la formation de 3,0 1016 noyaux d'argon 40. Et il reste encore 1,0 1016 noyaux de potassium 40 : initialement il y avait 4 1016 noyaux de potassium 40. D- L'âge de ce caillou est 3,0 109 ans. Vrai. Au bout d'une demi-vie il reste 2 1016 noyaux de potassium 40. Au bout de 2 demi-vie il reste 1 1016 noyaux de potassium 40. 2 demi-vie correspondent à 2* 1,5 109 ans. le noyau de l'atome de polonium 210 21084Po se désintègre suivant : 21084Po--->20682Pb + 42He A- c'est une désintégration ß-. Faux. ( radioactivté alpha) On mesure le nombre N de noyaux de polonium 210 présents dans un échantillon. L'évolution de N en fonction du temps est donnée :     B- L'expression mathématique de la variation de N en fonction du temps t s'écrit N = N0/t. Faux. N (t) = N0 exp(-lt) ; dN/dt = -lN0 exp(-lt) = - lN C-La constante de temps radioactive du polonium 210 est T = 270 j. Faux. to = 200 j ; l = ln2 / t½ et la constante de temps vaut 1/l =to ; l =1/t0 = 1/200 =0,005 j-1 ; t½ = ln2 / l =200 ln 2 ~ 140 j. D- On peut à l'aide de cette courbe, prévoir au bout de combien de temps un noyau donné de polonium 210 va se désintégrer. Faux. 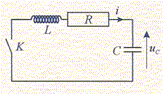Soit un dipole (LC )dans lequel la tension aux bornes du condensateur peut s'écrire en fonction du temps : u(t) = Um cos ( 2 pi t/T0) avec Um = 4,0 V. le condensateur a une capacité C = 2,2 mF et l'inductance de la bobine est L = 0,50 H. A- Lorsque toute l'énergie est stockée dans le condensateur, la charge électrique portée par l'une de ses armatures est 8,8 mC. Vrai. qm=CUm = 2,2 *4,0 = 8,8 mC B- L'exppression du courant électrique circulant dans le circuit est donnée par : i(t) =-C( 2 pi /T0)cos ( 2 pi t/T0). Faux. q(t) = Cu(t) = CUm cos ( 2 pi t/T0) i(t) = dq(t)/dt = CUm (-1) ( 2 pi /T0)sin ( 2 pi t/T0) C-L'énergie stockée dans le condensateur est maximale lorsque le courant électrique est nul . Vrai. si i(t) = 0 : Em =½Li2 = 0 ; Eélec = ½CUm2. D- A la date t= 0,25 T0 toute l'énergie est stockée dans la bobine. Vrai. 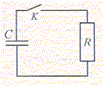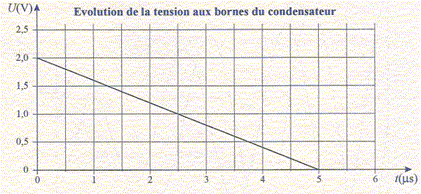i(0,25 T0) = CUm (-1) ( 2 pi /T0)sin ( 0,5 pi ) = CUm (-1) ( 2 pi /T0) u(0,25 T0) = Um cos ( 0,5 pi) = 0 R = 1,0 103 ohms ; C =2,2 mF ; E=5,0 V. Le condensateur étant préalablement déchargé, à la date t=0 on ferme l'interrupteur K. A-u(t) = E(1-exp(-t/t) est solution de l'équation différentielle E = RCdu/dt + u. Vrai. B- l'intensité est nulle à la date t=0. Faux. q(t) = Cu(t) = CE(1-exp(-t/t) i(t) = dq(t)/dt = CE / t exp(-t/t) ; i(t=0) = CE / t = CE/(RC) = E/R. C- La constante de temps du circuit de charge est 4,0 s. Faux. RC = 1,0 103 *2,2 10-3 = 2,2 s D- Au bout de 20 s, la charge qA est égale à 0,011 C . Vrai. 20 s est bien supérieure à 5 fois la constante de temps : la charge est terminée et qA = CE =2,2 10-3*5 = 1,1 10-2 C. 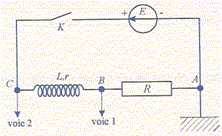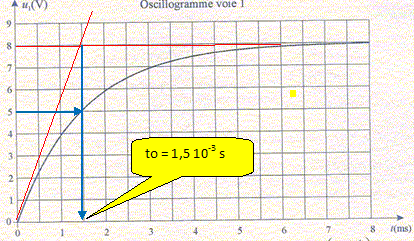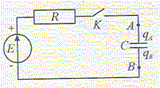E= 10,0 V ; R = 40 ohms A- La voie 1 visualise la tension aux bornes du résistor. Vrai. Voie 1, on visualise UBA= R i. Quand l'interrupteur K est fermé depuis longtemps l'intensité I est constante et vaut 0,20 A. B- La résistance de la bobine vaut r = 10 ohms. Vrai. UCB = LdI/dt + rI avec dI/dt = 0 ; E =UCB +UBA= rI + RI r = E-I-R = 10,0/0,20 -40 = 10 ohms. C- L'expression de la tension visualisée sur la voie 1 est de la forme : u1(t) = u0(1-exp(-t/to). Vrai. D- La détermination de la constante de temps to permet de calculer la valeur de l'inductance L~ 75 mH. Vrai. to = L/(R+r) ; L = (R+r) to = 50 *1,5 10-3 = 7,5 10-2 H = 75 mH. Un condensateur de capacité C = 50 µF a une tension entre ses bornes U=2,0 V. A- L'énergie emmagasinnée dans ce condensateur est 1,0 10-4 J. Vrai. ½CU2 = 0,5*50 10-6 * 4 = 1,0 10-4 J. B- La charge portée par l'armature positive du condensateur est q = 25 µC. Faux. q = CU = 50*2,0 = 100 µC Le condensateur est monté en série avec un résistor de résistance R= 10 ohms et un interrupteur K : C- La constante de temps du circuit est to = 5 µs. Faux. to = RC = 10*50 = 500 µs. A la date t=0, on ferme l'interrupteur. D- L'évolution de la tension aux bornes du condensateur est la suivante. Faux. 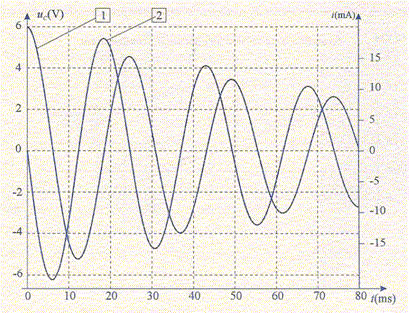C = 16 µF. Avant la fermeture de l'interrupteur l'intensité est nulle. A t=0, on ferme l'interrupteur et on démarre l'enregistrement. On pourra considéré que l'amortissement du circuit est faible. On donne 64 pi2 ~ 252. A- La courbe 2 correspond à l'intensité du courant dans le circuit. Vrai. Continuité de l'intensité dans la bobine : i(t=0-) = i(t=0+)=0. B- Le circuit possède une énergie initiale E0 = 0,29 mJ. Vrai. Le condensateur stocke initialement l'énergie du circuit : E0 = ½C Uc2 avec Uc(0) = 6 V ( lecture courbe 1) E0 = 0,5* 16 10-6 * 62 = 2,9 10-4 J = 0,29 mJ C- L'intensité est en avance sur la tension d'une demi-période. Faux. L'intensité est en avance sur la tension d'un quart de période. D- La valeur de l'inductance de la bobine est L~ 0,1 H. Faux. courbe 2 : 2 période correspondent à environ 50 ms soit 0,05 s ; T ~0,025 s Or T = 2 pi (LC)½ ; L = T2/(4pi2C) =(25 10-3)2 / ( 4 pi2 *16 10-6) ~252 10-6 / (252 10-6) ~1 H.

retour -menu