Satellite, bille de flipper, pendule élastique : physique concours FESIC 08

Répondre par vrai ou faux. La terre est assimilée à une sphère homogène de masse M et de rayon R. Une navette spatiale a été placée sur une orbite circulaire à une altitude h = 260 km. A cette altitude, l’accélération de la pesanteur est d’environ 9 m.s-2. La durée d’une révolution de la navette autour de la terre est T. Données : pi .10 ½ ~ 10 ; 6640 ½ ~81 ; R= 6380 km.  A- La navette a un mouvement circulaire uniforme. Vrai. B- D’après la troisième loi de Kepler : T2 R3 = 4 pi2 GM Faux. A la place de R3 il faut écrire (R+h)3. C- La période de révolution de la navette est T = 5,4.103 s. Vrai. g = GM / (R+h)2 ; GM = g(R+h)2 par suite la 3ème loi de Kepler s'écrit : T2 (R+h)3 = 4 pi2 g(R+h)2 T2 R+h = 4 pi2 g T2 = 4 pi2(R+h) / g = 4*pi2 *(6380+260) 103 / 9 = 4*pi2 *6640 103 / 9 T = 2 pi 10½*81 *10/3 = 2*10*27*10 = 5400 s. D- La navette spatiale tourne sur son orbite avec une vitesse angulaire supérieure à celle d’un satellite géostationnaire. Vrai. fréquence f = 1/T = 1/5400 ; vitesse angulaire : 2 pi / 5400 rad/s. période d'un satellite géostationnaire : 24 h = 24*3600 = 86400 s vitesse angulaire : 2pi / 86400 rad/s. Un lanceur de flipper est constitué d’un ressort de constante de raideur k = 50 N.m-1 et de longueur à vide l0 = 12 cm. Il permet de propulser une bille d’acier, de masse m = 20 g, selon la ligne de plus grande pente d’un plan incliné faisant un angle a avec l’horizontale. 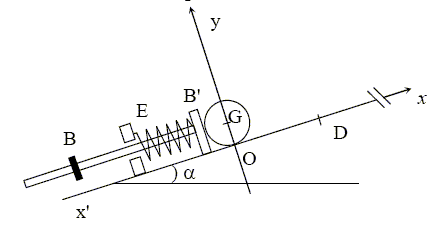Un joueur tire sur la tige et comprime ainsi le ressort, jusqu’à ce que le centre d’inertie de la bille se trouve immobile au niveau du point O. La longueur du ressort ainsi comprimé est égale à 8,0 cm. En lâchant la tige, il libère le dispositif qui propulse la bille. Lorsque le centre d’inertie de la bille arrive au niveau du point D, la butée B bloque le mouvement du ressort qui retrouve dans cette position sa longueur à vide et libère la bille. Remarques : La bille reste en contact avec le lanceur de O à D. Les forces de frottement peuvent être considérées comme négligeables par rapport aux autres forces. 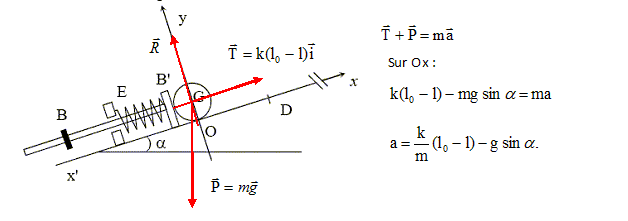A-Lors de la phase de lancement, la force exercée par le ressort sur la bille est supérieure à la force exercée par la bille sur le ressort. Faux. Principe des actions réciproques ( 3ème loi de Newton). Interaction entre un objet A et un objet B : si un solide noté A exerce sur un solide noté B une force notée F A / B, alors B exerce sur A une force notée F B / A . Les deux forces associées à une même interaction sont toujours égales et opposées. B- Lors de la phase de lancement, entre les positions O et D, le mouvement de la bille est uniformément accéléré. Faux. L'accélération n' a pas une valeur constante ( l0- l diminue) : le mouvement n'est pas uniformément accéléré. C- L’énergie potentielle élastique du ressort est égale à 40 mJ lorsqu’il est comprimé. Vrai. Energie potentielle élastique : ½k( l0-l)2 = 0,5*50(0,12-0,08)2 =25*(4 10-2)2 =25*16 10-4 = 400 10-4 = 40 10-3 =40 mJ. D- L’énergie cinétique acquise par la bille en D est égale à 40 mJ. Faux. On choisit l'origine des énergies potentielles en D. En O, l'énergie mécanique du système bille ressort est sous forme potentielle de pesanteur et potentielle élastique. EM = ½k( l0-l)2 - mg ( l0-l) sin a. En D, l'énergie mécanique du système bille ressort est sous forme cinétique. EM =½mv2. Conservation de l'énergie mécanique : ½k( l0-l)2 - mg ( l0-l) sin a = ½mv2. 0,04- mg ( l0-l) sin a = ½mv2. L'énergie cinétique est inférieure à 40 mJ en D ( il faut retrancher à 40 mJ, le travail du poids entre O et D ). Soit le pendule élastique ci-dessous constitué d’un cylindre de masse m = 200 g attachée à un ressort dont la constante de raideur est k = 20 N.m-1. 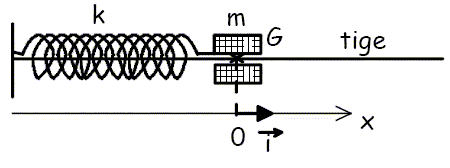On considère que l’ensemble peut coulisser sans frottements sur une tige horizontale. Lorsque le cylindre est en équilibre, son centre d’inertie coïncide avec la graduation O de l’axe. Données : 2 pi ~ 6,3 ; 10½ ~ 3,2 ; 6,3 *3,2 ~ 20. cos (-pi/4) = ½ 2½ ; tan(-pi/4) = -1 ; 2 / 2½~ 1,4. A- La période des oscillations de ce pendule est de 0,63 s. Vrai. T = 2 pi (m/k)½ = 2 pi ( 0,2/20)½ =2 pi ( 0,01)½ =2 pi *0,1 = 6,3*0,1 = 0,63 s. La solution générale de l’équation différentielle du mouvement s’écrit sous la forme : x(t) = xm cos ( 2 pi t / T0 + j0) où xm est l'amplitude (m), T0 la période (s) et j0 la phase à l'origine. On écarte le solide de sa position d’équilibre d’une distance x telle que x = +2,0 cm, puis on le lance avec une vitesse de composante v0x = +0,20 m.s-1. B- L’équation horaire du mouvement est : x(t) = 2,8.10-2cos( 10t - pi/4). Vrai. Pulsation : 2pi/T0 = 6,3 /0,63 = 10 rad/s. Amplitude xm : Le solide est lancé vers la droite avec une vitesse v0x = +0,20 m.s-1. Conservation de l'énergie mécanique : ½k x02 +½mv0x2 = ½kxm2. 0,5 *20 *(2 10-2)2 +0,5*0,2*0,22 = 0,5*20 xm2. 10*4 10-4 +0,1*0,04 = 10 xm2. 4 10-3 +4 10-3 =10 xm2 ; xm2 = 2*4 10-4 ; xm =1,4 *2 10-2 = 2,8 10-2 m. phase à l'origine : l'origine des dates est celle du lancé. x(0) =2 10-2 = 2,8 10-2 cos (j0 ) ; cos (j0 ) = 1/1,4 = 1/2½ ; j0 = + ou - pi/4. vitesse initiale : dériver x(t) par rapport au temps v(t) = -2,8 10-2 *10 sin (10t+j0) v(0) = +0,2 = -0,28 sin (j0) ; sin (j0) = -1/1,4 ; j0 = -pi/4. C- Le mobile inverse le sens de son mouvement à la date t1=pi/40 s. Vrai. à la date t1, x(t1)= + xm = xm cos(10 t1-pi/4). +1 = cos(10 t1-pi/4) ; 10 t1-pi/4 = 0 ; t1 = pi /40. D- Le mobile repasse par sa position d’équilibre à la date t2= 3pi/40 s. Vrai. à la date t2, x(t2)= 0 = xm cos(10 t2-pi/4). 10 t2-pi/4 = pi/2 ; t2 = 3 pi/40. autre solution : 10 t2-pi/4 = -pi/2 ; t2 = - pi/40. ( ne pas retenir, un temps doit être positif).

retour -menu