Ondes : physique concours ECE 08

Répondre par vrai ou faux. Un nageur A décide de sauter d’une hauteur h = 8 m dans une rivière. En-dessous de lui à la verticale, nage une autre personne B. Le plongeur prévient son camarade à la date t0 = 15 h 32 min 24 s qu’il saute maintenant en émettant un son de fréquence f = 400 Hz. La célérité du son est c = 340 m.s-1. A- La longueur d’onde du son émis par A est de 85 m. Faux. Longueur d'onde l = c/f =340/400 =0,85 m. B- La date d’arrivée du signal est t = 15 h 32 min 24,024 s. Vrai. Pour parcourir 8 m, le son met : 8/340 = 0,024 s Le nageur B prévenu, nage pour s’éloigner du point de chute du nageur A. Il nage à la vitesse constante de 1,5 m.s-1. Au moment où B commence à s’éloigner, A saute et arrive 1,5 s plus tard. A cet instant B arrête de nager. A crée une vague qui rattrape B au bout de 10 s. C- La vitesse de l’onde à la surface de l’eau est c1= 225 m/s. Faux. B parcourt une distance égale à : 1,5*1,5 = 2,25 m. célérité de l'onde à la surface de l'eau : 2,25/10 = 0,225 m/s. D- Cette onde déplacera le nageur B verticalement, mais pas horizontalement car la propagation de l’onde s’effectue sans transport de matière Vrai. Une personne, assise au bord d’une piscine, bat du pied, régulièrement dans l’eau à une fréquence de 4 Hz et crée ainsi une onde périodique à la surface de l’eau de hauteur maximale 0,15 m. Le déplacement des éléments du milieu peut être décrite par l’équation suivante : z(t) = a cos [2 pi/T0(t-x/c) +F], c vitesse de propagation de l’onde à la surface de l’eau est de 2 m/s. A- a est l’amplitude, T0 est la période propre et F est la phase à l’origine. Vrai. B- En prenant F =0, l’expression de la vitesse de déplacement vertical d’un point du milieu est : v(t) = -a 2 pi/T0 sin [2 pi/T0(t-x/c)]. Vrai. C- La hauteur de la vague à la date t = 8 s et à 8 mètres du pied est maximale. 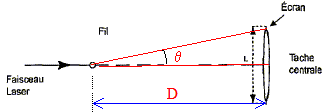Vrai. z(8) = a cos [2 pi/T0(8-8/2) +F]= a cos[8 pi /T0 +F] fréquence f = 4 Hz ; T0 = 1/4 = 0,25 s ; z(8) =a cos[8 pi /0,25 +F] = a cos[16 pi +F]. Si F = 0, z(8) = a. D- La vitesse du déplacement des éléments du milieu à la date t = 2 s et à 2 mètres du pied est nulle. Vrai. v(2) = -a 2 pi/T0 sin [2 pi/T0(2-2/2)] = -a 2 pi/T0 sin [2 pi/T0] =-a 2 pi/T0 sin [2 pi/0,25] =-a 2 pi/T0 sin [8 pi] =0. A-La fréquence de l’onde lumineuse émise par ce laser est 5,00 1014 Hz. Vrai. l = 600 nm = 600 10-9 m = 6,00 10-7 m ; f = c/l = 3,00 108 / 6,00 10-7 =5,00 1014 Hz. B- L’écart angulaire entre le milieu de la tache centrale et la première extinction est donné par la relation q = a/l. Faux. q = l/a avec : l longueur d'onde (m) et a : diamètre du fil ou largeur de la fente (m) C- La largeur de la tache centrale est de 1,2 cm. Faux. tan q = ½L/D voisin de q radian pour les angles petits. en tenant compte des deux relations ci-dessus : ½L/D=l/a soit L = 2l D/a. L = 2* 6,00 10-7*2,0 / 10-4 =2,4 10-2 m = 2,4 cm. D- Lorsque cette onde lumineuse se propage dans de l’eau (indice de réfraction 1,33), la fréquence de cette onde ne change pas. Vrai. On attache une masse de 200 g à l’extrémité B d'une corde maintenue horizontale sur sa plus grande longueur, puis on produit une déformation sinusoïdale, de fréquence 100 Hz, à l’extrémité A de la corde, grâce à un vibreur. 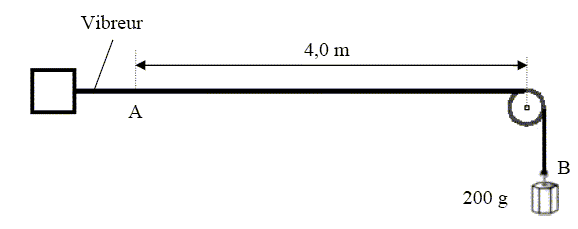La célérité des ondes le long de la corde est donnée par la relation : v = (T/m)½. T est la tension de la corde et m= 20 g m-1, la masse linéique de la corde. On prendra : g = 10 N.kg-1 et on admettra que la valeur de la tension de la corde est égale au poids de la masse suspendue. A- La tension peut s’exprimer en kg.m.s-1. Faux. force = masse * accélération = masse *longueur / temps2 ; [tension] =M L T-2. B- La célérité de l’onde augmente avec la masse linéique de la corde. Faux. v = (T/m)½ ; la célérité diminue si la masse linéique augmente. C- La corde est le siège d’oscillations forcées. Vrai. Une corde tendue entre deux points fixes et soumise à une excitation sinusoïdale entre en résonance lorsque les fréquences excitatrices sont multiples d'une même fréquence f0, appelé mode fondamental. On peut observer la formation d'ondes stationaires. D- La valeur de la longueur d’onde est l =10 cm. Vrai. T = mg = 0,2*10 = 2 N ; m = 20 g m-1 = 0,020 kg m-1 ; v = [2/0,02]½ =10 m/s. f = 100 Hz ; l =v /f = 10 / 100 = 0,10 m = 10 cm. A- La vitesse de propagation d'une onde mécanique est proportionnelle à l'amplitude de la perturbation. Faux. Soit une onde lumineuse de fréquence f et de longueur d'onde l. B- La relation qui lie ces deux grandeurs est f = l/ c . Faux. f = c/l. Un faisceau de lumière monochromatique, de longueur d'onde l, arrive sur une fente verticale d’une largeur a de l’ordre du mm. C- On observe alors sur l'écran, situé à une distance D une figure de diffraction verticale. Faux. La largeur de la fente n'est pas du même ordre de grandeur que la longueur d'onde : la diffraction sera peu marquée. La figure de diffraction sera horizontale, la fente étant verticale. D- La tache centrale de diffraction possède une largeur L égale à 2 lD/a. Vrai. Une corde horizontale, supposée infinie, est soumise à un ébranlement transversal sinusoïdal à partir de son extrémité O. L’origine des temps est prise lorsque O passe par sa position d’équilibre en allant vers le haut. Sa fréquence est de 100 Hz et son amplitude de 1 mm . Il se propage dans le sens positif, de la gauche vers la droite, avec une célérité de 5 m.s-1 . Les amplitudes y sont exprimées en mm. A- L’équation horaire du point O est y (t ) = sin(200 pi t). Vrai. pulsation w = 2 pi * fréquence = 2 pi*100 = 200 pi rad/s : amplitude = 1 mm. B- L’équation horaire du point N1 situé 5 cm à droite de O est y (t ) = sin(200 pi t). Vrai. longueur d'onde l = c/f = 5/100 = 0,05 m = 5 cm. O et N1, distants d'un nombre entier de longueur d'onde sont en phase. C- L’équation horaire du point N2 situé 2,5 cm à droite de O est y (t ) = -sin(200 pi t). Vrai. O et N2, distants d'un nombre impair de demi-longueur d'onde sont en opposition de phase. D- A l’instant t = 0 , la corde est représentée par la courbe y(x) = sin (40 pi x) . Faux. y(t, x) =sin[ 2pi f(t-x/c)] =sin[ 200 pi(t-x/5)] y(0, x) =sin (-200 pi x/5) = -sin (40 pi x) E- A l’instant t = 5 ms , la corde est représentée par la courbe y(x) = - sin (200 pi x). Faux. y(5 10-3, x) =sin (-200 pi (5 10-3- x/5) = sin (pi-40 pi x) = sin (40 pi x).

retour -menu