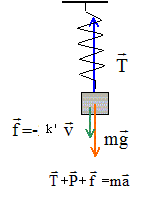|
Les oscillations mécaniques concours caplp interne 2009. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
La vérifications des performances mécaniques de la suspension d'une voiture dans le cadre du contrôle technique est obligatoire tous les deux ans. Un des éléments fondamentaux de cette suspension est constitué par le ressort. La constante de raideur du ressort ainsi que la période propre de l'oscillateur élastique représenté par le ressort, sont deux critères pris en compte lors de cette vérification.
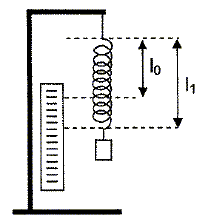
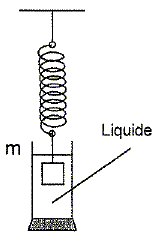
Un solide de masse m accroché à l'extrémité libre d'un ressort constitue un pendule élastique. On étudie l'quilibre de ce solide. Utiliser le dispositif ci-dessus, accrocher les différentes masses marquées à l'extrémité du ressort, noter les longueurs l1 prises par le ressort. Compléter le tableau ( g = 9,81 N/kg).
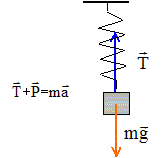
Déterminer la période propre de l'oscillateur ( masse + ressort). Proposer un protocol expérimental pour déterminer la période propre de l'oscillateur. Accrocher une masse m = 150 g ( par exemple) au ressort ; écarter la masse de sa position d'équilibre de quelques centimètres vers le bas, puis la lâcher. Mesurer la durée de 10 oscillations ( 10 périodes). Faire plusieurs mesures et calculer la moyenne. Etude de l'équilibre. Effectuer le bilan des forces qui s'exercent sur la masse marquée. Poids : verticale, vers le bas, valeur mg. Force de rappel exercée par le ressort, opposée au poids, valeur k(l1-l0) Le système étant à l'équilibre, énoncer le premier principe de Newton. Dans un référentiel galilen, un solide pseudo-isolé est : - soit au repos ( si la vitesse initiale est nulle) - soit son centre d'inertie est animé d'un mouvement rectiligne uniforme, et réciproquement. Ecrire la condition d'équilibre : mg = k(l1-l0) On écarte le solide de masse m d'une
distance xm au dessous de sa position
d'équilibre, puis on le laisse osciller
librement, après l'avoir lâché
sans vitesse initiale,à l'instant =0. Enoncer le second
principe de Newton. Dans un référentiel
galiléen, la somme vectorielle des forces
extérieures appliquées à un
solide est égale au produit de la masse M du
solide par l'accélération de son
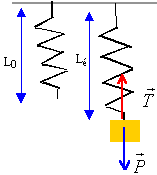
centre d'inertie. On note x(t) l'écart entre sa position à l'instant t et sa position d'équilibre.On prendra poids : vertical, vers le bas,
appliqué au centre d'inertie, valeur :
mg tension du ressort : verticale,
dirigée vers la position d'équilibre,
appliquée au point de fixation masse
ressort, valeur proportionnelle à la
déformation du ressort. à l'équilibre : mg =
k(Léq-L0) écarté de sa position
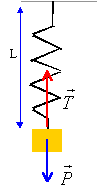
d'équilibre le ressort oscille : L=
Léq +x mg-k(L-l0)= m d²x/dt² mg-k( Léq +x-l0)= m
d²x/dt² mg-k( Léq -l0) - kx
=m d²x/dt² ; or mg =
k(Léq-L0) m
d²x/dt² + k x=0
(1) La solution de cette
équation peut se mettre sous la
forme x(t)=A cos(Bt) ou A
et B sont des constantes positives non nulles : Montrer que la période propre du pendule est : T0 = 2 p [m/k]½. w0 = [k/m]½ = 2 p /T0 ; d'où : T0 = 2 p [m/k]½ A.N : calculer le coefficient de raideur k, la période propre, la fréquence propre, la pulsation et écrire l'équation du mouvement. m =118 g ; l0 = 10 cm ; l1 = 12,7 cm ; xm = 1,8 cm ; g=9,81 N/kg. k = mg/(l1-l0) = 0,118*9,81 /(0,127-0,10) =42,87 ~42,9 N/m. T0 = 2 p [m/k]½= 6,28 [0,118/42,87]½=0,3296 ~0,33 s ; f0 = 1/T0 =1/0,3296=3,0 Hz ; w0 = [k/m]½ =[42,87/0,118]½ =19,0 rad/s. x(t) = 1,8 10-2 cos ( 19 t).
Ecrire l'expression de l'énergie mécanique du système masse ressort. On prend l'origine de l'énergie potentielle à la position d'équilibre x=0. EM = ½mv2 + ½kx2. Démontrer que l'énergie mcanique du système masse ressort est constante. Si x= xm, la vitesse est nulle, l'énergie mécanique est sous forme potentielle élastique EM = ½kxm2. En l'absence de frottement, l'énergie mécanique se conserve : EM = ½kxm2 =½mv2 + ½kx2 = constante. Calculer l'énergie mécanique du système. EM = ½kxm2 =0,5*42,87*0,0182 =6,9 10-3 J. Etude des oscillations amorties.
On note f = -a v la force de frottement fluide, où a est une constante et v le vecteur vitesse de la masse en translation verticale. Ecrire sans la résoudre l'équation différentielle qui traduit le second principe de Newton. L= Léq +x mg-k(L-l0)-av=
m d²x/dt² mg-k( Léq
+x-l0)-av=
m d²x/dt² mg-k( Léq -l0) - kx
-av =m d²x/dt²
; or mg =
k(Léq-L0) m d²x/dt²
+av
+ k x=0
avec v = dx/dt =
x' m
d²x/dt² +ax'
+ k x=0
(3)
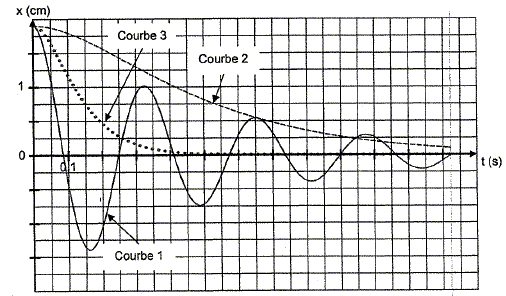
Pour les courbes 1 et 3 préciser la nature du mouvement observé ainsi que la grandeur que l'on peut déterminer sur la courbe 1 ; en déduire la valeur du coefficient a. (3) régime apériodique. (1) régime pseudo-périodique ; pseudo-période 2T = 0,65 s ; T = 0,325 s. d²x/dt² +2l x' + w20 x=0 ; équation caractéristique r2+2l r + w20 =0 ; discriminant D = 4l2-4w20. On pose w2 =w20 -l2; w =w0 [1-l2 /w20 ]½ ; T = T0[1-l2 /w20 ]-½ avec l= a /(2m) et T0 = 0,3226 s ( valeur issue du tableau suivant) (T0/T )2 =1-l2 /w20 ; l2 /w20 = 1-(T0/T )2 =1-(0,3226/0,325)2 =0,0147 ; l = 0,12 w0 =0,12*6,28/0,3226 =2,36 a = 2ml = 2*0,118*2,36 ~0,56. La courbe 2 correspond à un amortissement critique. Qu'est ce qu'un amortissement critique ? Quel est son intérêt ? Donner une application pratique. En mécanique ( véhicules) , le régime critique assure un meilleur confort aux passagers en évitant les oscillations ; le retour du système à l'équilibre est le plus rapide. Il en est de même en électricité, on évite des oscillations.
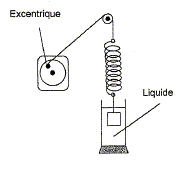
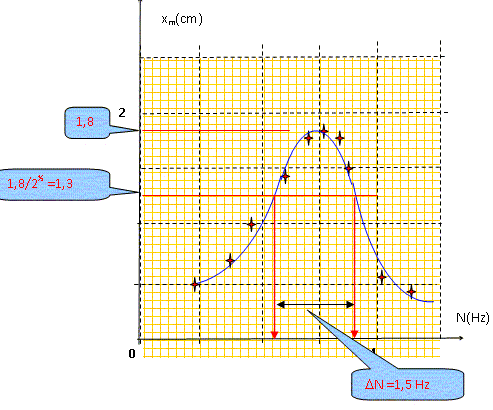
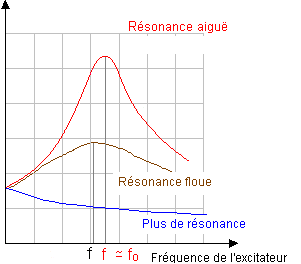
La courbe donnant les variations de l'amplitude des oscillations du résonateur en fonction de la fréquence qui lui est imposée par l'excitateur s'appelle courbe de résonance. Si l'amortissement augmente la fréquence de résonance diminue et la résonance devient plus floue. La résonance disparaît si l'amortissement devient très important.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|