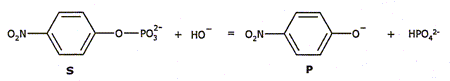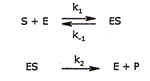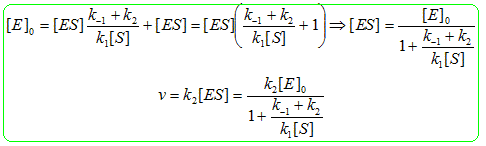Solution tampon, catalyse enzymatique concours Capes interne 2009

On se propose d'étudier la cinétique de la réaction totale d'hydrolyse du paranitrophénylphosphate ( noté S), composé incolore, en paranitrophénolate ( noté P), de couleur jaune en milieu basique. La réaction libère des ions hydrogénophosphate HPO42-. Le bilan de la réaction est le suivant : La réaction a lieu dans un milieu tamponné, à pH=9,8. Préparation de la solution tampon. Quelles sont les propriétés d'une solution tampon. Une solution tampon modère les variations de pH suite à l'ajout modéré d'un acide fort ou d'une base forte . Lors d'une dilution modérée, le pH d'une solution tampon ne varie pas. La solution tampon utilisée est un mélange d'un acide noté RNH3+ et de sa base conjuguée notée RNH2. Le pKa du couple est de 8,2 à 25°C. En notant c0 la concentration molaire totale du tampon, déterminer, en fonction de c0, les concentrations en RNH3+ et RNH2 notées respectivement ca et cb dans la solution tampon à pH=9,8. c0 = ca + cb et pH = pKa + log (cb /ca ) ; log (cb /ca )= pH-pKa =9,8-8,2 = 1,6 cb /ca = 101,6 =39,8 ; c0 = ca +39,8ca ; ca = 2,45 10-2 c0 ; cb=0,975 c0 ; Que peut-on penser des qualités d'une solution de pH=9,8 préparée à l'aide d'un couple acide /base de pKa = 8,2 ? Le pouvoir tampon est maximum lorsque pH = pKa. Ce nest pas le cas ici. La solution est préparée en introduisant une masse ma de l'acide, sous forme chlorure RNH3Cl et une masse mb de la base RNH2 dans une fiole jaugée de 1,00 L et en complétant avec de l'eau distillée. Calculer les masses ma et mb si c0 = 5,0 10-2 mol/L. M(RNH3Cl)=Ma =157,6 g/mol ; M(RNH2)=Mb =121,1 g/mol. ma = caMa =2,45 10-2* 5,0 10-2 *157,6 =0,193 g. mb = cbMb =0,975* 5,0 10-2 *121,1 =5,90 g. 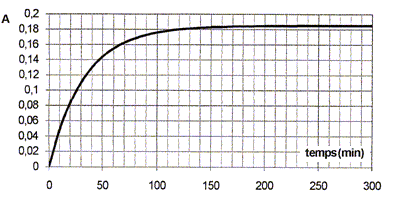Suivi cinétique de la réaction. La réaction S + HO- = P + HPO42- est suivie en mesurant l'absorbance du milieu réactionnel au cours du temps à la longueur d'onde l= 400 nm. A cette longueur d'onde seul P absorbe le rayonnement et l'absorbance suit la loi de Beer lambert. On réalise l'expérience avec une concentration initiale en substrat [S]0 = 10-5 mol/L. On enregistre l'évolution de l'absorbance au cours du temps. 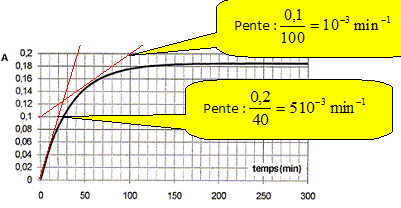La courbe obtenue est donnée ci-dessous :  On donne : coefficient d'absorption de P à 400 nm eP= 1,85 104 mol-1 L cm-1 ; longueur de la cuve : l=1,00 cm. Donner la définition de la vitesse volumique de la réaction. v = 1/V dx/dt= d[P]/dt avec V : volume (L) de la solution et x : avancement (mol) Exploiter la courbe pour en déduire la vitesse à t=0 et à t = 50 min. A = eP l [P] ; dA/dt = eP l d[P]/dt ; v = 1/(eP l)dA/dt v(t=0) = 1/(1,85 104)*5 10-3 =2,7 10-7 mol L-1 min-1 ; v(t=50) = 1/(1,85 104)* 10-3 =5,4 10-8 mol L-1 min-1. Comment la vitesse évolue t-elle au cours du temps ? Pour quelle raison ? La concentration des réactifs est un facteur cinétique : elle diminue au cours du temps ; la vitesse diminue donc au cours du temps. Définir le temps de demi-réaction et l'évaluer à partir de la courbe. 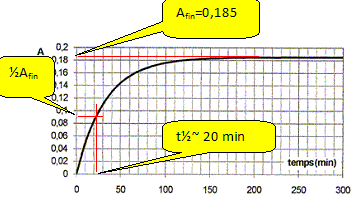Durée au bout de laquelle l'avancement est égal à la moitié de l'avancement final. Dans les conditions de l'expérience, la vitesse de la réaction suit la loi de vitesse : v = k[S]1. Quel est l'ordre de la réaction ? Quelle est la dimension de k ? La réaction est d'ordre 1 ; [k] =T-1. Montrer que [S(t)] est solution d'une équation différentielle du premier ordre. La résoudre pour exprimer [S] en fonction du temps, de [S]0 et de k. v = -d[S] /dt = k[S] ; d[S] /[S] = -kdt ; dln[S] = -kdt ln[S] -ln[S]0 = -kt ; [S] = [S]0 exp(-kt). En déduire l'expression du temps de demi-réaction en fonction de k. Evaluer k . ln(0,5[S]0 ) -ln[S]0 = -kt½ ; ln2 = kt½ ; t½ = ln2 / k ; k = ln2 / t½ =ln2 / 20 ; k ~ 3 10-2 min-1. Etude du modèle de Michaelis et Menten de la catalyse enzymatique. La réaction étudiée est catalysée par une enzyme, la phosphatase alcaline, que l'on notera E. Le mécanisme simplifié de la réaction catalysée est le suivant. Il est valable au début de la réaction. Chacune des étapes est élémentaire, les constantes k1, k-1 et k2 en sont les constantes de vitesse. Qu'est ce qu'un catalyseur ? Un catalyseur accélère une réaction thermodynamiquement possible ; il n'apparaît pas dans le bilan, étant régénéré en fin de réaction. On rappelle que la vitesse d'une étape élémentaire est une réaction avec un ordre dont les ordres partiels sont les nombres stoechiométriques. En déduire l'expression des vitesses v1, v-1 et v2 de chaque étape en fonction des constantes de vitesse et des concentrations en E, S et ES. v1 = k1 [S] [E] ; v-1 = k-1 [ES] ; v2 = k2 [ES]. Pourquoi peut-on dire que la vitesse de formation de P, et donc de la réaction s'écrit v = k2[ES]. L'étape 1 est un équilibre qui s'établit rapidement ; l'étape 2 est lente, c'est donc elle qui impose la vitesse. Le composé ES est un intermédiaire réactionnel, que l'on supposera suffisamment réactif pour pouvoir considérer que sa concentration reste constante au cours du temps. Dans ces conditions, on admet que :   Une concentration initiale d'enzyme [E]0 a été introduite au début de la réaction. A partir de la loi de conservation de la matière en enzyme et de la relation établie ci-dessus, exprimer la concentration [ES] en fonction de [E]0, [S] et des constantes de vitesse. Conservation de la matière de E : [E]0 = [E] +[ES] (1) d[ES]/dt = 0 = k1 [S] [E] -k-1 [ES] - k2 [ES]. [ES] = k1 [S] [E] / (k-1+ k2) [E] =[ES](k-1+ k2) / (k1 [S]), repport dans (1) : En déduire que la vitesse de réaction s'exprime sous la forme : v = vmax / (1+ KM/[S]) où vmax et KM sont des constantes de vitesse et de la concentration totale [E]0 en enzyme. vmax =k2[E]0 ; KM =(k-1+ k2) / k1. Dans quelle conditions retrouve t-on la loi de vitesse v = k[S]. Exprimer alors k en fonction de vmax et KM. Si KM/[S] est très supérieur à 1, v ~ vmax / KM [S] avec k = vmax / KM.

0,128

retour -menu