|
Etude d'une éolienne : la génératrice concours physique Capes 2009. |
|||||||
|
|||||||
|
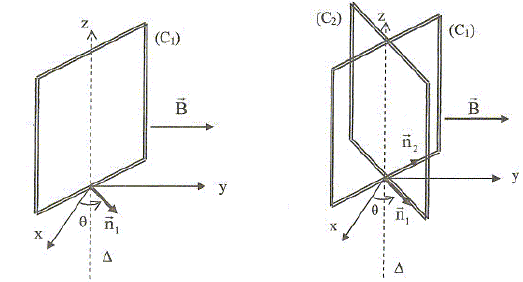
Les vecteurs sont écrits en gras et en bleu. l'axe de l'éolienne entraîne une génératrice qui fournit du courant électrique avec un rendement proche de l'unité. On schématise la génératrice par un cadre rectangulaire C1 sur lequel on a enroulé N spires. Ce cadre tourne dans un champ magnétique uniforme constant B = Bey autour d'un axe vertical que l'on trend comme axe Oz. On note n1 le vecteur normal, ce qui oriente le parcours du cadre. On note q l'angle orienté q =(ex,n1). Le cadre est entraîné par l'axe de l'éolienne et tourne à la vitesse angulaire W = q '.
j1
= B
.
Sc
n1
=Bey
.
Sc
n1 =
B Sc cos
(ey,n1)=
B Sc cos (p/2-q) j1
= B Sc sin
(q) Flux total à travers N spires : N j1 = N B Sc sin (q) e1 = -dj1 /dt = -N B Sccos (q) q '. L'enroulement de résistance et d'inductance propre négligeable, est connecté à une résistance R. Représenter le circuit électrique équivalent. Donner l'expression de i1, intensité du courant qui le parcourt.
Un second cadre identique C2, solidaire du premier et s'en déduisant par une rotation de 90°, complète le dispositif. On note n2 le vecteur normal à ce second cadre. Les deux cadres sont isolés électriquement l'un de l'autre. Exprimer la f.e.m e2 qui apparaît aux bornes de C2. Même calculs que ci-dessus en remplaçant q par ½p+q : e2 = -N B Sccos (½p+q) q ' =N B Scsin(q) q ' . Le cadre C2 est connecté à une résistance R de même valeur que celle connectée à C1. Etablir l'expression de l'intensité i2 circulant dans le cadre C2. i2 = e2/R =N B Scsin (q) q '/R.
On notera J le moment d'inertie par rapport à l'axe D de l'ensemble des deux cadres et de l'axe de l'hélice dont ils sont solidaires. On supposera que les liaisons avec l'axe sont parfaites. Calculer le moment G1 des forces de Laplace que subit le cadre C1. G1 =Ni1Scn1^ B = Ni1Sc B n1^ey = Ni1Sc B sin (p/2-q) ez = Ni1Sc B cos (q) ez. G1 = -N2 B2 S2ccos2 (q) q '/Rez. Calculer le moment G2 des forces de Laplace que subit le cadre C2. G2 =Ni2Scn2^ B = Ni2Sc B n2^ey = Ni2Sc B sin (-q) (ez) = -Ni2Sc B sin (q) (ez) . G2 = -N2 B2 S2csin2 (q) q '/Rez. Par application du théorème du moment cinétique par rapport à l'axe D, trouver une équation différentielle en q reliant les moments calculés ci-dessus et le moment Gm = Gm ez des actions exercées par l'hélice sur la partie tournante. Gm + G1 + G2 =ds0/dt ; projeter sur l'axe D : Gm + G1 + G2 = Jq".
Exprimer W en fonction de R, Gm, N, Sc et B. En déduire la puissance mécanique Pm fournie par l'hélice à la génératrice. W =q' ; en régime permanent W est constant, d'où dW/dt = 0 soit q'' = 0. par suite : Gm + G1 + G2 =0 ; Gm = - G1 - G2 =N2 B2 S2ccos2 (q) W /R + N2 B2 S2csin2 (q) W /R Gm =N2 B2 S2cW /R ; W =RGm /(N2 B2 S2c). Pm = Gm.W = GmW =RG2m /(N2 B2 S2c).
|
|||||||
|
|
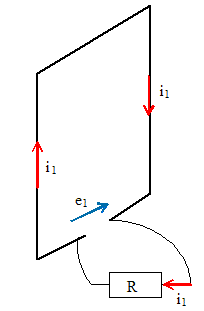 i1
= e1/R =-N B
Sccos (q)
q
'/R.
i1
= e1/R =-N B
Sccos (q)
q
'/R.