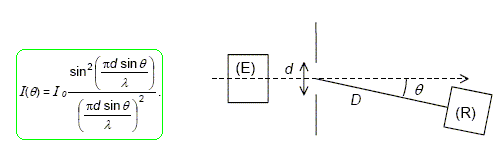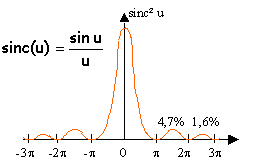Diffraction des ultrasons ; les ondes lumineuses ; concours physique capes 2004.

On envisage maintenant la propagation d'ultrasons de fréquence f = 40 kHz dans l'air à T = 293 K. L'onde, supposée plane, rencontre une ouverture ayant la forme d'une fente rectangulaire, de grande hauteur par rapport à la largeur, taillée dans une plaque métallique. La largeur de cette ouverture vaut d = 1 10-2 m On déplace un récepteur (R) sur un cercle de rayon D (distance entre l'ouverture et le récepteur) dans un plan contenant l'émetteur (E) et perpendiculaire au plan des plaques métalliques. On admet que l'intensité du son I(q) recueillie par le récepteur dans la direction q par rapport à l'axe médian "émetteur-fente" est de la forme : I0 étant l'intensité sur l'axe médian à la distance D de la fente (voir schéma). Tracer l'allure de la courbe représentant I(q) /I0 en fonction de sin q.   La fonction sinc² u s'atténue rapidement et s'annule tous les p. Pour q = 0, I(q) /I0 = 1 ; pour sin q = l / (2d), I(q) /I0 =0,41 ; pour sin q = l / d, I(q) /I0 =0. Calculer la valeur en degrés de l'angle q correspondant à I(q) /I0 =0,41, pour les ultrasons utilisés. sin q = l / (2d) avec l = c/f = 340/40000 =8,5 10-3 m ; sin q =8,5 10-3/0,02 =0,425 ; q =25°. Quelle devrait être la largeur " d' " de l'ouverture permettant d'obtenir le même rapport avec le même angle q pour des sons de fréquence 400 Hz. Commenter. l = c/f = 340/400 =0,85 m ; 2d = 0,85 / 0,425 = 2 , d = 1 m. Les sons audibles sont diffractés par des ouvertures de l'ordre du mètre ; les ultrasons sont diffractés par des ouvertures de l'ordre du centimètre. Les ondes lumineuses. Décrire une onde lumineuse dans le vide. C'est une onde électromagnétique dont la longueur d'onde sont comprises entre 400 nm et 800 nm. Propagation d'un champ magnétique et d'un champ électrique (l'un étant perpendiculaire à l'autre), dans un direction perpendiculaire au plan défini par les deux champs. Ce sont des ondes transversales dans le vide et dans les milieux homogènes. Qu’est ce qu’une lumière polarisée rectilignement ? Décrire sommairement une expérience de mise en évidence de cette polarisation rectiligne. Dans la lumière dite naturelle toutes les orientations du champ électrique, dans le plan perpendiculaire à la vitesse, sont équivalentes. Dans la lumière polarisée rectilignement, le vecteur représentatif du champ électrique reste parallèle à une direction fixe particulière. 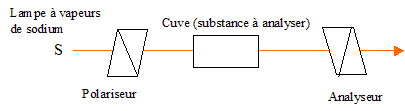L'axe de l'analyseur est perpendiculaire au polariseur. L'intensité de la lumière transmise par le dispositif est nulle. En remplissant la cuve d'eau, composé optiquement inactif, l'intensité de la lumière transmise est nulle. En remplissant la cuve d'une solution aqueuse de saccharose, composé optiquement actif, l'intensité de la lumière transmise n'est pas nulle : on retrouve une intensité nulle, en tournant l'analyseur d'un angle a.   Comparer qualitativement les ondes lumineuses et sonores. Ondes lumineuses : ondes électromagnétiques se propageant dans le vide à la célérité de 3 108 m/s. ondes sonores : onde mécanique progrssive ne se propageant pas dans le vide ; les célérités sont de l'ordre de 300 m/s à 5000 m/s. Donner la place des ondes lumineuses dans le spectre des ondes électromagnétiques. 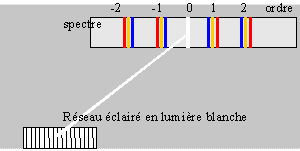Décrire ce que l’on observe lorsqu’un pinceau de lumière blanche traverse un réseau ; expliquer brièvement le phénomène. Définir l’indice d’un milieu transparent, homogène et isotrope. 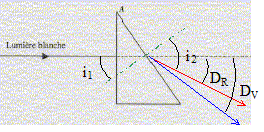indice n, nombre supérieur ou égal à 1, rapport de la vitesse de la lumière dans le vide à la vitesse de la lumière dans le milieu. De quelle manière celui du verre dépend-il de la longueur d’onde ? La formule de Cauchy donne l'évolution de l'indice d'un milieu en fonction de la longueur d'onde l de la radiation dans le vide. n= A+B/l² où A et B sont des constantes positives dépendant du milieu. L'indice du verre augmente lorsque la longueur d'onde diminue. Comment qualifie-t-on ce milieu ? milieu dispersif. Qu’en résulte-t-il pour un pinceau de lumière blanche qui traverse un prisme en verre ? Qu’observe-t-on ? Quelles sont les différences avec l’observation dans le cas du réseau ? 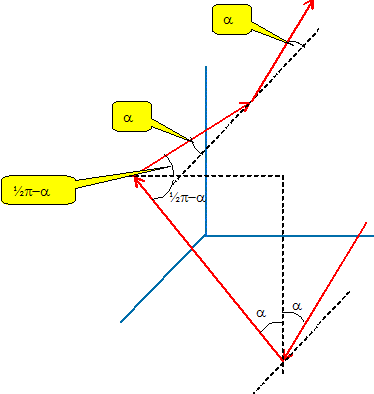l'angle d'incidence i1 vaut 30° ( des angles A et i1 à cotés perpendiculaires ont même mesure) seconde loi de Descartes pour la réfraction de la lumière rouge : nR sin i1 =nair sin i2. sin i2R = nR sin i1 =1,609 sin 30 = 0,804 ; i2R = 53,4° de même pour le violet : sin i2V = nV sin i1 =1,673 sin 30 = 0,836 ; i2V = 56,8° La déviation est la plus importante pour le violet ; on observe le contraire dans le cas d'un réseau. Énoncer les lois de Snell-Descartes. Rayons incident, réfléchi et réfracté sont dans le même plan. L'angle de réflexion est égal à l'angle d'incidence. Pour la réfraction : n1 sin i1 = n2 sin i2. Comment mesurer l’indice d’un solide ? d’un liquide ? On pourra décrire en quelques lignes une expérience réalisable par les élèves et/ou le principe d’un appareil de mesure. On envoie un faisceau de lumière monochromatique sur le bloc transparent : faire varier l'angle d'incidence i1 et noter les valeurs correspondantes de l'angle de réfraction i2. la pente du graphe sin i1 = f(sin i2) donne l'indice de réfraction du milieu . Télémétrie : mesure de la distance Terre-Lune. Pour réaliser cette mesure, on utilise un laser sur Terre qui émet des impulsions de durée t = 5.10-10 s vers un réflecteur posé sur la Lune constitué d’un nombre important de miroirs assemblés par 3 en occupant trois faces perpendiculaires entre elles d’un cube ( formant un trièdre trirectangle ). Pourquoi ne peut-on pas utiliser un simple miroir plan ? La lumière réfléchie ne sera pas dirigée vers l'émetteur terrestre. Montrer qu’un rayon lumineux arrivant sur un de ces miroirs est renvoyé vers la Terre après trois réflexions dans la même direction quelle que soit l’orientation du trièdre.   A partir de quelle taille typique peut-on négliger la diffraction par un obstacle ? sur ses bords ? Justifier votre réponse. Les dimensions de l'obstacle doivent être bien supérieure à la longueur d'onde de la lumière. Pour la tache centrale q = l/a ; q est proche de zéro si a < 100 l. En quoi les limites du modèle du rayon lumineux sont elles liées à la diffraction ? Un rayon lumineux est la représentation géométrique du trajet suivi par la lumière pour aller d’un point à l’autre. C’est une demi-droite, orientée dans le sens de propagation de la lumière, dont l’origine est un point source. Il est impossible, expérimentalement, d’isoler un rayon lumineux lumineux à cause du phénomène de diffraction. Le rayon lumineux est un modèle théorique limite : le faisceau laser réalise une bonne approximation d'un rayon lumineux tant que que celui-ci ne tombe pas sur des obstacles trop « petits » dont les dimensions sont de l'ordre de grandeur de la longueur d'onde du laser. Faire un schéma du dispositif permettant d’étudier la diffraction d’un faisceau laser par un cheveu. Sur ce schéma figureront toutes les notations utiles à cette étude. Donner l’allure de la figure de diffraction observée sur l’écran. Qu’y aurait-il de changé si le cheveu était remplacé par une fente de même dimension que le cheveu ? En vous tenant à vos notations, exprimer l’écart angulaire entre le milieu de la frange centrale et la première extinction du faisceau diffracté en fonction de l’épaisseur du cheveu et de la longueur d’onde du faisceau laser. Commenter cette relation. n place perpendiculairement au faisceau lumineux et à quelques centimètres du laser, une fente fine et horizontale de largeur a. Un écran situé à une distance D de la fente, montre des taches lumineuses réparties sur une ligne verticale. La tache centrale plus lumineuse que les autres, est la plus large. 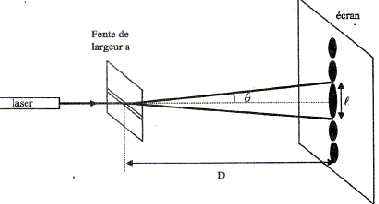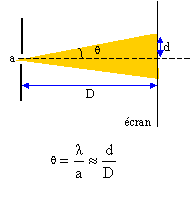La lumière émise par le laser est diffracté par le fente dont la largeur est du même ordre de grandeur que la longueur d'onde l. Par analogie avec les ondes mécaniques, cette expérience prouve le caractère ondulatoire de la lumière. Les observations sont identiques si le cheveu est par une fente de même dimemsion. L'angle q est donné par la relation : q =l/a ou demi écart angulaire correspondant à la tache centrale de diffraction. l et a s'expriment en mètre et q en radian. d'où d = lD/a ; en conséqence la largeur de la tache centrale " 2d= l " augmente lorsqu'on réduit la largeur "a" de la fente.

retour -menu