Le cyclotron Arronax d'après DTS IMRT 2009

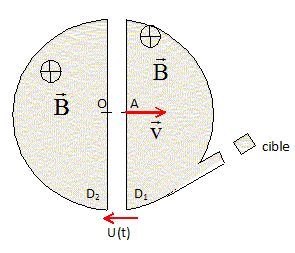
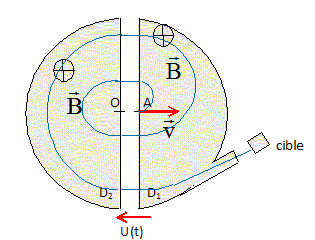
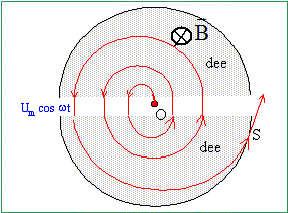
Un cyclotron est un instrument qui sert à accélérer des particules chargées, permettant ensuite de réaliser des expériences de physique nucléaire. Dans ce problème les particules chargées sont des protons. Le cyclotron est formé de deux deli-cylindre conducteurs creux appelés "dees" et sont déparés par un intervalle étroit. Un champ magnétique uniforme de valeur 1,5 T règne à l'intérieur de chaque "dees", sa direction est perpendiculaire au plan de la figure ci-dessous. Un champ électrique E variable dans le temps, peut être établi dans l'intervalle étroit qui sépare les "dees". Il permet d'augmenter la vitesse des protons chaque fois qu'ils pénètrent dans cet intervalle. Le champ électrique est nul à l'intérieur des "dees". On négligera la durée de transit entre les "dees". Le champ électrique variable est obtenu en appliquant une tension sinusoïdale entre les deux "dees", de valeur maximale UM=50 000 V de fréquence f. On injecte un proton au point O avec une vitesse négligeable. Il est alors accéléré par le champ électrique et pénètre dans le "dee" D1 au point A avec une vitesse v. ( On considère que le poids du proton est négligeable devant les autres forces en présence ). On démontre que le mouvement du proton est circulaire uniforme dans un "dee", de rayon R = mPv/(eB). 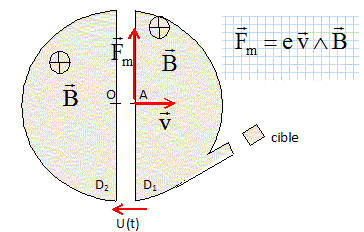Nommer la force à l'origine du mouvement circulaire uniforme à l'intérieur d'un des "dees" ? Donner son expression vectorielle puis la représenter en A ( sans soucis d'échelle). Force magnétique, force de Lorentz. Compléter la figure en représentant l'allure de la trajectoire d'un proton émis avec la vitesse v, jusqu'à la sortie du cyclotron après un nombre de tours arbitrairement choisis. ( aucun calcul n'est demandé)   ou encore :   Le rayon maximal de la trajectoire semi-circulaire dans le "dee" vaut Rm=0,67 m. Calculer alors la vitesse maximale vm puis l'énergie cinétique maximale E c max ( en J et en MeV) du proton à la sortie du cyclotron. ( o, considèrera le proton comme non relativiste ). 1 eV = 1,60 10-19 J ; masse du proton : mP= 1,67 10-27 kg. Rm = mPvm/(eB) donne : vm = Rm eB / mP. vm = 0,67*1,6 10-19*1,5 / 1,67 10-27 =9,629 107 ~ 9,6 107 m/s. Ec max = ½mPv2m = 0,5 * 1,67 10-27 *(9,629 107)2=7,74 10-12 ~ 7,7 10-12 J. 7,74 10-12 / 1,6 10-19 = 4,84 107 eV = 4,84 101 MeV~ 48 MeV. Etablir l'expression littérale de la durée d'un demi-tour dans un "dee". Calculer sa valeur. Les protons parcourent une demi circonférence de rayon r à la vitesse v de valeur constante : p r = v t½ avec r = mPv/(eB) soit r/v = mP/(eB) t½ = p r v = p mP eB t½ : valeur constante, indépendante de la vitesse. t½ = 3,14 * 1,67 10-27 / (1,60 10-19*1,5 ) = 2,186 10-8 ~2,2 10-8 s. Calculer, en justifiant, la fréquence f en MHz de la tension sinusoïdale. Pour une accélération maximale, à chaque demi tour, la tension alternative doit changer de signe et prendre sa valeur maximale. On négligera la durée de transit entre les "dees". La demi période de la tension alternative est égale à la durée d'un demi tour. T = 2t½ = 2p m / (eB) ; f = 1/(2t½) =1 / (2*2,186 10-8) =2,29 107 Hz f ~ 2,3 107 Hz ~23 MHz.

retour -menu