Corrosion du fer, machine frigorifique, capteur de température, Bts FEE 2009

Corrosion d'une cuve en acier (5 points) On recueille les eaux de ruissellement dans une cuve en acier (alliage de fer). Elle contient un volume d'eau : Veau = 10 m3. Donnée : constante d'autoprotolyse de l'eau : [H3O+][HO-]= 10-14 à 25°C.. L'eau de la cuve a un pH de 5,2. Calculer la concentration molaire en ions H3O+ et HO-. [H3O+] = 10-pH = 10-5,2 =6,3 10-6 mol/L. [HO-]= 10-14/[H3O+] =10-14/10-5,2 =10-8,8 =1,6 10-9 mol/L. Calculer la quantité de matière d'ions H3O+ présents dans l'eau. 10 m3 = 104 L ; n = Veau * [H3O+] =104 * 6,3 10-6 = 6,3 10-2 mol. On souhaite neutraliser l'eau de la cuve en ajoutant de la soude. Quelle est la valeur du pH de l'eau après neutralisation ? Dosage acide fort base forte : à l'équivalence le pH est égal à 7 à 25°C. Ecrire l'équation de la réaction de neutralisation entre les ions H3O+ et HO- . H3O+ aq+ HO- aq = 2 H2O (l). La cuve est à l'air libre et se corrode. Citer un agent responsable de la corrosion du fer. Le dioxygène de l'air. Ecrire la demi-équation électronique du couple Fe2+/ Fe. Fe2+aq+ 2e- = Fe(s) L'eau de la cuve contient du dioxygène dissous. La demi-équation électronique du couple O2 aq / H2O(l) s'écrit : O2 aq + 4H+aq + 4e- =2 H2O(l) Donner l'équation chimique de la réaction entre le dioxygène dissous dans l'eau et le fer. O2 aq + 4H+aq + 4e- =2 H2O(l) 2 Fe(s) = 2Fe2+aq+ 4e- Citer une méthode de protection de la cuve contre la corrosion. Recouvrir le fer d'une epinture antirouille ; relié le fer à une anode sacrificielle en magnésium. Principe d'une machine frigorifique. (8 points) Le fluide frigorigène subit les transformations réversibles suivantes : - en A, (entrée du compresseur ) la vapeur saturée, est à la température T1 = 243 K et à la pression p1 =1,51 bar. Elle est comprimée adiabatiquement jusqu'à la pression p2 =5,67 bar (trajet A-B : compresseur). On note T2 la température du fluide en B. - La vapeur sèche subit une transformation isobare dans le condenseur jusqu'à liquéfaction totale (trajet B-C). - En C, le fluide est à l'état de liquide saturé à la température T3 = 293 K . Il est détendu de manière isenthalpique jusqu'à la pression p1. (trajet C-D). - Enfin, le fluide entre dans l'évaporateur où le liquide restant se transforme en vapeur saturée à la température T1 = 243 K (trajet D-A). Données : le fluide dans son état gazeux se comporte comme un gaz parfait. 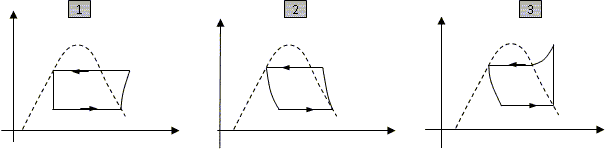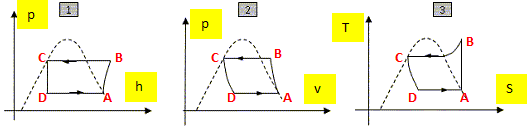Rapport des chaleurs massiques : g= cP/cV =1,2 ; cP = 480 J kg-1 K-1. A B C D T(K) T1 = 243 T2 T3 = 293 T1 = 243 p(bar) p1 =1,51 p2 =5,67 p2 =5,67 p1 =1,51 h(kJ kg-1) 338 hB 219 hD Sur la figure du document annexe (à rendre avec la copie), choisir les couples de grandeurs (p, v) ; (p, h) et (T, s) adaptés à chaque graphe et placer les grandeurs sur les axes correspondants. Placer les points A, B, C et D sur chacun des trois graphes. Dans une machine frigorifique, le cycle est décrit dans le sens anti-horaire. Dans le diagramme (T s ) la compression adiabatique A --> B, correspond à un segment vertical. La température augmente de T1 à T2. Dans le diagramme (p h ) la détente isenthalpe C --> D, correspond à un segment vertical. Dans le diagramme (p v ) la transformation isobare B --> C, correspond à un segment horizontal. La pression de la vapeur sèche à la sortie du compresseur est p2 = 5,67 bar . Montrer que la température T2 du fluide en fin de compression est égale à 303 K. Transformation adiabatique réversible A--> B : PVg = cste. Loi des gaz parfaits PV = nRT ; V = nRT/P d'où : P1-g Tg = cste ; P(1-g) / g T = cste. P1(1-g) / g T1 =P2(1-g) / g T2 ; T2 =T1 [P1 / P2](1-g) / g T2 =243 [1,51/5,67]-0,2/ 1,2 =243*1,246 =303 K. En utilisant le premier principe de la thermodynamique, établir l'expression du travail massique fourni par le compresseur au fluide (travail de transvasement) en fonction de cP , des températures T1 et T2 puis faire l'application numérique. DhAB = WAB + QAB avec QAB = 0 ( adiabatique) et DhAB =cp ( T2-T1) WAB =cp ( T2-T1) = 480 (303-243) =28,8 103 ~ 29 kJ kg-1. En déduire la valeur de l'enthalpie massique du fluide au point B. DhAB =hB-hA ; hB = hA + DhAB =338 + 28,8 = 366,8 ~ 3,7 102 kJ kg-1. Exprimer littéralement la quantité de chaleur massique cédée par le fluide, entre les points B et C, en fonction de cP , T2,T3 et L (chaleur latente de liquéfaction à la température T3 ). Faire l'application numérique en prenant L = -143 kJ kg-1. Transformation isobare dans le condenseur : QBC = DhBC + L = cp(T3-T2) + L. QBC = 480 (293-303) -143 103 = (-4,8 -143)103 = -147,8 kJ kg-1 ~ 1,48 102 kJ kg-1. On donne l'enthalpie massique du liquide saturé à la pression p1=1,51 bar et à la température T1 =243 K ; hliq =173 kJ kg-1. Déterminer l'enthalpie massique du fluide au point D.  "isenthalpique jusqu'à la pression p1. (trajet C-D)" DhCD =0 ; hD-hC = 0 ; hD=hC =219 kJ kg-1. Déterminer le titre vapeur xv en ce point. xV = (hD-hliq) / (hA-hliq) =(219-173) / (338-173) = 0,279 ( 28 %). Exprimer l'efficacité de ce système réfrigérant en fonction des enthalpies massiques hA, hB et hD. Faire l'application numérique. Chaleur retitée à la source chaude / travail investi = QDA / WAB = (hA-hD) / WAB. efficacité = (338-219) / 28,8 = 4,1. Un capteur de température. 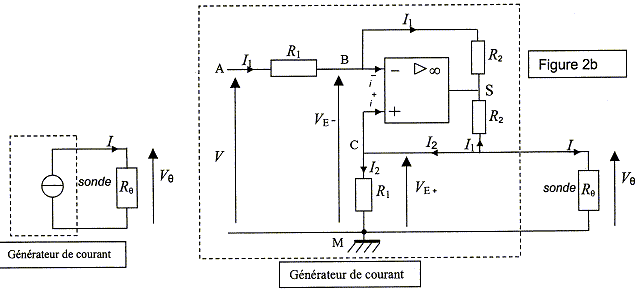Le capteur de température est constitué par une résistance Rq alimentée par un générateur de courant. 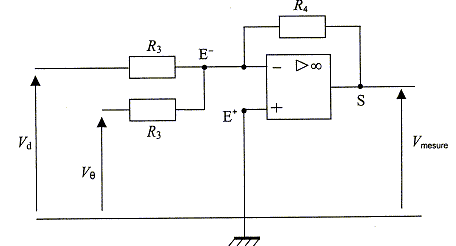Pour des températures q comprises entre -50°C et +100°C , la résistance du capteur est donnée par la relation Rq =R0(1+a q ) avec R0=100 ohms et a=4,0 10-3°C-1. Dans tout le problème, les amplificateurs opérationnels sont parfaits, ils fonctionnent en régime linéaire ; ainsi : VE+=VE-=Vq ; i+ = i- =0 ; Vsat+ = + 15 V ; Vsat- = -15 V. Etude du générateur de courant. Le capteur est traversé par un courant d'intensité I constante, produit par un générateur de courant. On donne R1 =1,0 kW, R2 =10,0 kW et V = 1,0 V. Les deux résistances R2 sont traversées par des courants ayant la même intensité (représentée par I1 sur le schéma). Exprimer I1 en fonction de V, VE+ et R1. V = R1 I1 + VE+ ; I1 = (V-VE+ ) / R1. Exprimer I2 en fonction de VE+ et R1. VE+ = R1I2 ; I2 = VE+ / R1. En déduire que l'intensité I du courant dans la sonde a pour expression : I = -V/R1. Calculer sa valeur numérique. Loi des noeuds : I1 + I2 +I = 0 ; I = -I1 - I2 =[- (V-VE+) -VE+ ] / R1 = -V/R1 = - 1,0 / 1,0 103 = -1,0 10-3 A. Quel est l'intérêt de maintenir l'intensité I constante dans la résistance ? Vq = RqI ; si I est constante, la tension aux bornes du capteur est proportionnelle à Rq ; Rq - R0 est de plus proportionnelle à la température. Montrer que la tension Vq aux bornes du capteur peut s'écrire : Vq =-0,10 -4,0 10-4 q. En déduire les valeurs de Vq pour q= 0°C et pour q= 100°C. Vq = RqI = -RqV / R1 =-R0(1+a q )V / R1 = -100(1+4,0 10-3q )*1,0 / 1,0 103 = -0,10 - 4,0 10-4q. V0 = -0,10 V ; V100 = -0,14 V.   Obtention d'une tension proportionnelle à la température. On veut obtenir une tension Vmesure proportionnelle à la température q ; soit Vmesure = K q. On donne : R3 = 1,0 kW et Vd est une tension continue ajustable. La tension de sortie du montage représenté sur la figure pour expression : Vmesure =-R4/R3 (Vd+Vq) On fixe Vd= 0,10 V . Montrer que Vmesure = K q et donner l'expression de K en fonction de la résistance R4. Vmesure =-R4/R3 (Vd+Vq) et Vq=-0,10 - 4,0 10-4q ; avec R4 exprimée en kW. Vmesure = -R4 (0,10 -0,10 - 4,0 10-4q) = 4,0 10-4 R4 q ; K = 4,0 10-4 R4. Quelle valeur doit avoir R4 pour obtenir une tension de sortie Vmesure =10 V à la température q = 100°C ? R4 = Vmesure / (4,0 10-4q) = 10 / 0,04 =250 kW.

retour -menu