Les murs capteur et Trombe, hydraulique ( Bernoulli), matière plastique : Bts bâtiment 2009.

. Ce sujet qui comporte 3 parties indépendantes porte sur le principe d'un dispositif appelé "mur capteur " qui utilise l'énergie solaire pour chauffer une pièce. Ce dispositif est constitué d'une baie vitrée située à quelques centimètres à l'extérieur d''un mur en béton exposé au sud. La face extérieure du mur en béton est peinte en noir. Le mur Trombe est un mur capteur qui possède en plus des  ouvertures horizontales hautes et basses qui perrnettent à l'air de la pièce  de se réchauffer en circulant dans la zone " chaude "située entre le mur en béton et le vitrage. La coupe latérale d 'un mur capteur à l'allure suivante ( sans souci d'échelle ) : 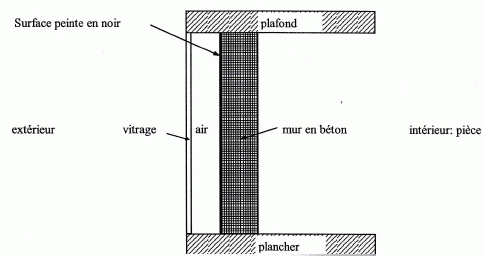Par construction, le simple vitrage, la lame d 'air emprisonné entre le vitrage et le mur en béton ainsi que le mur en béton ont des dimensions communes : longueur L : 3,00 m et de hauteur  h : 2,50 m. Seule l'épaisseur des diverses couches varie. Le simple vitrage a pour épaisseur : everre = 4,00 mm Le mur en béton a pour épaisseur : ebéton = 30,0 cm La lame d 'air emprisonné a pour épaisseur : eair =10,0 cm. Thermique (8 points)   Pour comprendre l'intérêt de la couche d 'air, on suppose, pour le début de la prernière question, qu'elle n'existe pas. Exprimer littéralement la résistance thermique surfacique notée Rr de I'ensemble {mur +vitrage) (on suppose ici que l'épaisseur de la lame d 'air emprisonné  est nulle). On notera les conductivités thermiques et les résistances thermiques surfaciques superficielles avec les notations introduites ci-dessous : lverre = 1,15 W m-1 K-1 ; lbéton = 1,75 W m-1 K-1 ; Les valeurs des résistances thermiques surfaciques superficielles sont : rse= 0,0600 m2 K W-1 entre l'air extérieur et la vitre   rsi1= 0,110 m2 K W-1  entre le mur en béton et  l'air intérieur de la pièce. Rr =  rse  + everre / lverre + ebéton  / lbéton +rsi1. Calculer la valeur de la résistance thermique surfacique R1. R1 =0,0600 + 4,00 10-3 / 1,15 +0,300 / 1,75 +0,110 = 0,0600+ 3,478 10-3 +0,1714 +0,110 =0,345  m2 K W-1. Calculer la résistance thermique surfacique notée R2 de l'ensemble {mur+ air emprisonné + verre}. lair =0,026W m-1 K-1 ; rsi2= 0,0500 m2 K W-1 entre la vitre et l'air emprisonné   rsi3= 0,100 m2 K W-1  entre le mur en béton et  l'air emprisonné. R2 =  rse  + everre / lverre + rsi2 + eair / lair + rsi3+  ebéton  / lbéton +rsi1. R2 = R1 + rsi2 + eair / lair + rsi3 =0,345 +0,05 +0,100 /0,026 + 0,100 R2 =4,34  m2 K W-1. En comparant les valeurs de R1 et R2 conclure quant  à l'intérêt de la couche d'air. En présence de la couche d'air la résistance thermique surfacique  est 12,5 fois plus grande. Le flux thermique des pertes sera donc 12,5 fois plus faible. On suppose, qu'un jour dhiver, la température extérieure est de 5,00 °C et que la ternpérature intérieure est de 19,0° C. Calculer la valeur de l'aire S de la surface du vitrage (qui est aussi celle du mur en béton et de la couche d'air emprisonné). S = L h = 3,00 * 2,50 =7,50 m2. Dormer la formule littérale qui permet de calculer le flux J des pertes de puissance occasiormée par ce dispositif capteur. J =K S Dq avec K = 1/R2 et Dq = 19-5 = 14,0 °C.  Calculer la valeur de ce flux. J =1/4,34 *7,50 *14,0 =24,2 W. Ce dispositif n'empêche donc pas les pertes mais il les réduit. D'autre part, il permet de capter une partie de l'énergie solaire qui aurait été renvoyée vers I'extérieur par un mur classique: c'est l'origine de son nom "mur capteur". Rappeler les valeurs extrêmes de longueur d'onde ou de fréquence des radiations dites " visibles". 400 nm  ( limite avec l' UV) et 800 nm ( limite avec l'IR). Placer sur un axe orienté, en longueur d 'onde ou en fréquence le domaine du " visible" et celui des " infra rouges" (noté IR) Donner le nom de l'effet qui prend place entre le vitrage et la face du mur peint en noir ? Le béton, à forte inertie thermique, accumule le rayonnement solaire le jour et le restitue pendant la nuit. Devant le béton, on place une vitre afin de créer un effet de serre qui chauffe l'air emprisonné. Mécanique des fluides (6 points) Sur certains types de murs capteurs, on pratique des ouvertures horizontales (aussi appelés évents) dans  les parties basses et hautes du mur en béton, le dispositif s'appelle alors "mur Trombe" (du nom de son inventeur). On suppose que les ouvertures, situées dans la partie haute du mur, ont le profil suivant ( en vue transversale, sans souci d 'échelle ). 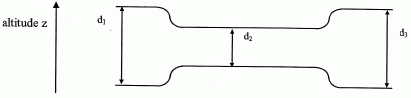On suppose que I'air ascendant situé entre la vitre et le mur arrive à l'entrée, de diamètre d1= l0 cm, d'un évent supérieur avec une vitesse v1=20 cm.s-1. Le diamètre intérieur de 1'évent d2 vaut la moitié de d1 . Le diamètre de sortie de l'évent (côté intérieur) a la même valeur que celui de I'entrée d3 = d1. Rappeler l'expression de l'équation, dite de continuité, qui traduit la conservation du débit volumique, noté Qv en fonction de S (surface) et v (vitesse). Qv = S v = constante. Qv = 0,25  pi d12 v1 =0,25  pi d22 v2 . Grâce à cette relation et à l'énoncé, montrer que la vitesse à I'intérieur de l'évent, notée v2, vaut 80 cm.s-1. d12 v1 =d22 v2 ; v2 =  v1 [d1/d2 ]2 d1 = 2 d2 ; v2 =  v1 [2 ]2 = 4 v1  = 80 cm.s-1. Grâce à la géométrie de la conduite, donner la valeur de la vitesse de I'air v3, à la sortie de l'évent. Le diamètre de sortie de l'évent (côté intérieur) a la même valeur que celui de I'entrée d3 = d1. d12 v1 =d32 v3 ; v3 =  v1 = 20 cm.s-1.   Web www.chimix.com Afin de commander simplement l'ouverture et la fermeture de l'évent supérieur, on cherche  à déterminer l'écart de pression entre  l'intérieur de l'évent supérieur et  la pièce ( sortie de l'évent supérieur ). Donner l'équation de Bernoulli en absence de machine hydraulique. p/r + gz + ½v² = constante ; g représente la valeur du champ de pesanteur terrestre. En déduire que l'expression de la dépression entre la pression P2 (à 1'intérieur de l'évent) et P3 (pression à la sortie de l'évent) en fonction de v1 peut s'écrire : P2 -P3 =-7,5 r v12. Les deux évents sont  à la même altitude : les termes gz  vont donc s'annuler. P2 / r + ½v22 = P3 / r + ½v32 avec  v3 = v1 et  v2 = 4v1. P2 / r + 8v12 = P3 / r + ½v12 ; P2 -P3 = -7,5 r v12 . Calculer cette dépression. On donne la valeur de la masse volamique r de l'air 1,2 kg.m-3. P2 -P3 =-7,5 r v12 = -7,5 *1,2 * 0,202 = -0,36 Pa. La partie interne de l'évent à une surface d'aire A = 750 cm2. Calculer la force due à la dépression sur cette surface. F = A | P2 -P3| avec A = 0,075 m2. F = 0,075*0,36 =0,027 N. Sans justification, choisir le matériau utilisé pour fabriquer un panneau, d'aire A, (positionné à la frontière entre 1a partie interne de l'évent et sa sortie) qui s'ouwirait sous I'effet d'une dépression de l'ordre de 0,35 Pa : - bois (épaisseur 4 cm ), soie( épaisseur 0,8 mm), caoutchouc( épaisseur 5 cm). Pour réaliser la baie vitrée, le propriétaire décide d'utiliser une vitre en plastique incassable composée entre autre d'un polymère  de formule : --( CH2--CF2 )n-- ( n est un entier naturel). Donner la définition d'un polymère. Macromolécule  obtenue   à partir d'un grand nombre de petites molécules ( monomère) , associées par liaisons de covalence. Ce polymère est obtenu à partir du monomère dont la formule développée est la suivante : Donner l 'équation de réaction traduisant le passage du monomère au polymère. n H2C=CF2  ---> --( CH2--CF2 )n-- Quel nom donne-t-on à  n ? L'indice moyen de polymérisation.  Déterminer sa valeur. On donne : La masse molaire du polymère est de 96 kg.mol-1 et les masses molaires atomiques suivantes : H : 1,0 ; C : 12 ; F  : 19 g/mol. Masse molaire du monomère : M = 2*12+2+2*19 = 64 g/mol n = 96 000 / 64 =1500 = 1,5 103. On dispose d 'une rnasse m1 =500 kg de monomère. Combien peut-on obtenir, de masse m2 de polymère, sachant que le rendement de la réaction est de 90 %. Si le rendement était de 100 %, 500 kg de monomère donnerait 500 kg de polymère. Pour un rendement de 90 % : m2 = m1*0,9 = 500*0,9 = 450 kg = 4,5 102 kg.

retour -menu