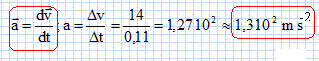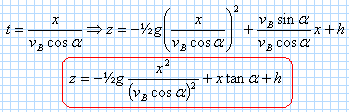|
Le hockey sur gazon ( bac S Amérique du Nord 2009) voir le site du lycée Rochambeau |
|||||||
|
|||||||
|
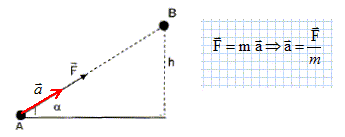
On étudie le mouvement de la balle de centre d'inertie G et de masse m, dans le référentiel terrestre supposé galiléen. Cette étude est décomposée en deux phases. Phase 1. Dans cette phase on néglige toutes les actions liées à l'air ainsi que le poids de la balle. Au point A la balle est immobile. Entre les points A et B elle reste en contact avec la crosse. La force F exercée sur la balle par la crosse est supposée constante. Le segment AB représentant la trajectoire de la balle est incliné d'un angle a = 30° avec l'horizontale. On donne : m = 160 g ; g = 9,8 m s-2. Enoncer la seconde loi de Newton et l'appliquer à la balle lors de son trajet entre A et B. Dans un référentiel galiléen, la somme vectorielle des forces extérieures appliquées à un solide est égale au produit de la masse M du solide par l'accélération de son centre d'inertie. "Dans cette phase on néglige toutes les actions liées à l'air ainsi que le poids de la balle" Que peut-on dire du
mouvement de la balle entre A et B. La force et la masse sont constantes : le
vecteur accélération est donc
constant. Entre A et B, le mouvement de la balle est
uniformément
accéléré.
Donner l'expression du vecteur accélération en fonction du vecteur vitesse. Calculer la valeur de l'accélération.
Calculer l'intensité de la force exercée sur la balle par la crosse. L'hypothèse concernant le poids de la balle est-elle justifiée ? F = m a avec m = 0,160 kg et a = 1,27 102 m s-2. F = 0,160 * 127 = 20,3 ~ 20 N. Poids P = mg = 0,160*9,8 = 1,6 N, environ 13 fois plus faible que la valeur de la force F. L'hypothèse concernant le poids est justifiée.
On écrit les vecteurs en gras et en bleu. Au point B, la balle quitte la crosse à la date t=0 avec le vecteur vitesse vB contenu dans le plan (xOz) : c'est la seconde phase du mouvement dans laquelle on néglige toutes les actions liées à l'air. On étudie le mouvement du centre d'inertie de la balle dans le champ de pesanteur supposé uniforme. L'axe Ox est horizontal dirigé vers la droite. L'axe Oz est vertical dirigé vers le haut. L'origine des axes est à la verticale du point B telle que OB= h = 0,40 m.
Donner l'expression des coordonnées vBx et vBz du vecteur vitesse de la balle à la date t=0. vBx= vB cos a et vBz = vB sin a. Donner l'expression des coordonnées xB et zB du vecteur OB de la balle au point B. xB= 0 et zB = h. En appliquant la seconde loi de Newton on obtient les équations horaires suivantes : a ( ax=0 ; az = -g) ; v ( vx=vB cos a ; vz = -gt +vB sin a) ; Montrer que la valeur vS de la vitesse de la balle au sommet S de la trajectoire est vS= 12 m/s. Au sommet de la trajectoire le vecteur vitesse est horizontal : sa composante verticale est donc nulle. vS = vx=vB cos a = 14 cos 30 = 12,12 ~ 12 m/s. Montrer que les coordonnées du vecteur position OG du centre d'inertie de la balle sont : x = vB cos a t ; z = -½gt2 + vB sin a t + h. Le vecteur position est une primitive du vecteur vitesse : x = vB cos a t + constante ; or à t=0 x(t=0) est nul : la constante d'intégration est donc nulle. z = -½gt2 + vB sin a t +constante ; or à t=0, z(t=0) = h : la constante d'intégration est égale à h. En déduire l'équation de la trajectoire de la balle.
Quelles conditions doivent satisafaire x et z pour que le but soit marqué ? Vérifier que ces contitions sont bien réalisées. Lorsque x supérieur ou égal à 15 m, la valeur de z doit être inférieure à 2,14 m. z( 15) = -½*9,8 *152 / ( 12,122) + 15 tan 30 + 0,40 =-7,505 + 8,66 +0,40 = 1,56 ~1,6 m.
|
|||||||
|
|