Bobine d'un woofer : méthode d'Euler bac S Amérique du sud 2008.

Frédéric, un élève bricoleur, démonte le caisson de grave de sa chaîne Hi-fi. Cette enceinte acoustique comporte un woofer : c'est un haut parleur de grand diamètre qui a pour fonction de reproduire les sons graves. Frédéric découvre à l'intérieur du woofer une bobine formée d'un enroulement de fil de cuivre isolé sur le cylindre en carton. Il montre cette bobine à son professeur de sciences physiques et lui demande comment trouver les valeurs de l'inductance L et de la résistance interne r de cette bobine. Le professeur lui propose de trouver expérimentalement les caractéristiques de la bobine du woofer lors d'une séance de travaux pratiques. 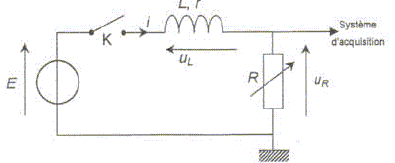Frédéric dispose du matériel suivant : Un générateur de tension continue de f.e.m. E = 6,0 V ; un conducteur ohmique de résistance R réglable ; la bobine du woofer ; un interrupteur ; des fils de connexion et un système d'acquisition informatisé. Frédéric réalise le montage représenté ci-dessous. Il règle la résistance à la valeur R = 10 ohms. A l'instant de date t = 0 s, il ferme l'interrupteur et enregistre la courbe d'évolution de la tension uR aux bornes du conducteur ohmique en fonction du temps. 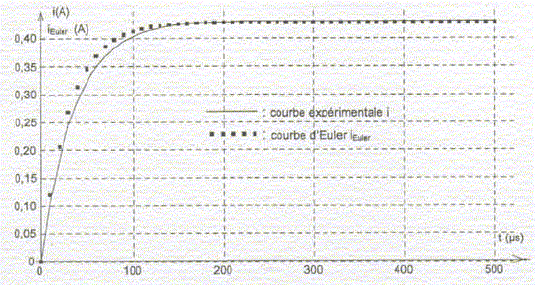Partie A : Le professeur : " À partir de la courbe que vous venez d'enregistrer, vous pouvez utiliser les fonctions du logiciel pour faire apparaître la courbe d'évolution de l'intensité du courant en fonction du temps. " Frédéric obtient la courbe suivante. Frédéric : " Cette nouvelle courbe a la même allure que celle obtenue lors de mon acquisition : elle comporte deux parties correspondant au régime transitoire et au régime permanent. En utilisant le régime permanent, je devrais pouvoir trouver la valeur de la résistance interne r de la bobine ". Après quelques calculs, Frédéric trouve r = 4,0 ohms. Le professeur : " Il existe un appareil permettant de vérifier si votre résultat est juste. Réfléchissez ". À partir de la courbe qu'il a enregistrée, expliquer comment Frédéric a pu obtenir la courbe donnant l'évolution de l'intensité du courant en fonction du temps. L'intensité qui traverse un conducteur ohmique et la tension aux bornes de ce conducteur sont proportionnelles. En divisant UR par la valeur de R = 10 ohms, on obtient l'intensité i. Quelle est la valeur de l'intensité I du courant traversant le circuit lorsque le régime permanent est atteint ? Equation de l'asymptote horizontale ( correspondant au régime permanent) I = 0,43 A. Montrer que l'expression de l'intensité I du courant en régime permanent est : I = E / (R+r) . Vérifier la valeur de la résistance interne r de la bobine du woofer. Tension aux bornes du conducteur ohmique UR = R I, en régime permanent. Tension aux bornes de la bobine UL = Ldi/dt + ri. En régime permanent l'intensité étant constante, sa dérivée par rapport au temps est nulle d'où UL = rI. Additivité des tensions : E = uR + uL = RI + rI. I= E R+r d'où r = E I -R = 6,0 0,43 -10 = 4,0 ohms. Quel appareil Frédéric peut-il utiliser pour vérifier que la résistance interne de la bobine du woofer est r = 4,0 ohms ? Multimètre utilisé en ohmmètre. Partie B : Le professeur : " Maintenant, comment pouvez vous trouver l'inductance L de la bobine en utilisant encore une fois la courbe ci-dessus ? " Frédéric : " Et si je déterminais graphiquement la constante de temps du circuit ? " Le professeur : " C'est une bonne idée ! Ne soyez pas étonné, ce genre de bobine a une valeur d'inductance assez faible de l'ordre du millihenry ". A partir de la courbe et en détaillant votre méthode, déterminer la constante de temps t du circuit. Donner l'expression de la constante de temps t en fonction des grandeurs caractéristiques du circuit. En déduire la valeur de l'inductance L de la bobine du woofer. t = L R+r d'où L = (R+r) t = 14*35 10-6 ~ 4,9 10-4 ~0,49 mH. Partie C : Le professeur : " Il nous reste encore un peu de temps avant la sonnerie : je vous propose d'étudier de manière théorique l'établissement du courant dans le circuit représenté sur la figure ". Frédéric : " J'applique la loi d'additivité des tensions et j'obtiens une équation de la forme : di dt =A-B i(t) (équation 1) " Le professeur : " Vous allez résoudre numériquement l'équation 1 par la méthode d'Euler. Je vais vous donner les valeurs de A et de B. Je vous prépare un tableau pour que vous fassiez les premiers calculs à la main ". Frédéric : " Monsieur, c'est long ! " Le professeur : " Continuez vos calculs à l'aide du tableur de l'ordinateur ". Établir l'équation 1 et vérifier que les expressions littérales de A et B sont : A= E L et B= R+r L Tension aux bornes du conducteur ohmique UR = Ri, Tension aux bornes de la bobine UL = Ldi/dt + ri. Additivité des tensions : E = uR + uL =( R + r)i + Ldi/dt. di dt = E L - (R+r) i L Établir, à l'aide d'une analyse dimensionnelle, l'unité de B dans le système international. (R+r) : énergie divisée par une intensité au carrée et par un temps. L : inductance = énergie divisée par une intensité au carré. R+r L = énergie I2 t * I2 énergie = 1 temps B s'exprime en s-1. On donne A = 1,2 104 A.s-1 et B = 2,8 104 SI La méthode d'Euler permet de calculer successivement les valeurs de i(t) et de di/dt à des instants de date t séparés par des intervalles de temps réguliers Dt. D t est le pas de résolution du calcul, ici D t = 1,0 10 -5 s. 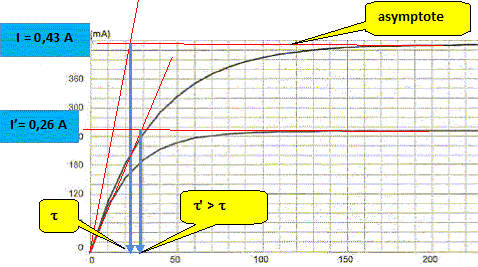Compléter le tableau suivant : t(s) i(A) di/dt ( A s-1) 0 0 1,2 104 1,0 10-5 0,12 8,6 103 2,0 10-5 0,21 6,1 103 A la date t=0, l'intensité est nulle d'où : di dt = 1,2 104- 2,8 104 *0 = 1,2 104 A la date t=1,0 10-5 : di dt = 1,2 104- 2,8 104 *0,12 =8,6 103 A la date t=2,0 10-5 : 6,1 103 = 1,2 104- 2,8 104 i(t) i(t) = (1,2 104-6,1 103 )/ 2,8 104 = 0,21 A A l'aide d'un tableur, Frédéric continue les calculs jusqu'à l'instant de date t = 500 µs. Il place les valeurs expérimentales i(t) et les valeurs calculées iEuler(t) par la méthode d'Euler sur le graphe ci-dessus. Partie D : Frédéric : " Monsieur, que s'est-il passé ? J'ai une courbe supplémentaire sur mon écran ! " Le professeur : " Pendant que vous faisiez vos calculs à la main, j'ai effectué une nouvelle acquisition. J'ai gardé dans le circuit la bobine de votre woofer et je n'ai modifié qu'une seule grandeur caractéristique du circuit ". Frédéric : " Vous avez changé soit la valeur de la f.e.m. E du générateur, soit la valeur de la résistance réglable R ". Le professeur : " Et oui ! Comparez les constantes de temps des deux courbes et vous trouverez ce que j'ai modifié dans votre montage ". La courbe obtenue par le professeur est représentée ci-dessous : Quelle grandeur caractéristique du circuit (E ou R) le professeur a-t-il changée pour obtenir la courbe n°1? Justifier. L'inductance et la résistance de la bobine sont inchangées : la constante de temps augmente. Or t = (R+r) / L ; donc la résistance R a augmenté. Ce qui est confirmé par la diminution de l'intensité en régime permanent ( E étant restée constante).

retour -menu