|
Champ magnétique crée par une bobine, radioactivité naturelle du bismuth ( bac Stl biologie, génie biologique 2009) |
|||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||
|
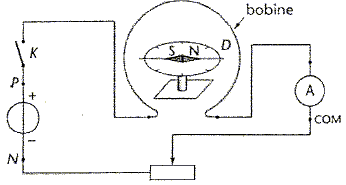
la boussole des tangentes est un dispositif constitué d'une bobine plate verticale, comportant N spires de rayon R, au centre de laquelle est placée une aiguille aimantée mobile dans un plan horizontal. On réalise le montage ci-dessous :
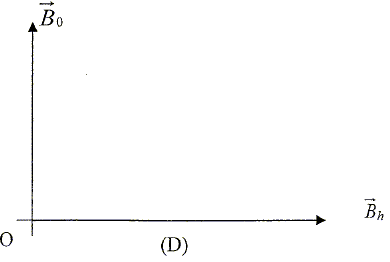
Lorsque le circuit est ouvert, l'aiguille de la boussole est orientée selon la composante horizontale Bh du champ magnétique terrestre ( on appelle D cette direction ). On oriente la bobine de telle sorte que son plan contienne D. Lorsque le circuit est fermé, la bobine parcourue par un courant crée en son centre O un champ magnétique B0 tel que représenté sur le schéma suivant :
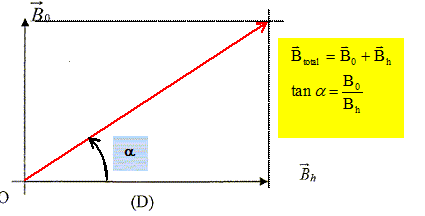
L'aiguille tourne alors d'un angle a par rapport à la direction D. Schématisation du champ magnétique résultant. Reproduire le schéma ci-dessus et construire le vecteur représentant le champ magnétique Btotal selon lequel s'oriente l'aiguille aimantée lorsque le circuit est fermé. Faire figurer l'angle a. Ecrire l'expression vectorielle du champ magnétique résultant. Donner une relation entre a, B0 et Bh.
On fait varier l'intensité I
du courant dans la bobine et on mesure la déviation
a
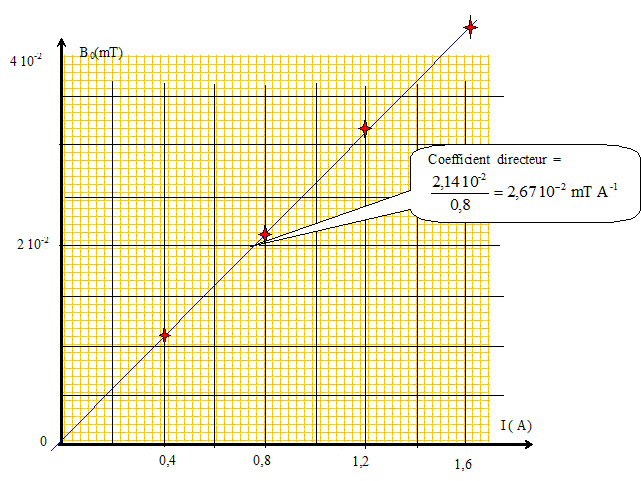
de l'aiguille aimantée. Bh = B0 / tan a = constante. = 1,994 10-2 = 2,00 10-2 = 2,00 10-2 Tracer le graphique représentant l'évolution de B0 en fonction de l'intensité I. Montrer à l'aide du graphique que B0 est proportionnel à I.
Le graphe est une droite passant par l'origine : B0 et I sont donc proportionnels. La bobine étudiée comporte N spires de rayon R = 7,0 cm. L'expression de B0 est B0 = µ0N I / (2R) avec µ0 = 4 pi 10-7 SI. En déduire la valeur de N. µ0N / (2R) = 2,67 10-2 mT A-1 = 2,67 10-5 T A-1 ; N = 2,67 10-5 *2R / µ0 = 2,67 10-5 *0,14 /(4*3,14 10-7) = 3 spires.
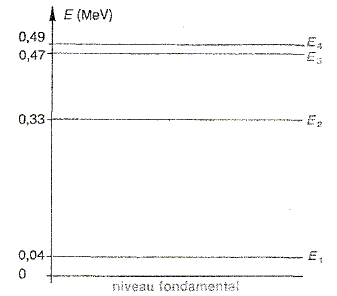
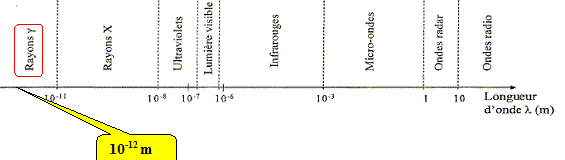
radioactivité naturelle du bismuth. En dehors de l'isotope 209 du bismuth, on connaît 32 autres isotopes du bismuth, ayant des "durées de vie" comprises entre 50 µs et 3 millions d'années. Etude de quelques isotopes du bismuth. Définir le mot "isotope". Des isotopes ont le même nombre de charge Z, mais des nombres de neutrons différents. Donner la composition du noyau de bismuth 20983Bi. 83 protons et 209-83 =126 neutrons. Le bismuth 209 se désintègre par radioactivité en produisant un noyau fils de thallium 205, tandis que que l'isotope 207 subit une désintégration b+. Ecrire la réaction de désintégration de chacun des deux isotopes en précisant les lois utilisées et en identifiant les particules et noyau fils émis. Indiquer le type de radioactivité de l'isotope 209. On donne : thalium 81Tl ; plomb 82Pb ; bismuth 83Bi ; polonium 84Po ; astate 85At. 20983Bi --->20581Tl + AZX. Conservation de la charge : 83 = 81 + Z d'où Z = 2 : élément hélium He ( type de radioactivité a ) Conservation du nombre de nucléons : 209 = 205 +A d'où A = 4. 20983Bi --->20581Tl + 42He. 20783Bi --->A'Z'X' + 01e ( positon) Conservation de la charge : 83 = Z' +1 d'où Z' = 82 ( élément plomb Pb ) Conservation du nombre de nucléons : 207 = A' +0 20783Bi --->20782Pb + 01e. La demi-vie ( période radioactive) du bismuth 210 est T = 5,0 jours. Un échantillon contient initialement une masse m = 1,0 10-2 g de bismuth 210. Définir la demi-vie radioactive. Durée au bout de laquelle la moitié des noyaux initiaux se sont désintégrés ; durée au bout de laquelle l'activité initiale est divisée par deux. Calculer, en détaillant les calculs, la valeur de la masse m' de bismuth 210 restant. Loi de décroissance radioactive : m(t) = m(t=0) exp ( -lt) avec l = ln2 / T = ln2 / 5,0 = 0,1386 jour-1. m' =m exp(-0,1386*10) = 0,25 m = 0,25 *1,0 10-2 = 2,5 10-3 g.
|
|||||||||||||||||||||||||||||||||||||||||||
|
|