Elément cadmium : complexation de l'ion cadmium (II) ; autour du chlorure de plomb, ( bac Stl chimie de laboratoire 2009)

Classification périodique et radioactivité. Données à 25 °C : - constante de dissociation du complexe [Cd(CN)4]2- : KD = 1,6 10-19 ; - potentiel standard E°(Cd2+(aq) / Cd(s) = -0,40 V. palladium 46Pd ; argent 47Ag ; cadmium 48Cd ; indium 49In. Donner la structure électronique de l'atome de cadmium dans son état fondamental. 1s2 2s2 2p6 3s2 3p6 4s2 3d10 4p6 5s2 4d10 Donner, en justifiant, la structure électronique de l'atome qui se trouve dans la même colonne que le cadmium mais dans la ligne au-dessus. Lés éléments d'une même colonne ( famille) ont la même structure électronique externe. Elément Zinc : 1s2 2s2 2p6 3s2 3p6 4s2 3d10 Donner la structure électronique de l'ion cadmium Cd2+ dans son état fondamental. 1s2 2s2 2p6 3s2 3p6 4s2 3d10 4p6 4d10 L'un des isotopes du cadmium est obtenu lors de la réaction de désintégration de type b- de l'isotope 108 d'un élément radioactif X. Définir les termes radioactif et isotopes. Isotopes : des noyaux isotopes ont le même nombre de charge Z mais des nombres de nucléons A différents. Un noyau radioactif est un noyau instable dont la désintégration (destruction) aléatoire s'accompagne : L'apparition d'un nouveau noyau L'émission d'une particule notée a, b - ou b + L'émission d'un rayonnement électromagnétique noté g. Définir l'émission b -. Un noyau émet un électron noté : -10e ; un neutron du noyau se transforme en proton Les particules b - sont assez peu pénétrantes. Elles sont arrêtées par quelques millimètres d'aluminium Ecrire l'équation de la réaction de désintégration radioactive en rappelant les lois utilisées et en identifiant X.     108ZX ---> A48Cd + -10e. Conservation du nombre de nucléons : 108 = A+ 0 ; A = 108. Conservation de la charge : Z = 48 -1 ; Z = 47. 10847Ag ---> 10848Cd + -10e. L'isotope 108 de X peut aussi subir une raction de désintégration de type b+. Ecrire l'équation de cette désintégration radioactive. 10849In ---> 10848Cd + +10e. Complexation des ions cadmium (II). A 100 mL d'une solution de nitrate de cadmium (II), Cd(NO3)2, de concentration égale à 1,0 10-3 mol/L, on ajoute 100 mL d'une solution de cyanure de potassium, KCN à 1,0 10-2 mol/L. Il se forme le complexe [Cd(CN)4]2-. Ecrire l'équation de la réaction qui se produit. Exprimer et calculer la constante de cette réaction ; que peut-on déduire de ce résultat ? Cd2+(aq) + 4 CN-(aq) = [Cd(CN)4]2-(aq). KF = [[Cd(CN)4]2-(aq)] / ( [Cd2+(aq)] [CN-(aq)]4 ) = 1/KD = 1 / 1,6 10-19 = 6,25 1018~6,3 1018. KF est très grande ; la réaction est totale ; le complexe est très stable. Calculer les concentrations, à l'équilibre, de toutes les espèces intervenant dans la réaction. avancement (mol) Cd2+(aq) + 4 CN-(aq) = [Cd(CN)4]2-(aq) initial 0 0,10 * 1,0 10-3 = 1,0 10-4 0,10 * 1,0 10-2 = 1,0 10-3 0 en cours x 1,0 10-4 -x 1,0 10-3 - 4x x à l'équilibre xéq 1,0 10-4 -xéq 1,0 10-3 - 4xéq xéq La réaction étant totale : 1,0 10-4 -xéq ~ 0 ; xéq ~ 1,0 10-4 mol [[Cd(CN)4]2-(aq)] = xéq / 0,20 = 5 xéq = 5,0 10-4 mol/L. [CN-(aq)] = (1,0 10-3 - 4xéq ) / 0,20 = 5* (1,0 10-3 - 4xéq ) = 5 ( 1,0 10-3 - 4,0 10-4 ) =3,0 10-3 mol/L. [Cd2+(aq)] = [[Cd(CN)4]2-(aq)] / (KF [CN-(aq)]4) = 5,10-4 / (6,25 1018*(3,0 10-3)4 ) =9,88 10-13 ~ 9,9 10-13 mol/L. 6,25 1018 (1,0 10-4 -xéq)54 *(1,0 10-3 - 4xéq )4 = xéq. Exprimer puis calculer le potentiel redox indiqué par une électrode de cadmium plongeant dans le mélange. Cd(s) +4 CN-(aq) = 2e- + [Cd(CN)4]2-(aq) E = E°( [Cd(CN)4]2-(aq) / Cd(s) + 0,06 / 2 log ( [[Cd(CN)4]2-(aq)] /[CN-(aq)]4 ). Cd(s) = 2e- + Cd2+(aq) ; E = E°(Cd2+(aq) / Cd(s) ) + 0,06 / 2 log [Cd2+(aq)] Or [Cd2+(aq)] = [[Cd(CN)4]2-(aq)] / (KF [CN-(aq)]4) d'où : E = E°(Cd2+(aq) / Cd(s) ) + 0,06 / 2 log ( [[Cd(CN)4]2-(aq)] / (KF [CN-(aq)]4) ) E = E°(Cd2+(aq) / Cd(s) ) + 0,03 log (1/KF) + 0,03 log ( [[Cd(CN)4]2-(aq)] /[CN-(aq)]4 ). E = -,040 - 0,03 log 6,25 1018 + 0,03 log ( 5,0 10-4 / (3,0 10-3)4 ) = -0,76 V. Ou plus simplement : E = E°(Cd2+(aq) / Cd(s) ) + 0,06 / 2 log [Cd2+(aq)] = -0,40 + 0,03 log (9,88 10-13) = -0,76 V. 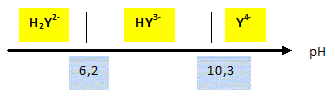Autour du chlorure de plomb. Données à 25 °C : - produit de solubilité du chlorure de plomb PbCl2 : Ks = 1,6 10-5 ; produit ionique de l'eau : Ke = 1,0 10-14 ; - constantes d'acidité de l'acide éthylènediaminetétracétique ( EDTA ): couple H4Y /H3Y- H3Y- / H2Y2- H2Y2- / HY3- HY3- /Y4- pKa1 = 2,0 pKa2 = 2,7 pKa3 = 6,2 pKa4 = 10,3 - M(PbCl2) = 278,1 g/mol ; - conductivité molaire ionique (l° ) à dilution infinie, en mS m2 mol-1 : l°(½Pb2+) = 7,1 ou l°(Pb2+) =14,2 ; l°(Cl-) = 7,6. Solubilité. Le chlorure de plomb est un composé peu soluble dans l'eau. Déterminer la solubilité, en mol/L, du chlorure de plomb dans l'eau. PbCl2(s) = Pb2+(aq) + 2 Cl-(aq) ; Ks = [Pb2+(aq)][Pb2+(aq)]2. La solution reste électriquement neutre : 2 [Pb2+(aq)] = [Cl-(aq)] Ks = [Pb2+(aq)] *(2 [Pb2+(aq)])2 = 4 [Pb2+(aq)]3 = 1,6 10-5. [Pb2+(aq)] = (4 10-6)1/3 =1,587 10-2 ~ 1,6 10-2 mol/L. On lave 100 g d'un précipité de chlorure de plomb avec 200 mL d'eau : on récupère une solution A ( filtrat ). Déterminer la masse de précipité dissoute dans A lors de ce lavage ainsi que la concentration en ion Pb2+ et Cl- dans la solution A. Quantité de matière (mol) de solide dissout dans 0,20 L d'eau : n = 0,20 * 1,587 10-2 =3,174 10-3 mol. Masse de solide dissoute : m = n . M(PbCl2) = 3,174 10-3 *278,1 = 0,88 g. [Pb2+(aq)] =1,6 10-2 mol/L ; [Cl-(aq)] = 2 [Pb2+(aq)] = 2*1,587 10-2 ~ 3,2 10-2 mol/L. La masse dissoute serait-elle plus importante si le précipité était lavé avec une solution de chlorure de sodium ? Justifier sans calcul. En présence d'un ion commun, ici l'ion chlorure, la solubilité du chlorure de plomb diminue : la masse dissoute sera donc plus petite.   Etude de la conductivité de la solution A. On cherche à vérifier la concentration en ion Pb2+ et Cl- dans la solution A ; à cet effet, on mesure , à 25°C, la conductivité s de cette solution : elle vaut 467 mS m-1. Donner la relation perettant de calculer la conductivité de la solution A. Préciser les unités des grandeurs utilisées dans la relation. s = l°(Pb2+) [Pb2+] + l°(Cl-) [Cl-]. avec [Pb2+] et [Cl-] en mol m-3 ; s en mS m-1 ; l°(Pb2+) et l°(Cl-) en mS m2 mol-1. Exprimer cette conductivité uniquement en fonction de la concentration C en ion Pb2+. [Cl-] = 2 [Pb2+] = 2 C d'où : s = l°(Pb2+) C + l°(Cl-) 2C. s = (l°(Pb2+) + 2l°(Cl-) ) C. Déterminer la concentration C et érifier que cette valeur est bien compatible avec le résultat ci-dessus. C = s / (l°(Pb2+) + 2l°(Cl-)) =467 / (14,2 + 2*7,6) =15,67 mol m-3 =15,67 / 1000 mol L-1 ~ 1,6 10-2 mol /L. Les deux résultats sont bien compatibles. Dosage complexométrique des ions Pb2+ par l'EDTA. On dose un volume VA = 10 mL de la solution A par l'EDTA, Y4 à la concentration CEDTA = 2,0 10-2 mol/L ; il se forme le complexe PbY2-. ce dosage est réalisé en milieu tamponé à pH = 5,0, en présence d'un indicateur coloré convenable. Donner le diagrmme de prédominance des espèces issues de l'EDTA dans un domaine compris entre 4,0 et 14.  En déduire la forme prédominante de l'EDTA à pH = 5,0. à pH compris entre pKa2 et pKa3, a forme H2Y2- prédomine à pH = 5,0. Ecrire l'équation de la réaction de dosage supposée quantitative. Pb2+ (aq) + H2Y2-(aq) = PbY2- (aq) + 2H+(aq). L'équivalence est obtenue pour un volume VE = 8,00 mL de la solution d'EDTA. Vérifier que la concentration en ion Pb2+ dans la solution A est bien celle trouvée précédemment. A l'équivalence, les quantités de matière des réactifs mis en présence sont en proportions stoechiométriques. VE CEDTA = [Pb2+] VA ; [Pb2+] = VE CEDTA / VA =8,00 * 2,0 10-2 / 10 = 1,6 10-2 mol/L.

retour -menu