Chimie : argenture, potentiométrie, radioactivité 110Ag ( bac Stl physique de laboratoire 2009)

L'élément chimique argent ( Ag ) permet différentes utilisations ( argenture d'objets, piles, etc...) dont on étudiera certaines. Données : M(Ag) = 107,8 g/mol ; m(AgCN) = 133,8 g/mol. Formule de l'ion cyanure CN- ; on suppose que cet ion n'intervient pas dans les réactions. Loi de décroissance radioactive N(t) = N0 exp(-lt ) : nombre de noyaux radioactifs à l'instant t. Activité d'une source radioactive : A(t) = A0 exp(-lt ). Extrait de la classification périodique : 43Tc, 44Ru, 45Rh, 46Pd, 47Ag, 48Cd, 49In, 50Sn, 51Sb. L'argenture. L'argenture est une activité de l'orfèvrerie qui consiste, par le passage d'un courant électrique dans une solution aqueuse ionique ( électrolyte), à déposer une couche de métal argent sur un objet, lui donnant une belle surface brillante. Le bain est une solution ionique de cyanure d'argent contenant les ions Ag+ et CN-. La solution est préparée à partir d'un solide AgCN mis en solution dans un volume d'eau pure. Pour une bonne qualité d'argenture, le bain doit avoir une concentration minimale en ion argent de 0,25 mol/L. Préparation du bain électrolytique : sachant que la solution doit présenter une concentration massique Cm d'environ 40 g/L de cyanure d'argent, déterminer le volume d'eau V nécessaire pour dissoudre tout le contenu d'une boîte de 250 g du solide AgCN. V = 250/Cm = 250/40 = 6,25 ~ 6,3 L. Ecrire l'équation de dissolution de AgCN dans l'eau. AgCN(s) ---> Ag+ (aq) + CN- (aq). Exprimer en fonction de Cm et de la masse molaire M(AgCN), la concentration molaire c en soluté apporté puis la calculer. c = Cm / M(AgCN) = 40 / 133,8 = 0,299 ~0,30 mol/L. En déduire la concentration [Ag+]0 des ions argent présents dans la solution de départ. [Ag+]0 = c = 0,30 mol/L. 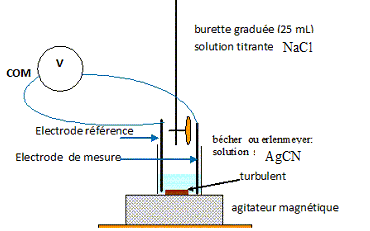Une fourchette ainsi argentée a une masse d'argent déposée md = 4,0 g ; calculer la quantité de matière nAg correspondant à ce dépôt de métal argent. nAg = md / M(Ag) = 4,0 / 107,8 = 3,71 10-2 ~3,7 10-2 mol. Le passage de l'ion argent au métal est-il une oxydation ou une réduction ? Justifier. L'ion argent gagne un électron : Ag+ (aq)+ e- = Ag(s). L'ion argent est un oxydant qui se réduit : réduction de l'ion argent. Pour contrôler la concentration des ions argent d'un bain électrolytique, noté S, on procède à un dosage potentiométrique. On prélève V = 5 mL de la solution S, que l'on dilue 10 fois. Puis on dose un volume V1 = 25 mL de cette solution diluée S1. On réalise le dosage avec une solution titrante de chlorure de sodium ( Na+ + Cl- ) de concentration c = 1,0 10-1 mol/L. Faire un schéma annoté du dosage potentiométrique réalisé.     Donner l'équation de la réaction ayant lieu au cours de ce dosage. Ag+(aq) + Cl-(aq) = AgCl(s). Sachant que le volume de la solution titrante à l'équivalence est Véq = 7,0 mL, exprimer la concentration [Ag+]f de la solution diluée dosée en fonction de Véq, c et V1. Calculer sa valeur. A l'équivalence, les quantités de matière des réactifs mis en présence sont en proportions stoechiométriques. [Ag+]f V1 = Véqc ; [Ag+]f = Véqc / V1. [Ag+]f =7,0*0,10 / 25 =2,8 10-2 mol/L. Exprimer la concentration [Ag+] de la solution S du bain d'argenture en fonction de [Ag+]f et calculer sa valeur. La solution S a été diluée 10 fois : [Ag+] = 10 [Ag+]f = 10*2,8 10-2 =0,28 mol/L. Cette concentration est-elle suffisante pour continuer l'opération d'électrolyse ? "Pour une bonne qualité d'argenture, le bain doit avoir une concentration minimale en ion argent de 0,25 mol/L" On peut donc continuer l'électrolyse ( 0,28 > 0,25).   Radioactivité. L'argent de numéro atomique Z = 47, présente deux isotopes : 107Ag et 110Ag. Donner la composition du noyau de l'isotope 110. 47 protons et 110-47 =63 neutrons. L'isotope 110Ag présente les propriétés suivantes : période radioactive T = 249 jours ; activité pour 1,0 g : A0 = 1,76 1014 Bq ; émetteur b-. Ecrire l'équation correspondante à la désintégration de cet isotope en précisant les lois utilisées. 11047Ag ---> AZX + 0-1e. Conservation de la charge : 47 = Z-1 d'où Z = 48 ; on identifie l'élément 48Cd Conservation du nombre de nucléons : 110 = A + 0. 11047Ag ---> 11048Cd + 0-1e. En utilisant la loi de décroissance radioactive, montrer que la constante radioactive peut se mettre sous la forme l = ln 2 / T. Calculer l en j-1. N(t) = N0 exp(-lt ) ; N(T) = ½N0 = N0 exp(-lT) ½ = exp(-lT) ; ln ½ = -lT ; ln½ = -ln 2 ; par suite : lT = ln 2. T = ln 2 /T = ln 2 / 249 = 2,78 10-3 j-1. Combien de temps t faut-il à 1,0 g de cet isotope pour que son activité devienne égale à 4,4 1013 Bq ? A(t) = A0 exp(-lt ) ; A(t) / A0 = exp(-lt ) ; ln (A(t) / A0) = -lt ln (A0 /A(t) ) = lt ; t = ln (A0 /A(t) ) / l. t = ln ( 1,76 1014 / 4,4 1013) / 2,78 10-3 = 499 jours ~ 5,0 102 jours.

retour -menu