Installation électrique triphasée, moteur asynchrone, compresseur ( bac STI génie civil, énergétique 2009)

L'entreprise est alimentée par un réseau triphasé 230 V / 400 V ; 50 Hz. L'installation, supposée équilibrée, consomme en moyenne par mois ( durée de fonctionnement Dtf = 176 heures ) une énergie active Wa = 11,8 MWh et une énergie réactive Wr = 7,0 MVAh. Calculer les valeurs moyennes : - des puissances active P et réactive Q consommées par l'installation. Diviser l'énergie exprimée en kWh par la durée moyenne exprimée en heure : ( M : 1 méga = 1 103 kilo ) P = Wa /Dtf = 11,8 103 / 176 = 67,0 kW. Q = Wr /Dtf = 7,0 103 / 176 =39,77 ~ 39,8 kvar. - de la puissance apparente S de l'installation : S2 = P2 + Q2 = 67,02 + 39,772 = 6073 ; prendre la racine carrée : S = 6073½ = 77,9 kVA. - du facteur de puisance k de l'installation : k = P/S = 67 / 77,9 = 0,86. - de l'intensité efficace I du courant en ligne : S = 3½ U I ; I =S / (3½U) = 77,9 103 / ( (3½*400) = 112,4 ~ 112 A. Afin de limiter la puissance apparente souscrite auprès du fournisseur d'électricité à S' = 70 kVA, on envisage de brancher à l'entrée de l'installation une batterie de condensateurs. Calculer la nouvelle puisance réactive Q' de l'installation. Les condensateurs ne consomment pas de puissance active : P reste donc inchangée. S'2 = P2 + Q'2 ; Q'2 = S'2 - P2. Q'2 =702 - 672 = 411 Prendre la racine carrée : Q' = 411½ =20,27 ~ 20,3 kvar. En déduire la puissance réactive QC que devra fournir la batterie de condensateurs. Les puissances réactives s'ajoutent : Q + QC = Q' ; QC = Q' -Q = 20,3-39,8 = -19,5 kvar. Quelles conséquences cela entraîne t-il sur le facteur de puissance ainsi que sur l'intensité en ligne ? k = P / S' ; P inchangée et S' diminue, donc k augmente. I = S' / (3½ U) ; U inchangé et S' diminue, donc I diminue. 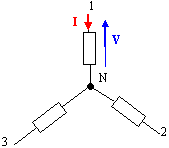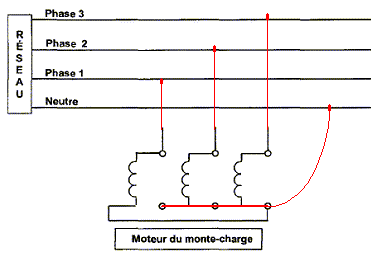Moteur asynchrone triphasé d'un monte-charge. Accélération de la pesanteur g = 10 m s-2. En fonctionnement nominal, le monte charge élève à vitesse constante, une charge de masse m = 1500 kg à une hauteur H = 5 m en une durée Dt = 25 s. Calculer le travail W effectué par la force motrice s'exerçant sur la charge. W = mgH =1500*10*5 =7,5 104 J = 75 kJ. Calculer la puissance mécanique utile Pu que développe le moteur ( rendement mécanique hm = 75 % ). Pu = W / (Dt hm ) = 75 /(25*0,75) = 4,0 kW. Le moteur asynchrone triphasé présente la plaque signalétique suivante : 230 V / 400 V ; 50 Hz ; triangle 14,4 A et étoile 8,3 A ; 4 kW ; 1440 tr/min ; cos j = 0,83. Vérifier que la puissance utile nominale Pun de ce moteur est bien adaptée au monte-charge. La plaque signalétique indique Pun = 4 kW, valeur égale à la puissance mécanique utile. Ce moteur est donc bien adapté au monte-charge. Préciser en le justifiant le couplage des enroulements du stator de ce moteur. P = 3½U I cos j ; I = P / (3½ U cos j) = 4000 / (1,732*400*0,83) ~ 7 A. Le constructeur indique une intensité en ligne de 8,3 A pour un couplage étoile . La tension maximale que peut supporter un enroulement correspond à la plus petite des tensions indiquées sur la plaque signalétique soit 230 V. Dans le couplage étoile, la tension aux bornes de chaque enroulement est égal à la tension simple 230 V et chaque enroulement est traversé par l'intensité en ligne. Faire apparaître ce couplage et les connexions du moteur avec le réseau.   Calculer le moment du couple utile nominale Tun du moteur. 1440 tr/min ou 1440 / 60 = 24 tr /s 1 tour correspond à 2 pi radians ; la vitesse angulaire du moteur vaut : w= 24*2 pi = 24*6,28 = 150,8 rad/s. Tun = Pun / w=4000 / 150,8 = 26,5 Nm. ou bien : Putile / (2pi n) avec n =1440/60=24 tr/s Déterminer la vitesse nS de synchronisme en tr / min et le nombre p de paires de pôles du moteur.  nS= vitesse de rotation (tr/s) / nombre de paires de pôles avec f = 50 Hz nS =50 /p tr/s ou 50*60 / p = 3000 / p tr/min. Or la vitesse de rotation du moteur ( 1440 tr/min) est très proche de la vitesse de synchronisme : d'où nS = 1500 tr/min et p = 2. Calculer le glissement nominal gn du moteur. glissement gn = (nS-n)/nS = (1500-1440)/1500 = 0,04 ( 4%). Calculer la puissance nominale Pan absorbée par le moteur et le rendement nominal hn de celui-ci. puissance absorbée par ce moteur : Pan = 3½U Icosj =3½*400*8,3*0,83 = 4,77 kW. rendement de ce moteur : hn = Pun / Pan=4 / 4,77 = 0,84 ou 84%. En déduire le rendement global du monte-charge. hn *hm =0,84*0,75 = 0,63 ou 63 %.   Etude du compresseur. Le compresseur est actionné par un moteur thermique. On donne : R = 8,31 J mol-1 K-1. Masse volumique du gazol r = 860 kg m-3 ; g = 10 m s-2 et 1 bar = 105 Pa. Le compresseur envoie de l'air comprimé, sous une pression p = 7 bar à une température q = 45 °C, dans une cuve de stockage de volume V = 300 L. En considèrant l'air comme un gaz parfait, calculer le nombre n de moles d'air dans la cuve. PV = nRT ; n = PV / (RT). P = 7 105 Pa ; V = 0,3 m3 ; T = q +273 = 45+273 =318 K. n = 7 105 *0,3 / (8,31*318) =79,47 ~79,5 mol. Déterminer le volume V' qu'occuperait l'air stocké dans lacuve à une température q'=18°C et sous une pression de 1 bar. V' = nRT' / P = 79,47 *8,31*(273+18) / 105 = 1,92 m3. Le gazol, qui sert à alimenter le moteur du compresseur est contenu dans un réservoir. La hauteur du liquide dans celui-ci est h = 1,60 m. le réservoir est muni à sa base d'une vanne de diamètre D = 6 cm. La surface libre du gazol est à la pression atmosphérique patm = 1 bar. Calculer la différence de pression Dp entre un point situé à la surface libre du gazol et un point situé au niveau de la vanne. Dp = rg(h -½D)= 860*10*(1,6-0,03) = 1,35 104 Pa = 0,135 bar ( au centre de la vanne). En déduire la pression absolue pv au niveau de la vanne. pv = Dp + patm =1,35 104 + 105 = 1,135 105 Pa = 1,135 bar. Calculer l'intensité de la force pressante F exercée par le gazol sur la vanne. Comparer cette valeur à la valeur maximale préconisée par le constructeur, Fm = 1,7 kN. F = pv S avec S section de la vanne. S = pi D2/4 = 3,14 * 0,062/4 =2,826 10-3 m2. F = 1,135 105 *2,826 10-3 = 321 N = 0,32 kN. Valeur inférieure à Fm, les conditions de sécurité sont donc respectées.

retour -menu