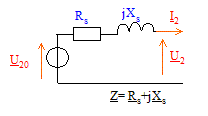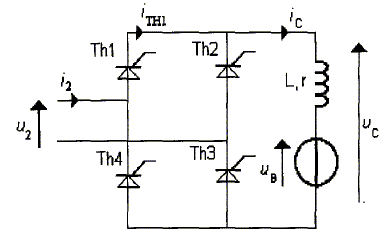
Chargeur de batterie : transformateur, pont tout thyristor ( bac STI électrotechnique 2009)

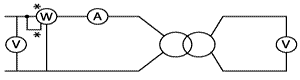
Le chargeur de batterie intègre un transformateur monophasé et un pont tout thyristor. Le transformateur monophasé seul : étude en régime sinusoïdal. Essai à vide sous tension primaire nominale : Les résultats de cet essai sont les suivants : tension efficace primaire nominale: U1N = 230 V ; tension efficace secondaire à vide U2V = 27 V ; intensité efficace au primaire à vide I1V = 600 mA ; puissance primaire à vide P1V = 30 W. Proposer un schéma de cçablage permettant de réaliser les mesures de cet essai. préciser le mode d'utilisation ( AC ou DC ) des appareils de mesures quand cela est nécessaire. Voltmètre et ampèremètres sont utilisés en mode AC. Il convient de brancher les appareils en longue dérivation, car à vide le courant est faible et la tension est nominale. Calculer le rapport m de transformation. m = U2V / U1N = 27/230 = 0,1174 ~ 0,117. Justifier que P1V la puissance primaire à vide, correspond, à peu de chose près, aux pertes magnétiques à vide PFV. On donne la valeur de la résistance de l'enroulement primaire r1 = 1 W. Lors de l'essai à vide on mesure les pertes Joule à vide et les pertes fer PFV=30 W ; les pertes Joule valent : r1 I21V =1*0,62 =0,36 W, soit 0,36*100/30 ~ 1,2% des pertes totales du transformateur lors de cet essai. On peut donc les négliger. On considère donc PFV = P1V = 30 W. Essai en court-circuit avec intensité secondaire nominale :   Les résultats de cet essai sont les suivants : tension efficace réduite au primaire : U1CC = 25 V ; intensité efficace du courant au secondaire I2CC = I2N = 20 A ; puissance primaire en court-circuit P1CC = 40 W. Expliquer pourquoi la tension au primaire n'est pas nominale lors de cet essai. L'intensité du courant débité par le secondaire n'est limitée que par l'impédance du secondaire ; or celle-ci étant très faifle, l'intensité sera très élevée. Pour avoir l'intensité efficace nominal au secondaire, la tension primaire doit être réduite au primaire. Justifier que P1CC, la puissance primaire en court-circuit, correspond, à peu de chose près, aux pertes PJCC par effet Joule en court-circuit. Par hypothèse : Pfer = kU²1. PferV / U²1V = PferCC / U²1CC = k soit PferCC= PferVU²1CC / U²1V = 30*25²/230² = 0,35 W. or PferCC/ P1CC = 0,35/ 40 *100= 0,88%.  Les pertes fer sont négligeables lors de l'essai en court circuit. P1CC =  PferCC+ PJCC =40 W on en déduit : PJCC =40 W. Modèle équivalent : Représenter le modèle équivalent du transformateur vu du secondaire. modèle de Thévenin vu du secondaire (secondaire à vide) : Les grandeurs soulignées sont des nombres complexes. Déterminer les valeurs numériques des éléments RS et XS de ce modèle. A l'aide de l'essai en court-circuit, calcul de la résistance Rs et la réactance Xs des enroulements ramenées au secondaire : Rs = P1cc / I²2cc =40/202 = 0,1 W. or Z = m U1cc / I2cc =0,1174*25/20 = 0,14675 W. de plus : Z²=Rs² + Xs² d'où Xs² = Z²-Rs² = 0,0,14675²-0,1² = 0,01154 ; Xs =0,107 ~ 0,11 W. Prédétermination du rendement. A partir du modèle équivalent du transformateur, des essais à vide et en court-circuit, on souhaite prédéterminer le rendement du transformateur. On se place dans le cas où il fonctionne sous tension primaire nominale et il alimente une charge inductive de facteur de puissance cos j2 =0,8, parcourue par un courant d'intensité efficace I2=I2N=20 A. Déterminer la valeur approchée de la chute de tension DU2 au secondaire sachant qu'elle a pourexpression : DU2 ~ RS I2N cos j2 + XS I2N sin j2 . sin j2 =0,6 ; DU2 ~0,1*20*0,8 +0,107 *20*0,6 =2,884 V~ 2,88 V. Exprimer puis calculer la puissance active secondaire nominale P2. P2 = U2N I2N cos j2 = 27 * 20 * 0,8 = 432 W. En justifiant, donner les valeurs des pertes magnétiques PF et des pertes Joule PJ prévisibles pour ce fonctionnement. Les pertes fer sont proportionnelles au carré de la tension nominale primaire. Or à vide comme en charge, la tension au primaire est nominal, les pertes fer sont donc les mêmes soit PF = 30 W. Les pertes Joule sont proportionnelles au carré de l'intensité nominale secondaire. Or à vide comme en charge, l'intensité secondaire est nominale : PJ = 40 W. Déterminer le rendement h du transformateur pour ce fonctionnement. h = P2 / (P2+PJ+PF) = 432 / (432+40+30) =0,86 (86 %). Le pont tout thyristor :  Le pont tout thyristor est alimenté sous une tension u2 telle que u2 = 24* 2½ sin (100 pi t). Il alimente la batterie du scooter électrique ( dont la résistance interne est négligeable ) mise en série avec une bobine de forte inductance et de résistance interne r négligeable. Cette charge ainsi constituée est parcourue par un courant d'intensité iC~ 20 A. La commande des thyristors, supposés parfaits, est conçue pour que : Th1 et Th3 soient commandés à la date t0 sur l'intervalle ]0 ; T[ ; Th2 et Th4 soient commandés à la date t0+½T sur l'intervalle ]0 ; T[. Le retard à l'amorçage t0 est égal à 3,0 ms. Préciser le rôle de la bobine. La bobine lisse l'intensité du courant afin que celui-ci se rapproche le plus possible d'un courant continu. Compléter le tableau suivant en exprimant uC en fonction de u2 et en donnant les valeurs de I2 et iTh1 suivant les intervalles de conduction. intervalle de temps ]0 ; t0[ ]t0 ; ½T [ ]½T ; ½T +t0[ ]½T +t0 ; T[ Thyristors conducteurs Th2 et Th4 Th1 et Th3 Th1 et Th3 Th2 et Th4 uC -u2 u2 u2 -u2 I2 -20 20 20 -20 iTh1 0 20 20 0 Représenter les chronogrammes de uC, I2 et iTh1. 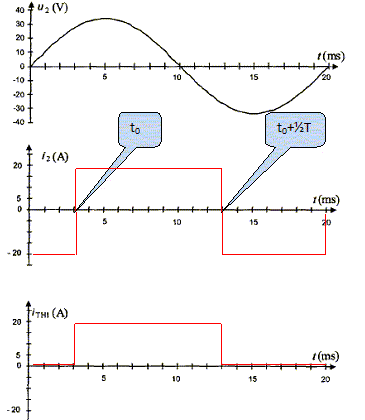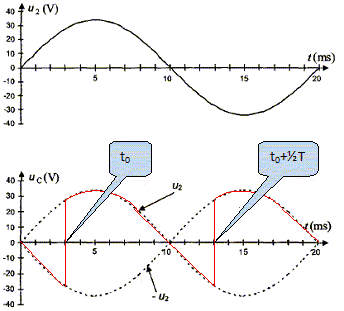Quelle est la fréquence de la tension uC ? période T = 10 ms = 0,010 s ; f = 1/T = 1/0,010 = 1,0 102 Hz.

retour -menu