Transformateur, redresseur, moteur à courant continu ( bac STI mécanique 2009)

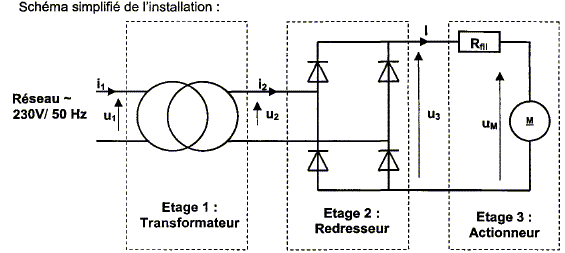
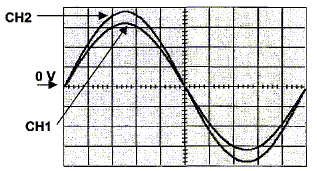
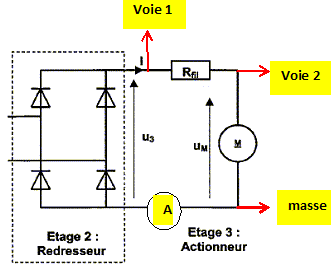
L'étude porte sur un système de store intérieur motorisé. Les étages 1 et 2 constituent le système d'alimentation du dispositif. Le transformateur est branché sur le réseau EDF ( 230 V / 50 Hz). L'étage 3 ( actionneur ) comporte le moteur qui permet de monter ou descendre le store. Le moteur est à courant continu à aimants permanents. Sa tension nominale est de 24 V. Rfil modèlise la résistance des fils situés entre le dispositif d'alimentation et le moteur. Partie 1 : étude du transformateur, étage 1. Le transformateur est supposé parfait. On a relevé l'oscillogramme des tensions u1 ( voie CH1) et u2 ( voie CH2) : CH1 : 100 V/div, couplage DC ; CH2 : 10 V/div, couplage DC. Base de temps : 2 ms / div Déterminer l'amplitude U2max de la tension u2. 3,8 div et 10 V par division soit 3,8*10 = 38 V. Déterminer la valeur efficace U2 de la tension u2. En déduire le rapport de transformation m. U2 = U2max / 1,414 = 38/1,414=26,9 V. m = U2/U1 = 26,9 / 230 = 0,117 ~ 0,12. Si la valeur efficace du courant i2 vaut I2 = 210 mA, quelle est la valeur efficace I1 du courant i1 ? I1 =m I2 = 0,117 *210 = 24,6 mA. Calculer la puissance apparente S du transformateur. S = U1I1 = U2I2 = 230 * 0,0246 = 5,65 ~ 5,7 W. Quel est le rôle du transformateur dans l'installation ? 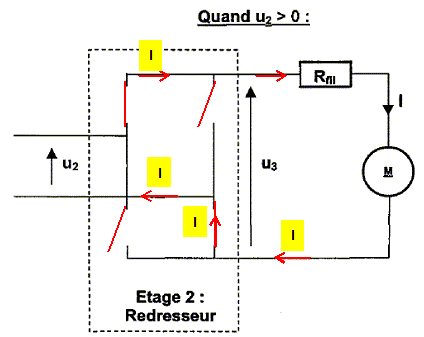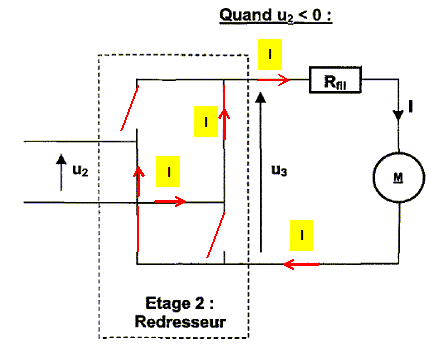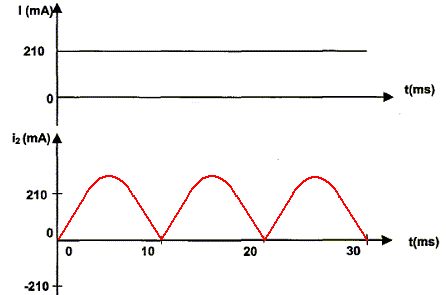La tension du secteur est abaissée à 24 V, valeur beaucoup moins dangereuse que 230 V : c'est une sécurité pour l'utilisateur. Partie 2 : étude du redresseur, étage 2. On suppose les diodes parfaites et le courant I constant, avec I = 210 mA. Compléter le document pour chaque phase de fonctionnement u2>0 et u2 <0. - en remplaçant chaque diode par un interrupteur ouvert ou fermé selon son état ( passante ou bloquée) - en fléchant le chemin emprunté par le courant I. On donne le chronogramme de la tension u2. 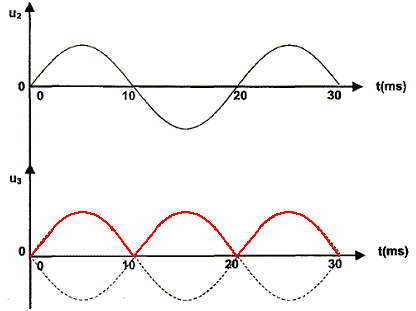Tracer le chronogramme de la tension u3. Déterminer la fréquence f de la tension u3. période T = 10 ms = 1,0 10-2 s. Fréquence f = 1/T = 1/ 1,0 10-2 = 100 Hz = 1,0 102 Hz. Déduire de ce qui précède le chronogramme du courant i2. Placer l'ampèremètre numérique permettant de mesurer la valeur efficace du courant I2, en précisant le mode de mesure utilisé ( AC, DC, AC+DC). Indiquer les branchements de l'oscilloscope permettant d'obtenir les oscillogrammes de u3 et uM. L'ampèremètre doit être utilisé sur la position AC pour lire la valeur efficace. Partie 3 : étude du moteur. 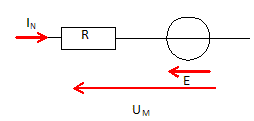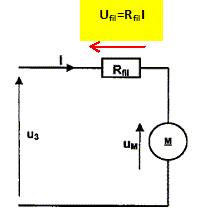Dans cette partie l'influence Rfil qui apparaît sur les différentes figures sera négligée. On appelle : Um = 24 V, tension d'alimentation ; E : force électromotrice induite ; R = 24 ohms, résistance interne du moteur ; I : courant induit ; IN = 210 mA et Tu = 0,94 N m. Pour fonctionner correctement le moteur doit être parcouru par un courant continu. On considère que ce moteur est alimenté sous sa tension nominale et qu'il fonctionne à couple constant nominal pendant la montée et la descente du store. Donner le schéma du modèle équivalent de Thévenin de l'induit du moteur. Pour un fonctionnement nominal : - calculer la puissance absorbée Pa. Pa= Um IN =24*0,21 = 5,04 ~ 5,0 W. - calculer la force électromotrice E. Um = E +R IN ; E = Um-RIN = 24-24*0,21 = 18,96 ~ 19 V. - calculer les pertes par effet Joule dans l'induit PJ. PJ = R I2N = 24*0,212 = 1,058 ~ 1,1 W. On considère que les pertes par effet Joule sont les seules pertes dans le moteur. En déduire la puissance utile Pu. Pu = Pa-PJ =5,04 - 1,058 = 3,982 ~ 4,0 W. Calculer le rendement du moteur h. h =Pu / Pa =3,982 / 5,04 =0,79 ( 79 %) Détection de fin de course : Lorsque le store arrive en butée ( fin de course en position haute ou basse), la rotation du moteur est bloquée, et le courant augmente. Un dispositif détecte alors l'augmentation du courant et coupe l'alimentation du moteur. Lorsque le moteur arrive en butée, que vaut la force électromotrice Eb ? Justifier. La rotation du moteur étant bloquée, la force électromotrice est nulle : Eb=0. Calculer la valeur du courant Ib en butée. Um = Eb +R Ib ; Ib =Um/R = 24/24 = 1,0 A. Partie 4 : étude de la chute de tension dans les câbles. Selon les installations, le dispositif d'alimentation peut être plus ou moins éloigné du moteur. La résistance des câbles électriques reliant le moteur à l'alimentation est d'autant plus grande que la section est petite. Ceci implique que la résistance des câbles n'est pas négligeable pour étudier le fonctionnement de l'installation, et que l'installateur doit en tenir compte. On a dessiné le schéma électrique de l'étage actionneur. On rappelle que Rfil modèlise la résistance des fils situés entre le dispositif d'alimentation et le moteur. Flècher la tension aux bornes de la résistance Rfil en convention récepteur. Ecriver la loi des mailles sur les tensions instantanées. u3 = Rfil i + uM. En déduire que : <uM> = <u3>-Rfil I. uM=u3 - Rfil i soit : <uM> = <u3>-Rfil <i >. Or I est un courant continu I=<i> ; <uM> = <u3>-Rfil I. Quelle est l'influence de la résistance des fils sur la vitesse de rotation du moteur ? Lorsque la résistance des fils augmente, la tension <uM> aux bornes du moteur diminue ; en conséquence le moteur tourne moins vite. On donne <u3> = 24 V et Imax = 1 A le courant maximal appelé par le moteur. Le fil utilisé a une longueur totale L = 100 m. La résistance du fil par unité de longueur est de 0,045 ohm m-1. Déterminer <uM> et conclure sachant que le fabriquant préconise une tension moyenne d'alimentation au moins égale à 20 V. Rfil = 0,045*100 = 4,5 ohms. <uM> = <u3>-Rfil Imax = 24 - 4,5 * 1 =19,5 V. Dans le cas d'une intensité atteignant 1 A, la tension aux bornes du moteur est inférieure à 20 V. Il faudrait augmenter la section des fils d'alimentation ( Rfil diminuerait), afin que <uM> ne devienne pas inférieure à 20 V.

retour -menu