|
Electrozingage d'une pièce en acier ( bac S Reunion 2009) |
|||||||
|
|||||||
|
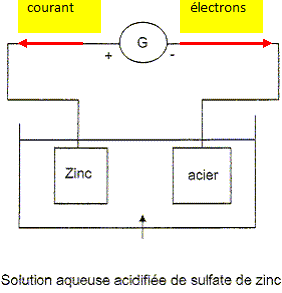
Etude du montage de l'électrolyse. Le schéma du montage est donné.. La pièce en acier est plongée dans une solution aqueuse de sulfate de zinc acidifiée ( Zn2+aq + SO42-aq). Elle est reliée au pôle négatif du générateur. La pièce en zinc est reliée à la borne positive du générateur. Indiquer le sens du courant ainsi que le sens de circulation des électrons.
On observe que la pièce de zinc se désagrège. Préciser la réaction ayant lieu au niveau de la pièce de zinc. Utiliser l'un des couples ci-dessous : Zn2+aq / Zn(s) ; O2(g) / H2O(l) ; H+aq / H2(g) A quelle électrode de zinc ou d'acier, l'oxydation a t-elle lieu ? La concentration en ion
Zn2+aq dans la solution varie
t-elle au cours de l'électrolyse ?
Justifier. Réduction des ions
Zn2+aq en zinc à la
cathode en acier négative.
Zn2+aq + 2e- =
Zn(s) Bilan : Zn(s) anode =
Zn(s) cathode. La concentration des ions
zinc Zn2+aq ne varie pas en
solution : pendant la même durée, il
en apparaît autant à l'anode qu'il
n'en disparaît à la
cathode. En milieu basique, les ions Zn2+aq peuvent réagir avec l'ion hydroxyde HO-, selon l'équation ci-dessous pour laquelle on associe la constante d'équilibre K à 25 °C. Zn2+aq + 2HO-aq = Zn(OH)2 (s). Donner l'expression de la constante d'équilibre K. K = 1 / ( [Zn2+aq] [HO-aq]2). On constate que le précipité se forme si la concentration en ion hydroxyde est supérieure à 3,16 10-9 mol/L à 25 °C. Montrer que la valeur du pH correspondant à cette concentration est égale à 5,5. Produit ionique de l'eau : Ke = [H3O+aq][HO-aq] ; [H3O+aq] = Ke / [HO-aq] = 1,0 10-14 / 3,16 10-9 = 3,16 10-6 mol/L pH = - log [H3O+aq] = = -log 3,16 10-6 =5,5. Le pH de la solution doit être inférieur à 5,5 pour réaliser cette électrolyse. Justifier. A pH >5,5 les ions zinc se trouvent sous forme d'un précipité Zn(OH)2 (s) : les ions zinc n'étant pas disponible en solution, le dépôt de zinc sur l'acier ne peut pas se réaliser.
Au cours de l'électrolyse, l'intensité I du courant est maintenue constante. La durée de passage du courant est notée Dt. On étudie la réaction qui a lieu à la cathode négative : Zn2+aq + 2e- = Zn(s) On donne : I = 2,00 A ; Dt = 40,0 min ; M(Zn) = 65,37 g/mol 1 F = 96500 C mol-1 ; NA = 6,02 1023 mol-1 ; e = 1,6 10-19 C. Quelle relation existe t-il entre la quantité de matière de zinc formé, notée nZn et la quantité de matière d'électron échangé ne- ? Zn2+aq + 2e- = Zn(s) D'après les nombres stoechiométriques de la demi-équation ci-dessus : nZn = ½ne- Montrer que la masse de zinc formé mZn peut se mettre sous la forme : mZn = IDt M(Zn) / (2F) Masse de zinc (g) = quantité de matière de zinc (mol ) fois masse molaire du zinc ( g/mol) mZn = nZn MZn = ½ne- MZn. Quantité d'électricité Q = I Dt = ne- F soit : ne- = I Dt / F. Par suite : mZn = IDt M(Zn) / (2F)
|
|||||||
|
|