Voyage d'une note bac S Nouvelle Calédonie 2008.

On appelle grandes ondes ( GO) ou ondes longues ( OL) la bande de radiofréquences qui s'étend de 30 kHz à 300 kHz. Elles sont utilisées par les stations de radio en modulation d'amplitude, pour les communications à grande distance. Cependant, depuis quelques années, leur utilisation tend à disparaître, au profit de la bande FM. Les récepteurs ne propoent désormais que rarement cette gamme. Il est encore utile de conserver un émetteur grandes ondes qui soit opérationnel aujourd'hui. La station officielle pour obtenir des informations nationales est "France Inter" de fréquence 162 kHz. D'après un site Internet. Données complémentaires : célérité des ondes électromagnétiques dans l'air : c = 3,00 108 m/s. célérité du son dans l'air vson = 340 m/s à la température de 20 °C. Intervalle de fréquences des signaux sonores audibles : 20 Hz - 20 kHz. note do3 ré3 mi3 fa3 sol3 la3 si3 do4 f(Hz) 262 294 330 349 392 440 494 523 On s'interesse dans cet exercice à la qualité de la transmission et de la réception d'une note émise par un violon lors d'un concert retransmis sur France Inter. Station émettrice. Parmi les termes proposés, choisir ceux qui conviennent pour compléter les phrases suivantes. L'onde porteuse utilisée en radio est une onde ..... sonore, lumineuse, mécanique, électromagnétique. L'onde porteuse utilisée en radio est une onde électromagnétique. cours : [ Les ondes hertziennes, utilisées pour les transmissions d'informations, sont de même nature que la lumière visible (ou autres : infra-rouge, ultra-violet, rayons gamma).] En modulation d'amplitude, l'amplitude du signal modulé est une fonction..... de la tension modulante. linéaire, exponentielle, constante, affine, sinusoïdale. En modulation d'amplitude, l'amplitude du signal modulé est une fonction affine de la tension modulante. cours : [ La tension basse fréquence module l'amplitude de la porteuse ( haute fréquence). Si la tension modulante est sinusoïdale: tension modulante basse fréquence : s(t) = Sm cos(2pfSt) + U0. tension haute fréquence (porteuse) : p(t) = Pm cos(2pfPt) la tension de sortie du multiplieur proportionnelle au produit s(t) * p(t). L'amplitude de la tension modulée est de la forme : Um(t) = A[m cos(2pfSt)+1] où m = Sm/U0, taux de modulation.] On note l la longueur d'onde de la station émettrice. Calculer la valeur de l. l = c fréquence = 3,00 108 162 103 = 1,85 103 m Analyse d'une note. 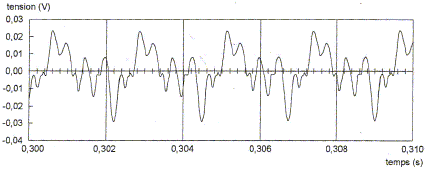Lors d'un concert, un microphone de bonne qualité, placé près d'un violon, est relié à un oscilloscope à mémoire. On capte une note. L'ozcillogramme est reproduit ci-dessous. En déterminant la fréquence fondamentale f1, montrer que celle-ci est la3 : T~ 2,25 10-3 s. 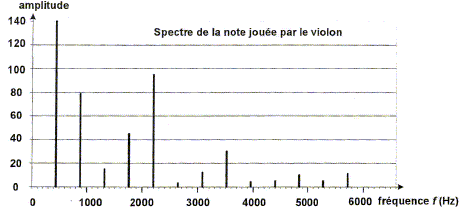f1 = 1 T 1 2,25 10-3 = 4,4 102 Hz Le spectre en fréquence de la note captée est reproduit ci-dessous : Calculer les valeurs des fréquences des harmoniques de rang 2 et de rang 13 de cette note. Les fréquences des harmoniques sont des multiples de la fréquence du fondamental. f2 = 2 f1 =4,4 102*2 = 8,8 102 Hz. f13 = 13 f1 =4,4 102*13 = 5,7 103 Hz. Transmission de la note. Dans le cas d'un signal modulant sinusoïdal, de fréquence f, d'amplitude Um et d'expression u(t) = Um cos (2 p ft), le signal modulé en amplitude peut se mettre sous la forme : s1(t) = A cos (2 p F t) +½ AUm / U0 cos (2 p (F-f) t) +½ AUm / U0 cos (2 p (F+f) t) en volts  où A et U0 sont des constantes qui dépendent de l'émetteur radio et F est la fréquence de la porteuse. France -Inter étant la station émettrice, calculer les trois fréquences intervenant dans l'expression du signal modulé s1(t) si le son transmis est celui d'un diapason qui émet un son pur correspondant à la note la3. F = 162 kHz ; f = 440 Hz ; F-f = 161,6 kHz ; F+f = 162,4 kHz. Chaque station émettrice dispose d'une bande de fréquence ( appelée canal) de 9 kHz de largeur, centrée sur la fréquence F de la porteuse. C'est pourquoi la fréquence la plus aiguë qui peut être transmise en Grandes Ondes vaut 4,5 kHz. Quelle(s) fréquence(s) du spectre de la note jouée par le violon ne peuvent pas être transmises par France Inter ?  Fréquences des harmoniques supérieures à 4500 Hz. f11 = 11 f1 =4,4 102*11 = 4,8 103 Hz ; f12 = 12 f1 =4,4 102*12 = 5,3 103 Hz ; f13 = 13 f1 =4,4 102*13 = 5,7 103 Hz ; Réception du signal. L'émission qui retransmet le concert est captée par un récepteur radio formé de plusieurs éléments connectés les uns à la suite des autres : circuit d'accord, démodulateur, amplificateur et haut parleur. Le premier module est le circuit d'accord dont le schéma est reproduit ci-dessous : s2(t) est le signal de sortie de ce premier module. Nommer les composant 1, 2, 3 et calculer la valeur de l'inductance L qui permet de capter France Inter si C = 0,47 nF. 1 : antenne ; 2 : bobine inductive d'inductance variable ; 3 : condensateur. La fréquence propre du dipôle LC est : F = 1 2p (LC)½ d'où L = 1 4 p 2F2C F= 1,62 105 Hz ; C = 4,7 10-10 F. L = 1 4 *3,14 2(1,62 105)2 4,7 10-10 =2,1 10-3 H. La qualité de la réception dépend de la valeur de la résistance R du composant 2. ( Le récepteur est d'autant plus sélectif que la valeur de R est faible ). La courbe de résonance représentée sur la figure ci-dessous représente la variation de l'amplitude S du signal s2(t) en fonction de la fréquence du signal reçu, une fois le récepteur accordé sur France Inter. 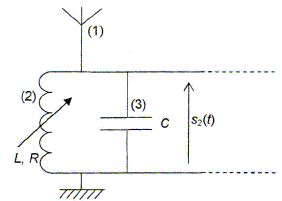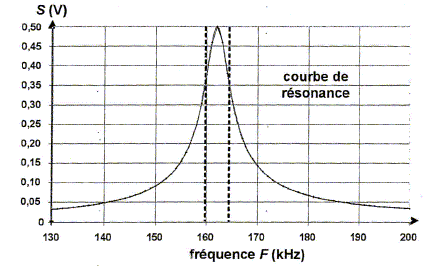Pour qu'un signal soit transmis dans de bonnes conditions par le circuit d'accord à l'élément suivant ( démodulateur), son amplitude S doit être suffisante : cette condition se traduit par S<=0,35 V. Ainsi l'intervalle des fréquences transmises au démodulateur est [160 kHz ; 164 kHz]. En supposant que les modules démodulateur, amplificateur et haut parleur sont parfaits, préciser les fréquences présentes dans le spectre de la note restituée par le haut parleur. Justifier. La valeur maximale de F + f est 164 kHz soit fmaxi = 2000 Hz. Seules les harmoniques de fréquences inférieures ou égales à 2000 Hz sont transmises. ( f2 = 880 Hz ; f3 = 1,3 kHz ; f4 = 1,76 kHz ) Comparer la hauteur et le timbre de la note restituée par le haut-parleur à la note originale émise par le violon. Justifier. Les deux notes ont la même fréquence du fondamental f1 = 440 Hz : elles ont la même hauteur. Par contre, elles ne possèdent pas les mêmes harmoniques : les timbres sont donc différents.

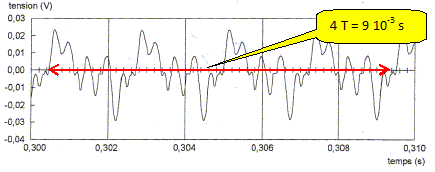retour -menu