|
Un jour d'orage : dipôle RC, onde bac S Nouvelle Calédonie 2008. |
|||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||
|
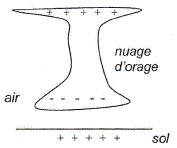
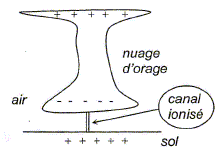
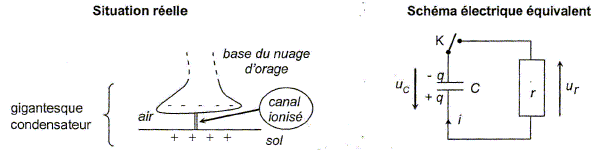
Modélisation de l'éclair nuage-sol.
Le condensateur est initialement chargé sous une tension continue U positive. A la date t=0, on ferme l'interrupteur K et la décharge débute. Montrer que l'équation différentielle vérifiée par la tension uC(t) aux bornes du condensateur pendant la décharge s'écrit :
Additivité des tensions : uC + uR =0 ; uC +r CduC/dt =0. On pose t = rC, constante de temps du circuit. Vérifier par une analyse dimensionnelle que t est homogène à un temps. r : tension / intensité ; C : charge / tension ; charge : intensité * temps.
Vérifier que l'expression uC(t) = U exp(-t/t) est solution de l'équation différentielle. Dériver uC(t) par rapport au temps : duC/dt = U/ (-t) exp(-t/t) = U/ (-rC) exp(-t/t) Repport dans l'équation différentielle : U exp(-t/t) -rC U/ (-rC) exp(-t/t) =0 Cette égalité est bien vérifiée quel que soit le temps : la fonction proposée est donc solution de l'équation différentielle.
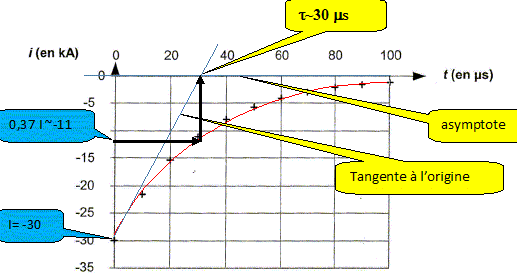
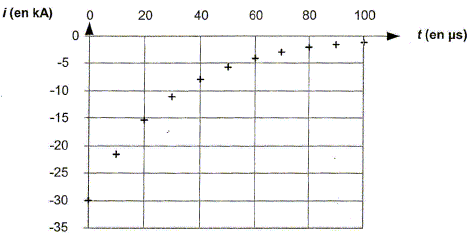
Foudre et sécurité. Lors d'une décharge atmosphérique, la foudre peut s'abattre en un point de la terre. L'intensité du courant ainsi généré peut être modélisé par une fonction du temps dont l'expression peut s'écrire : i(t) = -I exp(-t / t) avec I une constante positive. Retrouver l'expression de la fonction i(t) à partir de celle de uC(t). On exprimera I en fonction de U et r. i (t)= dq/dt et q= CuC d'où i(t) = CduC/dt. Dériver uC(t) par rapport au temps : duC/dt = U/ (-t) exp(-t/t) = U/ (-rC) exp(-t/t) Multiplier par C : i(t) = -U/ r exp(-t/t) ; I= U/r. Choisir parmi les courbes suivantes celle qui correspond à i(t). Justifier.
Courbe A : i(t) = -I exp(-t / t) L'intensité à t=0 est négative ( -30 kA) ; la fonction -I exp(-t/t) est croissante. La courbe B ne convient pas : la valeur initiale de l'intensité est positive ; la fonction proposée est décroissante.
La contraction puis la dilatation des masses d'air surchauffé sur le trajet de l'éclair ( le long du canal ionisé) créent une onde de choc qui engendre le bruit appelé "tonnerre". Donner la définition d'une onde mécanique progressive. Propagation d'une perturbation dans un milieu matériel avec transport d'énergie, sans transport de matière. Le tonnerre est-il une onde longitudinale ou une onde transversale ? Justifier. L'onde sonore est onde longitudinale : Propagation d'une variation de pression ayant la même direction que la direction de propagation de l'onde. On rappelle que le domaine des fréquences audibles par l'homme s'étend de 20 Hz à 20 kHz et que la célérité du son dans l'air vaut vson = 340 m/s à la température de 20°C. Quelles sont les longueurs d'onde l correspondant à ses fréquences ?
L'orage est tout près... Dans un livre onpeut lire : pendant un coup de foudre, l'éclair et le bruit du tonnerre se produisent en même temps. Mais comme la lumière va plus vite que le son, on voit l'éclair avant d'entendre le tonnerre. Pour savoir à quelle distance se trouve l'orage, compte les secondes entre l'éclair et le tonnerre, puis divise par trois. S'il y a six secondes, c'est que l'orage est à deux kilomètres de toi. On considère que la célérité de la lumière dans l'air est c = 3 108 m/s. Montrer que la durée
Dt
qui s'écoule entre l'éclair et le tonnerre en
fonction de la distance
d
qui sépare l'observateur de l'orage, de la
célérité du son dans l'air
vson
et de la célérité
c
de la lumière
dans l'air s'écrit
: ) Le son parcourt la même distance d pendant la durée t' = d/vson. Dt = t'-t = d/vson - d/c. Justifier le calcul proposé ci-dessus permettant de connaître la distance qui sépare l'observateur de l'orage en kilomètres ( la valeur 3 est arrondie pour simplifier le calcul destiné à un enfant). c étant très supérieur à vson, le terme 1/c est négligeable devant le terme 1/vson. d ~ Dt .vson avec vson ~ 1000 / 3 m/s ~ 1/3 km /s. d ~ Dt /3 avec d en km et Dt en seconde.
|
|||||||||||||||||||||||||||||||||||
|
|
 courbe
A
courbe
A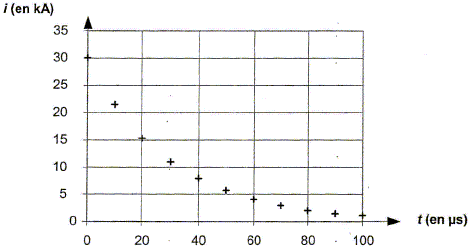 courbe
B
courbe
B