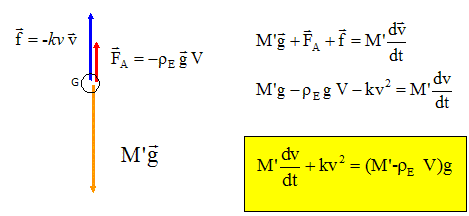A propos de sous-marins : chute dans un fluide ; fission de l'uranium 235 bac S Nouvelle Calédonie 2008.

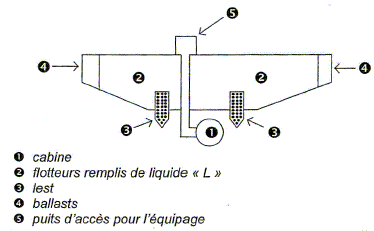
Les bathyscaphes sont des sous-marins d'exploration abyssale. En service de 1948 à 1982, ils ont été les seuls submersibles capables d'atteindre les profondeurs les plus grandes ( 10916 m dans la fosse des Mariannes, le 23 janvier 1960). Un bathyscaphe est constitué d'une lourde cabine sphérique en acier pouvant accueillir deux ou trois passagers, suspendue à un flotteur rempli d'un liquide noté L moins dense que l'eau qui compense le poids. Le bathyscaphe descend par gravitation et remonte en lâchant du lest. A cause de leur poids, les bathyscaphes ne peuvent être embarqués et sont remorqués par leur navire. Pour plonger le bathyscape remplit ses ballasts d'eau ou largue une partie du liquide L qu'il remplace par de l'eau de mer. Il s'alourdit et descend verticalement s'il n'y a pas de courant marin. Il se pose sur le fond. Pour remonter, il largue une partie de son lest. D'après un site internet. Etude de la plongée. Les mouvements sont étudiés dans le référentiel terrestre supposé galiléen. On néglige les courants marins : la descente est verticale. Masse totale du bathyscaphe M = 200 tonnes ( liquide L compris) Volume total du bathyscaphe V = 194 m3 ; intensité de la pesanteur g = 9,8 m s-2. Mase volumique : eau de mer rE=1,03 103 kg m-3 ; liquide L rL=0,66 103 kg m-3 ; Le bathyscaphe est complètement immergé mais ne plonge pas encore. Donnér l'expression littérale de la valeur FA de la poussée d'Archimède exercée sur le bathyscaphe complétement immergé. Calculer sa valeur. Valeur de la poussée : poids du volume de fluide ( eau) déplacé . FA = rEVg. FA = 1,03 103 *194*9,8 = 1,96 106 ~ 2,0 106 N. Comparer les valeurs du poids du bathyscaphe et de la poussée d'Archimède qu'il subit. Conclure. M = 200 t = 2 105 kg ; poids P = Mg = 2 105 *9,8 = 1,96 106 ~ 2,0 106 N. Le poids et la poussée d'Archimède sont deux forces opposées : elles se neutralisent ; la vitesse initiale du bathyscaphe est nulle. Le principe d'inertie indique que le bathyscaphe est immobile. On admettra que, rapidement, le bathyscaphe remplace un volume V'L du liquide L par le même volume d'eau de mer. V'L = 2,0 m3. La valeur FA de la poussée d'Archimède varie t-elle ? Justifier. Le volume du bathyscaphe reste inchangé ; le fluide d'immersion ( eau de mer) ne change pas. Si g demeure constant, alors la valeur de la poussée d'Archimède reste constante. Déterminer l'expression littérale de la variation de masse du bathyscaphe ( notée DM positive). Faire le calcul. La masse diminue de : V'L rL ; la masse augmente de : V'L rE . DM = V'L rE - V'L rL = V'L(rE -rL) =2,0 (1,03-0,66) 103 = 7,4 102 kg. Expliquer pourquoi le bathyscaphe se met à descendre. La poussée d'Archimède reste constante tandis que le poids augmente : la somme vectorielle des forces appliquées au bathyscaphe n'est plus nulle. La valeur du poids étant devenue supérieure à celle de la poussée, le bathyscaphe descend. Plongée du bathyscaphe. On considère que la messe totale du bathyscaphe est M' = 200,74 t. Faire un bilan des forces exercées sur le bathyscaphe qui descend. Représenter sans échelle ses forces sur un schéma. Etablir l'équation différentielle du mouvement selon un axe vertical descendant. On suppose que l'expression de la force de frottement fluide exercée par l'eau de mer est modélisée par la relation f = k v2 où k est une constante positive qui dépend de la forme de l'objet et de la nature du fluide. Poids vertical, vers le bas, valeur M'g Poussée d'Archimède, verticale vers le haut, valeur FA = rEVg force de frottement fluide f, verticale vers le haut, valeur f = k v2 La vitesse limite atteinte par le bathyscaphe est vlim = 1,0 m/s. Déterminer l'expression littérale de cette vitesse limite. En déduire la valeur de k en justifiant l'unité par analyse dimensionnelle. La vitesse limite est constante ; sa dérivée par rapport au temps est nulle. L'équation différentielle précédente s'écrit : kv2lim = (M'-rEV)g vlim= [ (M'-rEV)g k ]½ d'où k = (M'-rEV)g v2lim = (2,0074 105-194*1,03 103)*9,8 1,0 =9,0 103 kg m-1 k v2 a la dimension d'une force soit une masse * une accélération ( accélération = longueur / temps2 ) [k v2] = M L T-2 ; Une vitesse est une longueur divisée par un temps : [v] = L T-1 ; [v2] = L2 T-2 ; [k]= M L T-2 L-2 T2 = M L-1. La propulsion du sous-marin "le terrible". D'abord propulsé par des moteurs Diesel rechargeant des batteries, les sous-marins ne pouvaient pas rester en plongée très longtemps car pour utiliser leur moteur, ils devaient obligatoirement faire surface pour évacuer les gaz d'échappement des moteurs. Tout changea avec la propulsion nucléaire : ce n'était plus la propulsion qui limitait la plongée mais la résistance physique de l'équipage. Dans cette partie, on se propose d'étudier le mode de propulsion du dernier sous-marin nucléaire français " le Terrible" qui entrera bientôt en service. Un tel sous marin utilise comme combustible de l'uranium enrichi en isotope 23592U ( cet isotope est fissile). Données : noyau 23592U 9438Sr 14054Xe 10n masse (u) 235,0439 93,9154 139,9252 1,0087 1 u = 1,66 10-27 kg ; c = 3,00 108 m/s ; NA =6,02 1023 mol-1 ; masse molaire de 23592U : 235 g/mol. Donner la structure du noyau noté 23592U. 92 protons et 235-92 = 143 neutrons. Les noyaux d'uranium 235 peuvent subir différentes fissions. La plus fréquente est donnée par l'équation suivante : 23592U +10n --> 9438Sr + 14054Xe + x 10n Montrer que x=2. Justifier. Conservation du nombre de nucléons : 235+1 = 94 + 140 +2x d'où x = 2. Montrer que l'énergie libérée par la fission, selon l'équation ci-dessus, d'un noyau d'uranium 235 vaut Elib = 2,91 10-11 J. Variation de masse Dm = m(10n) + m(14054Xe) + m( 9438Sr) - m(23592U) Dm = 1,0087 +139,9252 +93,9154-235,0439=-0,1946 u -0,1946*1,66 10-27 = -3,230 10-28 kg. Cette diminution de masse s'acompagne de la libération d'énergie dans le milieu extérieur ( ce que traduit le signe négatif) : Dm c2 = -3,230 10-28 *(3,00 108)2 = -2,91 10-11 J Energie libérée : 2,91 10-11 J. On suppose pour simplifier, que les énergies libérées par toutes les réactions de fission sont approximativement égales à celle calculée ci-dessus. Le réacteur fournit une puissance moyenne P= 150 MW. On rappelle que 1 W = 1 J/s. Montrer qu'il se produit 5,15 1018 fissions par seconde. 150 MW = 1,50 108 W ( ou J/s) 1,50 108 / 2,91 10-11 =5,15 1018 En déduire que la masse d'uranium consommée en 1 s vaut 2,01 10-3 g. Dans une mole d'uranium il y a 6,02 1023 atomes ; nombre de fissions par seconde : 5,15 1018 Quantité de matière (mol) d'uranium ayant réagi à chaque seconde : 5,15 1018 /6,02 1023 =8,555 10-6 mol. masse (g) = n(mol) * masse molaire uranium ( g/mol) m = 8,555 10-6 *235 = 2,01 10-3 g. Un tel sous-marin est prévu pour naviguer pendant une durée de 2 mois. Quelle masse minimale d'uranium 235 devra t-il embarquer pour assurer son approvisionnement en énergie pendant cette durée ? Données : 1 mois = 2,6 106 s. 2*2,6 106 s *2,01 10-3 =1,0 104 g = 10 kg.

retour -menu