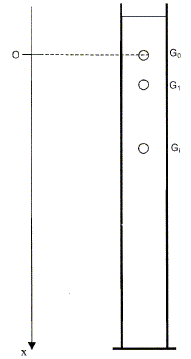
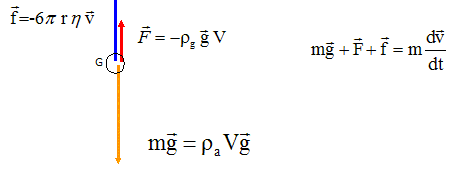Une éprouvette contenant un liquide visqueux
sert de support à l'étude de la chute d'une
bille d'acier. Le schéma ci-dessous, qui donne une
idée du montage, n'est qu'indicatif. En particulier,
il ne respecte pas d'échelle et ne peut pas servir de
support pour des mesures.
Les vecteurs sont écrits
en gras et en bleu.
|
La bille, qui constitue le système
étudié, est lâchée sans
vitesse initiale à l'instant t 0. Au
même instant, une acquisition vidéo
assurée par une webcam couplée
à un ordinateur est déclenchée
de manière à enregistrer 25 images
par seconde. La position instantanée x du
centre G de la bille est repérée par
l'axe vertical orienté vers le bas Ox, de
vecteur unitaire
i .
A t =0, G est en G0.
Le vecteur-vitesse de G est noté
v =
v. i
.
La vidéo est ensuite analysée
à l'aide d'un logiciel approprié qui
permet de repérer aux dates t i
les positions successives x i de G lors
de son mouvement descendant et de calculer
approximativement la vitesse moyenne v i
entre les dates t i -1 et t i +
1.
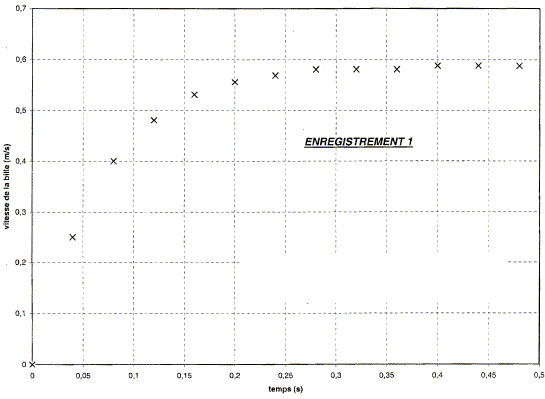
La détermination des vitesses v
i aux instants t i donne
l'enregistrement suivant :
|
Expliquer comment le
logiciel permet de déterminer les vitesses
v
i à partir
des positions x
i aux
instants t
i.
Calcul de la vitesse moyenne sur
une durée aussi petite que possible ( deux fois la
durée séparant deux images
consécutives)
v i = (
x i +1 - x i - 1 ) / ( t i
+1 - t i - 1)
Mettre en évidence
l'existence d'une vitesse limite
VL
dont on donnera la
valeur.
Equation du mouvement.
On considère comme système la bille
plongée dans le liquide et en mouvement par rapport
à celui-ci.
Faire le bilan des forces qui
s'exercent sur le système. Les représenter sur
un schéma.
La bille est soumise à son poids, à la
poussée d'Archimède et à une force de
frottement fluide.
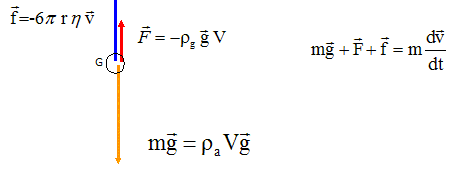
On note m et V la masse et le volume de la
bille,
ra et
rg
les masses volumiques respectives de l'acier qui constitue
la bille et du liquide dans laquelle celle-ci est
plongée.
g=
g
i est
l'accélération de la pesanteur.
On suppose que la force (" résistance" )
exercée par le fluide sur la bille en mouvement est
de la forme
F=
-k v, k
étant une constante positive.
Déterminer
l'équation différentielle
vérifiée par la fonction v(t). Montrer qu'elle
est de la forme : dv/dt = -k/m v +
ag.
Ecrire la seconde loi de Newton suivant l'axe vertical
descendant :
mg - rg
V g - k v = m dv/dt avec m = ra
V soit V = m / ra
mg - m rg/
ra
g - k v = m dv/dt
mg( 1-rg
/ ra)
- k v = m dv/dt
dv/dt = -k/m v +g( 1-rg
/ ra)
; on pose a = (
1-rg
/ ra)
Vérifier que la
fonction v(t) =
a
g m/k [ 1-exp(-k/m t)]
est solution de
l'équation précédente et vérifie
la condition initiale à t =0, v
=0.
dv/dt = a
g exp(-k/m t), repport dans l'équation
différentielle :
a
g exp(-k/m t) =- a
g [ 1-exp(-k/m t)] + ag.
a
g exp(-k/m t) =- a
g +a
g exp(-k/m t)+ ag.
Cette égalité est
vérifiée quelque soit le temps. La fonction
proposée est bien solution de l'équation
différentielle.
v(t) = a
g m/k [ 1-exp(0)] = a
g m/k [ 1-1] = 0.
|
|
On prend
dorénavant les valeurs suivantes,
données dans le système international
SI :
m =5,00.10-3 kg
; g = 9,81 m.s-2·; k =
7,60.10-2 kg.s-1 ;
a=
0,906.
Dans l'équation
différentielle ou dans l'expression de la
solution, mettre en évidence l'existence
d'une vitesse limite. Calculer sa valeur et la
comparer à celle trouvée
ci-dessus.
exp(-k/m t) tend vers
zéro au bout d'un temps très grand :
la vitesse tend vers VL=
a
g m/k .
VL=
0,906*9,81*5,00.10-3 /
7,60.10-2
=0,585
m/s, valeur en
accord avec celle trouvée
graphiquement.
Utiliser l'analyse
dimensionnelle pour déterminer
l'unité de
m/k
.
m : masse ; [m]=
M
k est une force
divisée par une vitesse ; une force est une
masse fois une accélération ; une
accélération est une longueur
divisée par un temps au carré. [k
] = M T-1.
[m/k] =
T.
Calculer
numériquement ce
rapport.
m/k = 5,00.10-3
/ 7,60.10-2
=6,58
10-2
s.
Quelle
interprétation peut-on donner de cette
grandeur
?
m/k est la constante de
temps du système : au bout d'une
durée voisine de 5 m/k, la vitesse limite
est pratiquement atteinte.
|
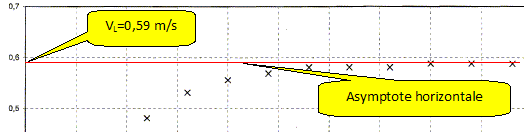
Par une méthode de votre
choix et que vous expliciterez, déterminez sur
l'enregistrement la valeur du temps t
caractéristique du phénomène.
Conclusion.
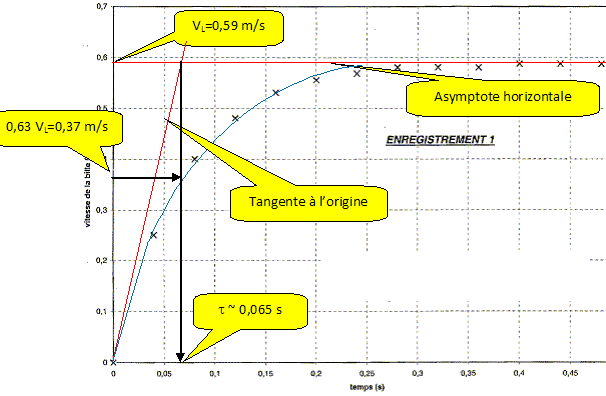
On retrouve la valeur
calculée ci-dessus.