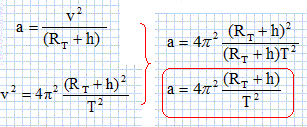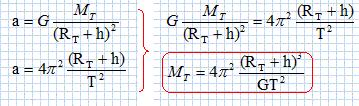Détermination de la capacité d'un condensateur ( bac S Asie 2009)

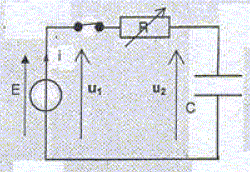
On se propose de déterminer la capacité d'un condensateur à partir de deux méthodes différentes. On dispose du matériel suivant : - un générateur de tension continue e = 20 V - une boîte de résistance étalonnées R(x1 W, x10 W, x100 W, x1000 W ) - une bobine idéale d'inductance L 0,50 H et de résistance nulle - un condensateur de capacité C inconnue - un ordinateur relié au montage par une interface et permettant d'enregistrer des variations de tensions et d'intensité au cours du temps - un interrupteur et des fils de connexion sécurisés. Méthode 1. A l'aide d'un ordinateur on enregistre les variations au cours du temps des deux tensions u1 et u2 à partir de l'instant de la fermeture de l'interrupteur, choisi comme origine des dates. On donne les graphes obtenus pour différentes valeurs de la résistance R.   Compléter le tableau en indiquant danns chaque case, le numéro de la courbe qui convient. R(ohms) 400 800 1200 1600 courbe représentant u1 1 1 1 1 courbe représentant u2 2 3 4 5 La durée de la charge est environ égale à 5 RC : la durée de la charge est d'autant plus grande que R est grand ( à capacité constante).  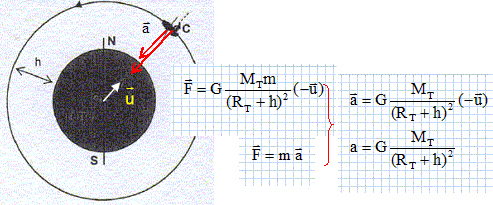Compléter le tableau ci-dessous après avoir déterminé la constante de temps t correspondant à R = 1600 ohms en expliquant la méthode utilisée. Dans un référentiel galiléen, la somme vectorielle des forces appliquées au satellite de masse m, est égale au produit de la masse m du satellite par le vecteur accélération de son centre de d'inertie. En déduire une représentation du vecteur accélération ( sans soucis d'échelle). En déduire que la valeur de l'accélération a du centre d'inertie du satellite est : a=GMT/ (RT+h)2. Le satellite est soumise à la seule force de gravitation exercée par la Terre ; de plus la masse est positive : le vecteur accélération est colinéaire et de même sens que la force de gravitation. Quelles propriétés a le vecteur accélération si le mouvement est circulaire uniforme ? Montrer que ses propriétés sont vérifiées ici. Le vecteur accélération est centripète ; sa valeur est constante égale à v2/(RT+h). - Le satellite est soumise à la seule force de gravitation exercée par la Terre ; de plus la masse est positive : le vecteur accélération est colinéaire et de même sens que la force de gravitation. - Dans l'expression de l'accélération, toutes les grandeurs sont des constantes. Donner l'expression de la vitesse v, supposée constante, du centre d'inertie C du satellite en fonction de RT, h et T. Le satellite décrit une circonférence de rayon RT+h, à la vitesse v durant une période T. 2 pi (RT+h) = v T ; v = 2 pi (RT+h) / T. Donner l'expression de l'accélération a du centre d'inertie du satellite en fonction de v, RT, h. En déduire l'expression de l'accélération en fonction de RT, h et T. En identifiant les expressions de l'accélération, exprimer la masse MT de la terre en fonction des données de l'énoncé et calculer sa valeur. ( Le résultat sera donné avec un seul chffre significatif pour cette question). (RT+h)3 = (6,38 106 + 8,30 105)3 = (7,21 106)3~ 4 1020 T2 = (101*60)2 = (6,06 103)2~ 4 107 ; 4 pi2 / (6,67 10-11) ~6 1011 ; MT ~6 1011*4 1020 / 4 107 ~ 6 1024 kg. Le satellite est-il géostationnaire ? Justifier. Le satellite n'est pas géostationnaire : - d'une part son orbite n'est pas dans le plan équatorial - d'autre part, sa période de révolution n'est pas 24 heures. 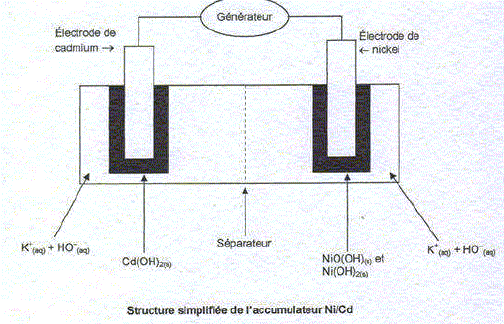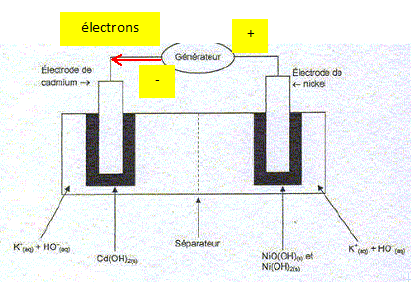Partie 2 : Compte tenu de l'orbite choisie pour le satellite SPOT 4, son générateur solaire se trouve dans l'ombre de la Terre à chaque révolution pendant une durée d'environ 35 min et éclairé durant 65 min. Le courant n'est généré par les cellules que pendant les périodes éclairées. Il faut donc un élément capable de stocker l'énergie pendant le "jour" et de la restituer pendant la "nuit" pour alimenter de façon permanente le satellite. De même pendant le lancement, avant que le générateur solaire ne soit déployé,l'alimentation du satellite doit être assurée. Pour cela 4 batteries de 40 hA, pesant près de 45 kg chacune, sont embarquées sur SPOT 4 pour répondre à la consommation d'énergie électrique du satellite. Elles sont composées chacune de 24 accumulateurs nockel-cadmium. A chaque révolution, les batteries effectuent un cycle complet décharge-recharge. Pour tenir les 5 années de vie souhaitée, ce qui représente 25 000 cycles, une gestion très fine des batteries s'impose. L'accumulateur nickel-cadmium est composé d'une électrode de nickel et d'une électrode de cadmium, plongées dans un électrolyte et séparées par une paroi poreuse. les deux couples oxydant-réducteur mis en jeu sont : NiO(OH) (s) / Ni(OH)2 (s) et Cd(OH)2 (s) / Cd(s). Par souci de simplification, on étudiera uniquement l'accumulateur nickel-cadmium lors de sa charge et on considèrera qu'il est relié à un générateur. On donne les deux demi-équations électroniques associées à cet accumulateur : NiO(OH) (s) + H2O (l) + e- = Ni(OH)2 (s) + HO-(aq) et Cd(OH)2 (s) + 2e- = Cd(s)+ 2HO-(aq) Sachant que du cadmium solide se forme, écrire l'équation globale lors de la charge de cet accumlateur. Cd(OH)2 (s) + 2e- = Cd(s)+ 2HO-(aq) et 2Ni(OH)2 (s) + 2HO-(aq) = 2NiO(OH) (s) + 2H2O (l) + 2e- ; Ajouter : Cd(OH)2 (s) + 2e- +2Ni(OH)2 (s) + 2HO-(aq)= Cd(s)+ 2HO-(aq)+2NiO(OH) (s) + 2H2O (l) + 2e- ; Simplifier : Cd(OH)2 (s) +2Ni(OH)2 (s) = Cd(s)+2NiO(OH) (s) + 2H2O (l). Indiquer sur le schéma le sens de déplacement des électrons pendant la charge et la polarité des bornes du générateur relié à l'accumulateur. A quelle électrode s'effectue la réduction lors de la charge ? La réduction de Cd(OH)2 (s) en Cd(s) nécessite l'apport d'électrons ; une réduction s'effectue à la cathode négative, l'électrode de cadmium. La masse de métal nickel va t-elle augmenter, diminuer ou rester constante durant la charge ? Justifier. Oxydation à l'anode positive : 2Ni(OH)2 (s) + 2HO-(aq) = 2NiO(OH) (s) + 2H2O (l) + 2e- Le nickel métal n'intervient pas : la masse de nickel reste donc constante. Sachant que l'électrolyte est formé d'ions K+(aq) et HO-(aq), indiquer les sens de déplacement de ces ions lors de la charge de l'accumulateur. 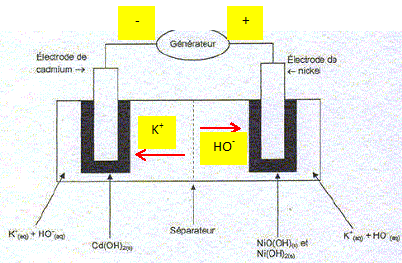Exprimer la charge électrique Q de 40 Ah indiquée dans le texte, dans l'unité du système internationnal. 40 *3600 = 1,44 105 C~1,4 105 C. Calculer la durée minimale théorique de charge d'une batterie complètement déchargée lorsque l'intensité du courant de charge est constante I = 10 A. t = Q/I = 1,44 105/10 = 1,44 104 s~1,4 104 s. ou 40 /10 = 4,0 heures.

retour -menu