|
|
Martin
est passionné par l'observation du ciel. Il demande à son professeur de
sciences physiques de lui donner quelques explications à propos des
lunettes astronomiques. Celui-cl propose de modèliser une lunette en
utilisant deux lentilles convergentes. Il lui rappelle également que
toute lentille possède un centre optique 0, un foyer image F', un foyer
objet F.
Étude
d'une lentille convergente.
Soit la lentille L, de distance focale f' =2,0 cm.
Par
quelle relation définit-on la distance focale d'une lentille ?
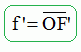
Calculer
la vergence C de cette lentille.
f' = 2,0 10-2 m ; C = 1/f' = 1/2,0 10-2 = 50 dioptries.
Placer
sur l'annexe le centre optique 0, le foyer image F', le foyer objet F.
Construire,
sur l'annexe l'image A'B' par la lentille L de l'objet.
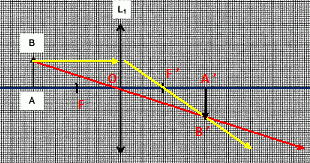
Vérification de la position et de
la taille de l'image A'B' par le calcul.
Données: OA = 4,0 cm ;
AB = 1,5 cm.
Utiliser
la formule de conjugaison pour déterminer la position de l'image A'B'.
Utiliser
la formule du grandissement pour déterminer la taille de l'image A'B'.
Modélisation de
la lunette.
On appelle objectif la lentille située du côté de l'objet à observer,
et oculaire celle située du côté de l'oeil de l'observateur.
Données : objectif : lentille L1 de distance focale f'1 =
1,00 m et de diamètre 6 cm.
oculaire: lentille L2 de
distance focale f'2 =
20,0 cm et de diamètre 6 cm.
Où
se situe l'image par l'objectif d'un objet à l'infini ? Cette
image est appelée image intermédiaire.
L'image d'un objet situé à l'infini se situe dans le plan focal
image de la lentille objectif L1.
Où
doit se situer l'image intermédiaire pour être vue à travers l'oculaire
sans accommoder ?
L'oeil observe sans accomoder un objet situé à l'infini. L'image
définitive doit se trouver à l'infini ; l'image intermédiaire
doit se trouver dans le plan focal objet de l'oculaire.
Préciser
la position du foyer objet F2 de l'oculaire par
rapport au foyer image F'1 de l'objectif.
Le foyer objet F2 de
l'oculaire et le foyer image F'1 de
l'objectif sont confondus.
On dit qu'une telle lunette est
afocale.
Placer la lentille L2 sur l'annexe (échelle 1/10ème
).
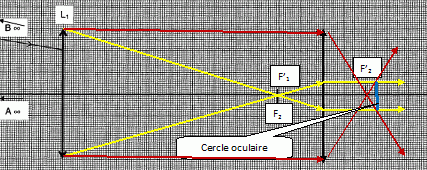
Construire,
sur l'annexe, l'image A1B1 dite image intermédiaire,
de AB par L1 puis l'image A2B2 de A1B1 par L2.
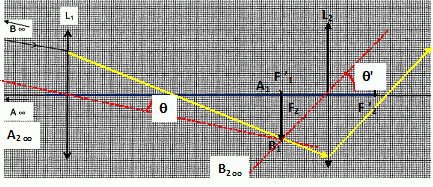
Le diamètre apparent
de l'objet AB situé à l'infini est noté q et celui de l'image
définitive A2B2 est noté q' .
Définir le diamètre apparent d'un objet.
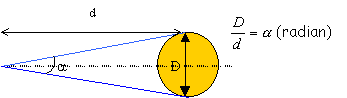
a
: diamètre
apparent
Représenter q et q' sur l'annexe à rendre avec la copie.
voir schéma ci-dessus
Le grossissement G de la lunette est défini par le rapport q' / q .
Établir la relation donnant G en fonction de f1', et f'2 puis calculer sa valeur.
tan q =A1B1 / f'1 ~q ; tan q' =A1B1 / f'2 ~q'
G = q' / q =f'1 / f'2 =1,00 / 0,200 = 5,00.
Définir le cercle oculaire et le construire sur l'annexe.
Le cercle oculaire est l'image de la monture de l'objectif donnée par l'oculaire.
|
|
Donner
l'expression vectorielle de la force de rappel notée F exercée
par le ressort.
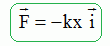
Au cours de la compression du ressort, la force exercée par
l'opérateur et notée Fop
est
à chaque instant opposée à la force de rappel du ressort F.
En déduire
l'expression vectorielle de la force Fop.
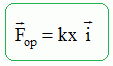
Montrer que le
travail de la force Fop
entre les points 0
et C a pour expression :
W= ½k XC2.
Le travail de Fop
a uniquement contribué à augmenter l'énergie potentielle élastique du
ressort. Si on considère que, après avoir été relâché, celui-ci la
restitue entièrement à la bille
sous forme d'énergie cinétique, exprimer XC en fonction de v0, m et k.
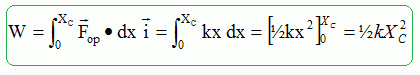
Calculer la
coordonnée Xc pour que V0 ait la valeur 2,0 m.s-1,
½k XC2 = ½mv02 ; XC2
=mv02/k
Prendre la racine négative de cette équation car le point C
est à gauche de O.
XC = -v0
(m/k)½ =
-2,0 (0,060/50)½ =0,069 m = -6,9 cm.
|
|
|