|
|
On
souhaite préparer le départ d'une bille pour un «dominos-cascade". La
bille lancée doit aller percuter le premier domino pour déclencher les
chutes en cascade. Les dominos étant déjà tous installés, on ne peut
pas faire d'essais: les conditions de lancer et la trajectoire doivent
donc être calculées.
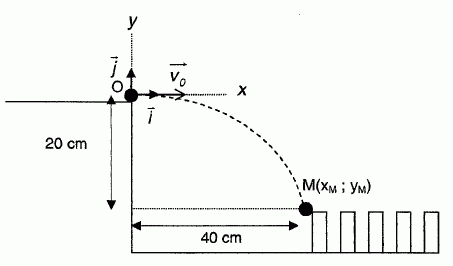
Le schéma ci-dessous (figure 1) décrit la situation. Attention, les
échelles ne sont pas respectées.
On suppose dans l'ensemble de l'exercice que :
-le référentiel terrestre est galiléen le temps de l'expérience ;
- la bille est assimilée à un point matériel ;
- les frottements solides et fluides sont négligeables.
On prendra g= 9,8 N.kg-1.
La masse de la bille est m = 60 g.
Equation
de la trajectoire.
Les
vecteurs sont écrits en gras et en bleu.
On suppose dans cette partie que la bille arrive en 0 de coordonnées (0
; 0) avec une vitesse V0
= V0 i de direction horizontale.
L'instant où la bille arrive en ce point sera pris comme origine des
temps (t = 0).
A
quelle force est soumise la bille entre les points 0 et M exclus.
La bille n'est soumise qu'à son poids, les frottements étant négligés.
En
appliquant la seconde loi de Newton à la bille lorsqu'elle a quitté le
point 0, établir la relation entre le vecteur accélération du centre
d'inertie de la bille a et le vecteur
accélération de pesanteur g.
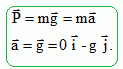
On montre que les coordonnées du vecteur vitesse du centre d'inertie de
la bille dans le repère (0,i ,j ) sont: vx(t)=v0
et vy(t)=-gt
Montrer
alors que l'équation de la trajectoire du centre d'inertie de la bille
entre 0 et M est :
|
|
y(x)
= -gx2 / (2v02).
Le vecteur position est une primitive du vecteur vitesse :
x(t) = v0t + x0 avec x0 = 0. ( origine
du repère) ; d'où : t = x / v0.
y(t)
= -½gt2 + y0 avec y0
= 0. ( origine du repère)
.
|
Calculer v0 pour que le centre d'inertie de
la bille arrive en M dont les coordonnées dans le repère sont xM
= 0,40 m et yM = - 0,20 m.
v02= -gx2 / (2y) ; v0= x (-g/(2y))½
=0,40
(-9,8 /(-0,40))½ =1,98 ~2,0 m/s.
Solutions
techniques pour que la bille arrive en 0 avec la vitesse V0 .
Utilisation
d'un plan incliné:
Dans cette situation (illustrée par la figure 2
ci après), la bille est lâchée sans vitesse initiale d'un point A ( de coordonnées XA et YA)
situé en haut d'un plan incliné réglable très lisse sur lequel la bille
glisse sans frottement.
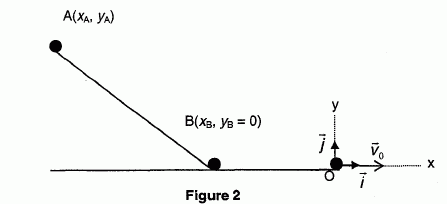
Ensuite, la bille roule entre les points B et
O : sur cette portion on considèrera que la valeur de la vitesse du
centre d'inertie de la bille reste constante; ainsi on aura VB
= V0.
Sur la portion AB, on peut considérer que la bille est soumise à deux
forces constantes: le poids P et la réaction du plan incliné R. En un
point quelconque du trajet AB, ces vecteurs forces sont représentés sur
la figure 3 ci après (représentation sans considération d'échelle).
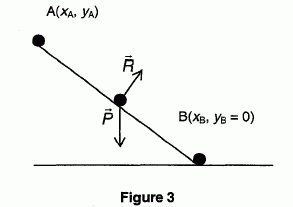
La
force R dont la direction est constamment perpendiculaire au trajet AB
n'effectue aucun travail.
Ainsi, la seule force qui effectue un travail sur le trajet AB est le
poids P qui est une force conservative: on peut donc affirmer que
l'énergie mécanique du système {bille-Terre} se conserve entre A et B.
L'origine des énergies potentielles de pesanteur est prise au point O
d'altitude YO =0. On a donc Ep(O) = 0.
Établir
l'expression de l'énergie mécanique EM(A) de la bille en A
en fonction de YA.
L'énergie mécanique est la somme de l'énergie potentielle et de
l'énergie cinétique.
La bille étant lâchée sans vitesse en A, l'énergie cinétique en ce
point est nulle.
L'énergie potentielle en A vaut Ep(A) = mgyA.
Par suite : EM(A)
=Ep(A)
= mgyA.
Établir l'expression
de l'énergie mécanique EM(B) de la bille en B
en fonction de VB.
L'énergie mécanique est la somme de l'énergie potentielle et de
l'énergie cinétique.
B est l'origine de l'énergie potentielle.
L'énergie cinétique en B vaut Ec(B) = ½mvB2.
Par suite : EM(B)
=Ec(B)
= ½mvB2.
En
déduire l'expression de YA en fonction de VO = VB.
Conservation
de l'énergie mécanique entre A et B : EM(A)
= EM(B)
mgyA=½mvB2
; yA=vB2 /(2g).
Calculer
YA pour que va ait la
valeur de 2,0 m.s-1.
yA=vB2 /(2g) =4,0/(2*9,8)
=0,204 ~ 0,20 m.
Utilisation
d'un canon à bille :
Si on ne dispose pas de la place nécessaire à l'installation du plan
incliné précédent, on peut utiliser un petit canon à ressort de raideur
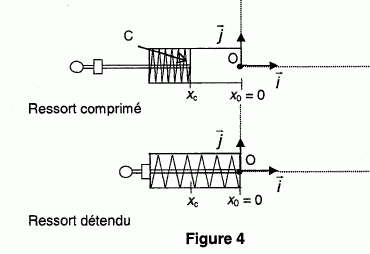
k = 50 N.m-1 (voir figure 4 ci après).
Le ressort au repos a son extrémité en O de coordonnées (0, 0).
L'opérateur le comprime en exerçant une force notée Fap jusqu'à ce que son extrémité
soit en C de coordonnées (xc, 0).
On pose alors la bille au contact du ressort. On admet que l'abscisse
de la bille (assimilée à un point matériel) est confondue avec
l'abscisse de l'extrémité du ressort est repérée par x. Lorsqu'on lâche
le tout, la bille acquiert de la vitesse. Un système de blocage limite
la détente complète en arrêtant le ressort au point O (de coordonnées 0
; 0).
|
|
Donner
l'expression vectorielle de la force de rappel notée F exercée
par le ressort.
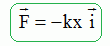
Au cours de la compression du ressort, la force exercée par
l'opérateur et notée Fop
est
à chaque instant opposée à la force de rappel du ressort F.
En déduire
l'expression vectorielle de la force Fop.
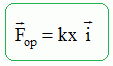
Montrer que le
travail de la force Fop
entre les points 0
et C a pour expression :
W= ½k XC2.
Le travail de Fop
a uniquement contribué à augmenter l'énergie potentielle élastique du
ressort. Si on considère que, après avoir été relâché, celui-ci la
restitue entièrement à la bille
sous forme d'énergie cinétique, exprimer XC en fonction de v0, m et k.
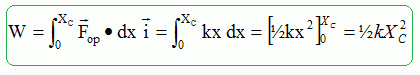
Calculer la
coordonnée Xc pour que V0 ait la valeur 2,0 m.s-1,
½k XC2 = ½mv02 ; XC2
=mv02/k
Prendre la racine négative de cette équation car le point C
est à gauche de O.
XC = -v0
(m/k)½ =
-2,0 (0,060/50)½ =0,069 m = -6,9 cm.
|
|
|