Un cycliste écologique : pile saline, condensateur ( bac S Antilles 2009)

Philippe, soucieux de l'avenir de notre planète, fait la plupart de ses déplacement à vélo. Un jour son gran père l'interpelle : " tu sais que les piles salines de ton éclairage sont polluantes et ont une durée de vie limitée ?" Philippe un peu penaud, répond " oui, mais comment faire autrement ," - et bien, il faut utiliser une dynamo, pardi ! - j'y ai bien pensé grand père mais cela ne donne de la lumière que quand on roule C'est un peu dangereux ! - oh, il doit bien y avoir une solution.. toi qui est si fort en physique, tu peux sans doute trouver une solution ! Etude de la pile saline. Fonctionnement de la pile. Dans la pile saline utilisée l'équation de la réaction se produisant à une des deux électrodes est : Zn(s) = Zn2+aq + 2e-. Cette électrode est-elle l'anode ou la cathode ? Justifier. La demi-équation ci-dessus correspond à l'oxydation du zinc ; une oxydation se produit à l'anode. Des électrons sont libérés, l'anode est la borne négative de la pile. Le couple mis en jeu à la seconde électrode est MnO2 / MnO2H. Ecrire l'équation de la réaction ayant lieu à cette électrode. L'oxydant MnO2 se réduit : MnO2 (s)+ H+ aq+e- = MnO2H (s). ou bien MnO2 (s)+ H2O(l) + e- = MnO2H(s) + HO-aq. En déduire la réaction globale de fonctionnement de la pile. Zn(s) = Zn2+aq + 2e-. 2MnO2 (s)+ 2H+ aq+2e- = 2MnO2H (s). Additionner et puis simplifier : 2MnO2 (s)+ 2H+ aq+Zn(s) = 2MnO2H (s) + Zn2+aq. ou bien : Zn(s) = Zn2+aq + 2e-. 2MnO2 (s)+ 2H2O(l) + 2e- = 2MnO2H(s) + 2HO-aq. Additionner et puis simplifier : 2MnO2 (s)+ 2H2O(l) +Zn(s) = 2MnO2H(s) + 2HO-aq+Zn2+aq. Usure de la pile. Le constructeur de la pile indique la quantité maximale d'électricité que peut débiter la pile en ampère-heure : Qmax = 1,35 Ah ( 1 Ah = 3,6 103 C ). Si l'intensité du courant débité par la pile est I = 90,0 mA, déterminer la durée maximale tmax de fonctionnement de la pile. Quantité d'électricité Qmax = I tmax ; tmax = Qmax / I =1,35*3600 / 0,090 =5,40 104 s. ( 15,0 heures ) Déterminer la quantité d'électrons n(e-) mise en jeu pendant la durée tmax. On donne 1 F = 9,65 104 C mol-1. Quantité d'électricité Qmax = F n(e-). n(e-)= Qmax / F = 1,35*3600 /9,65 104 =5,04 10-2 mol. En déduire la masse m de zinc consommée pendant cette même durée. M(Zn) = 65,4 g/mol. n(Zn)= ½n(e-) puis m = n(Zn) M(Zn) ; m = ½n(e-)M(Zn). m=5,04 10-2 * 65,4 / 2 = 1,65 g. Tentative de remplacement des piles. Une dynamo ou alternateur est un générateur de tension alternative uniquement quand le vélo roule. Un circuit électrique ( non étudié ici ) permet de transformer la tension alternative en tension continue. On peut stocker l'énergie dans un condensateur et ensuite utiliser cette énergie stockée pour faire briller la lampe. La charge du condensateur se fait pendant que le vélo roule. Quand le vélo s'arrête, un circuit électronique permet de commencer la décharge du condensateur dans la lampe. Etude expériemntale de la décharge du condensateur. 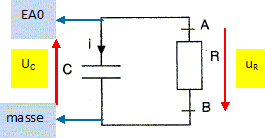Pour savoir si son idée est utilisable, Philippe décide de tester la décharge d'un condensateur de capacité C = 1,0 µF dans une lampe. On considère que la lampe à incandescence se comporte pratiquement comme un conducteur ohmique de résistance constante et de faible valeur ( 22 ohms) ; elle sera notée R dans la suite de l'exercice. Le schéma suivant représente une partie du circuit utilisé par Philippe ( celle qui correspond à la décharge du condensateur). On n'étudiera pas la charge du condensateur et on considèrera qu'à l'instant t=0 le condensateur est chargé de telle manière que la tension uC(0) = 6,0 V. Sur le schéma représenter en convention récepteur la tension uR aux bornes du conducteur ohmique ainsi que la tension uC aux bornes du condensateur. Indiquer les branchements à effectuer pour enregistrer la courbe uC = f(t) sur la voie O de l'interface notée EA0. 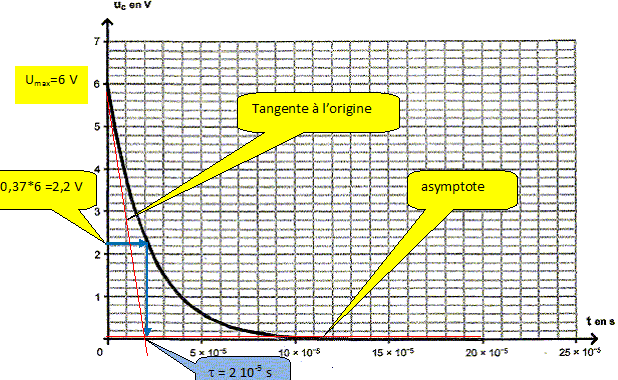Philippe utilise le logiciel pour tracer la courbe | i | = f(t). On donne les courbes obtenues. Déterminer la constante de temps t du circuit en faisant apparaître les tracés. Enoncer la relation qui permet de calculer la constante de temps t de ce circuit. t = RC. Vérifier que t est homogène à un temps par une analyse dimensionnelle. R est homogène à une tension divisée par une intensité : [R] = U I-1. C est homogène à une charge divisée par une tension ; une charge est une intensité fois un temps : par suite [C] = I T U-1. En conséquence : [RC] = T ; la constante de temps est bien homogène à une temps. Calculer la valeur théorique de la constante de temps. t = RC = 22*1,0 10-6 = 2,2 10-5 s. écart relatif avec la valeur expérimentale : (2,2-2 ) / 2 *100 = 10 %. ( l'échelle des temps sur le graphe n'est pas très précise). A 10 % près les deux valeurs sont en accord. La décharge du condensateur dans la lampe du vélo doit permettre d'avoir de la lumière à l'arrêt pendant au moins 3 min ( durée du feu au bout de la rue de Philippe). Philippe a testé sa lampe et il sait qu'elle brille correctement si la valeur absolue de l'intensité du courant est supérieure ou égale à 80 mA. 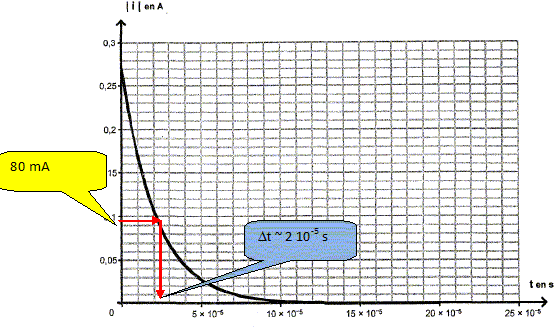A l'aide du graphe ci-dessous, expliquer pourquoi le condensateur ne convient pas. La lampe permet de s'éclairer durant environ 20 µs, valeur bien inférieure à 3 min. Etude théorique de la décharge d'un super condensateur. Aspect énergétique. Donner l'expression de l'énergie stockée dans un condensateur puis calculer sa valeur si C' = 1,0 F chargé sous une tension uC = 6,0 V. E = ½C' uC2 = 0,50 * 6,02 = 18 J. Comparer cette valeur avec celle de l'énergie stoockée dans le condensateur de capacité C = 1,0 µF. E = ½C uC2 = 0,50 10-6* * 6,02 = 18 10-6 J. Le rapport entre les deux énergies est 106, en faveur du super condensateur. Etude de la décharge du super condensateur dans la lampe. Quelle est la relation entre uR et uC ? Etablir l'équation différentielle vérifiée par la tension uC. uR + uC = 0. uR = Ri avec i = dq/dt ; de plus q = C uC avec C une constante. D'où i = CduC/dt et RCduC/dt + uC = 0. Une solution de cette équation différentielle est du type uC(t) = A exp(-t/t) où A est une constante à déterminer. Déterminer la valeur de A. On écrit qu' à l'instant t=0, la tension aux bornes du condensateur est égale à 6,0 V : 6,0 = A exp(0) ; A = 6,0 V. Montrer que i(t) = -0,27 exp (-t/22). Constante de temps : t = RC = 22*1,0 = 22 s. De plus i = CduC/dt = 6,0 * 1,0 *(-1 / 22) exp (-t/22). i = -0,27 exp (-t / 22). 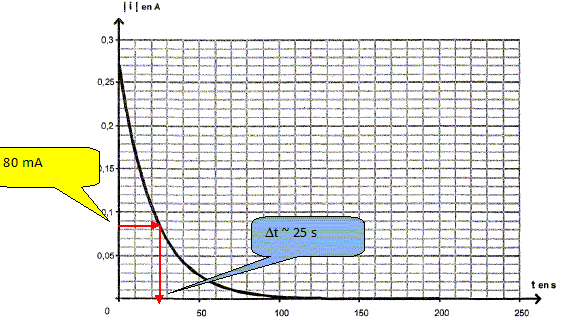Philippe trace la courbe | i | = f(t). Ce super condensateur convient-il ? Justifier. La lampe éclaire correctement pendant environ 25 s, ce qui est encore bien inférieur à 3 minutes. Ce super condensateur ne convient pas.

retour -menu